深入理解softmax函数
一、softmax函数公式
softmax用于多分类过程中,它将多个神经元的输出,映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类。假设我们有一个数组Z,Zi表示Z中的第i个元素,那么这个元素的softmax值就是如下:
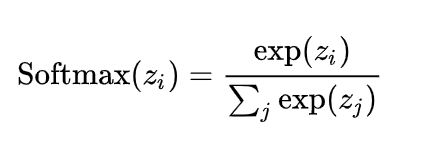

Softmax函数可以将上一层的原始数据进行归一化,转化为一个【0,1】之间的数值,这些数值可以被当做概率分布,用来作为多分类的目标预测值。Softmax函数一般作为神经网络的最后一层,接受来自上一层网络的输入值,然后将其转化为概率。之所以要选用e作为底数的指数函数来转换概率,是因为上一层的输出有正有负,采用指数函数可以将其第一步都变成大于0的值,然后再算概率分布。
二、输入值量级的大小对softmax函数的概率输出有什么影响?
import numpy as np def softmax(x): exp_x = np.exp(x) sum_exp_x = np.sum(exp_x) y = [round(i/sum_exp_x,2) for i in exp_x] return y a0=[0.1,0.2,0.3] print(softmax(a0)) a1=[1,2,3] print(softmax(a1)) a2=[10,20,30] print(softmax(a2)) a3=[100,200,300] print(softmax(a3)) OUT: [0.3, 0.33, 0.37] [0.09, 0.24, 0.67] [0.0, 0.0, 1.0] [0.0, 0.0, 1.0]
从上述例子可以看出来,随着输入元素的量级变大,softmax的值以指数级的速度向最大元素靠近,其它元素的softmax值逐渐变为0。因为虽然10和20看起来没差多少,但是换成指数形式,就相差非常大,所以最大的元素经过softmax变换后就变成主导的因素了,逐渐逼近1,这也是为什么神经网络的最后一层输出都会加一个logit函数的原因,使其变小后再输入softmax函数。还有一个关键问题就是,如果softmax的输出值变成【0,0,1】,在对softmax求导反向传播的时候,其梯度也基本接近0,无法学习。
三、softmax函数的求导
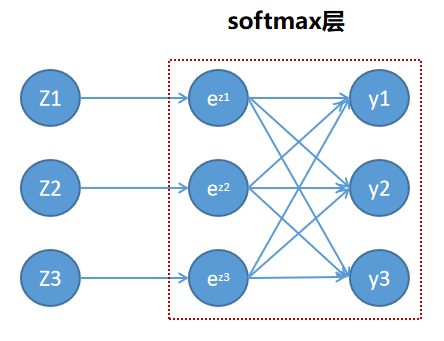

函数相除的求导运算法则:
![]()
①当i=j时,以φy1/φz1为例子:

②当i≠j时,以φy1/φz2为例子:
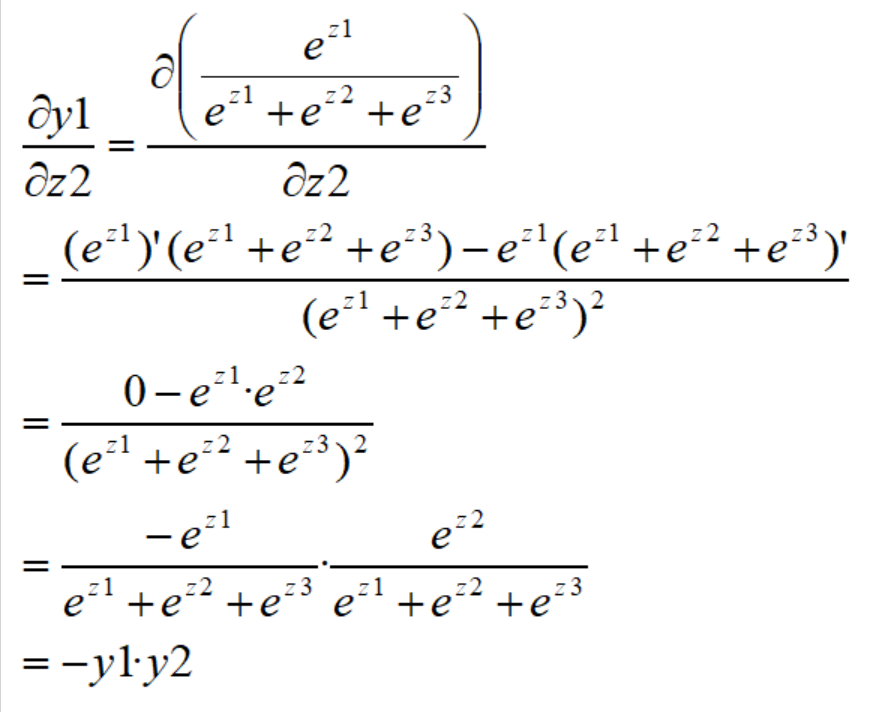
③同理,φy1/φz3
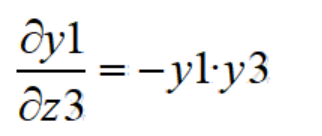
所以,对于Softmax函数的梯度推导依然使用的是导数的基本运算,最终表达式如下:
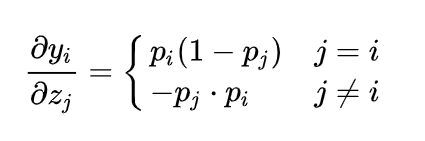
所以,当softmax后的元素值分布如【0,0,1】或者为【0.005,0.005,0.99】的时候,在反向传播的时候,梯度基本等于0,参数基本没法更新,模型无法进一步学习
参考文献:https://zhuanlan.zhihu.com/p/105722023


