大幅减少GPU显存占用:可逆残差网络(The Reversible Residual Network)
前序:
Google AI最新出品的论文Reformer 在ICLR 2020会议上获得高分,论文中对当前暴热的Transformer做两点革新:一个是局部敏感哈希(LSH);一个是可逆残差网络代替标准残差网络。本文主要介绍变革的第二部分,可逆残差网络。先从神经网络的反向传播讲起,然后是标准残差网络,最后自然过渡到可逆残差网络。读完本文相信你会对神经网络的架构发展有一个非常清晰的认识。
一、背景介绍
当前所有的神经网络都采用反向传播的方式来训练,反向传播算法需要存储网络的中间结果来计算梯度,而且其对内存的消耗与网络单元数成正比。这也就意味着,网络越深越广,对内存的消耗越大,这将成为很多应用的瓶颈。由于GPU的显存受限,使得网络结构难以达到最优,因为有些网络结构可能达到上千层的深度。如果采用并行GPU的话,价格既昂贵又比较复杂,同时也不适合个人研究。

上面是torchsummary截图,forword和bacword pass size就是需要保存的中间变量大小,可以看出这部分占据了大部分显存。如果不存储中间层结果,那么就可以大幅减少GPU的显存占用,有助于训练更深更广的网络。多伦多大学的Aidan N.Gomez和Mengye Ren提出了可逆残差神经网络,当前层的激活结果可由下一层的结果计算得出,也就是如果我们知道网络层最后的结果,就可以反推前面每一层的中间结果。这样我们只需要存储网络的参数和最后一层的结果即可,激活结果的存储与网络的深度无关了,将大幅减少显存占用。令人惊讶的是,实验结果显示,可逆残差网络的表现并没有显著下降,与之前的标准残差网络实验结果基本旗鼓相当。
如果你已经对很多计算细节遗忘不清楚了,没关系,下面我们将先从BP反向传播、标准残差网络一步步讲起,本文的目的就是要带你从头到尾搞清楚。首先我们温故一下多元复合函数求导公式:
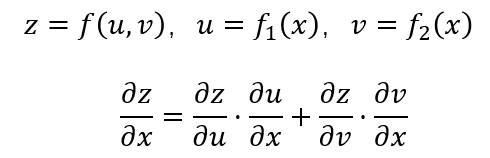
二、神经网络的反向传播(BP)
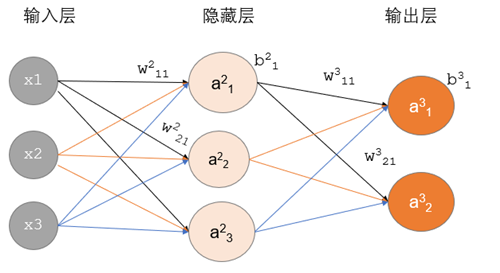
符号表示:
X1,X2,X3:表示3个输入层节点
Wtji:表示从t-1层到t层的权重参数,j表示t层的第j个节点,i表示t-1层的第i个节点
ati:表示t层的第i个激活后输出结果
g(x):表示激活函数
正向传播计算过程:
<隐藏层>
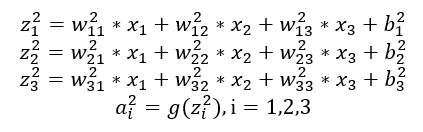
<输出层>
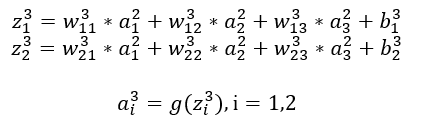
反向传播:
以单个样本为例,假设输入向量是[x1,x2,x3],目标输出值是[y1,y2],代价函数用L表示。反向传播的总体原理就是根据总体输出误差,反向传播回网络,通过计算每一层节点的梯度,利用梯度下降法原理,更新每一层的网络权重w和偏置b,这也是网络学习的过程。误差反向传播的优点就是可以把繁杂的导数计算以数列递推的形式来表示, 简化了计算过程。
以平方误差来计算反向传播的过程,代价函数表示如下:

根据导数的链式法则反向求解隐藏->输出层、输入层->隐藏层的权重表示:
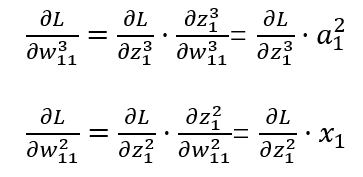
引入新的误差求导表示形式,称为神经单元误差:
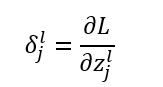
l=2,3表示第几层,j表示某一层的第几个节点。替换表示后如下:

所以我们可以归纳出一般的计算公式:
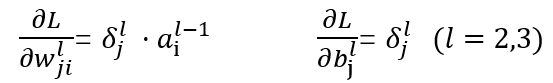
从上述公式可以看出,如果神经单元误差δ可以求出来,那么总误差对每一层的权重w和偏置b的偏导数就可以求出来,接下来就可以利用梯度下降法来优化参数了。
求解每一层的δ:
输出层

隐藏层
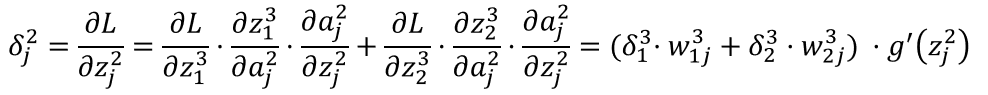
也就是说,我们根据输出层的神经误差单元δ就可以直接求出隐藏层的神经误差单元,进而省去了隐藏层的繁杂的求导过程,我们可以得出更一般的计算过程:
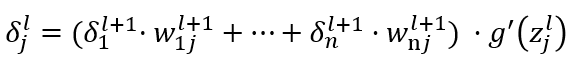
从而得出l层神经单元误差和l+1层神经单元误差的关系。这就是误差反向传播算法,只要求出输出层的神经单元误差,其它层的神经单元误差就不需要计算偏导数了,而可以直接通过上述公式得出。
三、残差网络(Residual Network)
残差网络主要可以解决两个问题:1)梯度消失问题;2)网络退化问题。其结构如下图
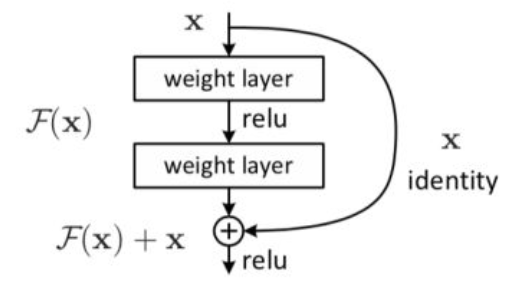
上述结构就是一个两层网络组成的残差块,残差块可以由2、3层甚至更多层组成,但是如果是一层的,就变成线性变换了,没什么意义了。上述图可以写成公式如下:
F(x)=W2 * ReLU(W1 * X)
所以在第二层进入激活函数ReLU之前F(x)+X组成新的输入,也叫恒等映射,就是在这个残差块输入是X的情况下输出依然是X,这样其目标就是学习让F(X)=0。
为什么要额外加一个X呢,而不是让模型直接学习F(x)=X?
因为让F(x)=0比较容易,初始化参数W非常小接近0,就可以让输出接近0,同时输出如果是负数,经过第一层Relu后输出依然0,都能使得最后的F(X)=0,也就是有多种情况都可以使得F(x)=0;但是让F(x)=x确实非常难的,因为参数都必须刚刚好才能使得最后输出为X。
恒等映射有什么作用?
恒等映射就可以解决网络退化的问题,当网络层数越来越深的时候,网络的精度却在下降,也就是说网络自身存在一个最优的层度结构,太深太浅都能使得模型精度下降。有了恒等映射存在,网络就能够自己学习到哪些层是冗余的,就可以无损通过这些层,理论上讲再深的网络都不影响其精度,解决了网络退化问题。
为什么可以解决梯度消失问题呢?
以两个残差块的结构实例图来分析,其中每个残差块有2层神经网络组成,如下图:

假设激活函数ReLU用g(x)函数来表示,样本实例是[X1,Y1],即输入是X1,目标值是Y1,损失函数还是采用平方损失函数,则每一层的计算如下:
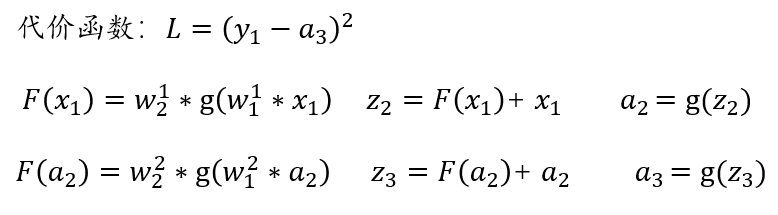
下面我们对第一个残差块的权重参数求导,根据链式求导法则,公式如下:

我们可以看到求导公式中多了一个+1项,这就将原来的链式求导中的连乘变成了连加状态,可以有效避免梯度消失了。
四、可逆残差网络(Reversible Residual Network)
1)可逆块结构
可逆神经网络将每一层分割成两部分,分别为x1和x2,每一个可逆块的输入是(x1,x2),输出是(y1,y2)。其结构如下:
正向计算图示:

公式表示:
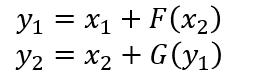
逆向计算图示:
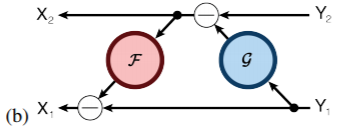
公式表示:
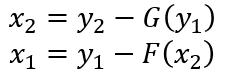
其中F和G都是相似的残差函数,参考上图残差网络。可逆块的跨距只能为1,也就是说可逆块必须一个接一个连接,中间不能采用其它网络形式衔接,否则的话就会丢失信息,并且无法可逆计算了,这点与残差块不一样。如果一定要采取跟残差块相似的结构,也就是中间一部分采用普通网络形式衔接,那中间这部分的激活结果就必须显式的存起来。
2)不用存储激活结果的反向传播
为了更好地计算反向传播的步骤,我们修改一下上述正向计算和逆向计算的公式:

尽管z1和y1的值是相同的,但是两个变量在图中却代表不同的节点,所以在反向传播中它们的总体导数是不一样的。Z1的导数包含通过y2产生的间接影响,而y2的导数却不受y2的任何影响。
在反向传播计算流程中,先给出最后一层的激活值(y1,y2)和误差传播的总体导数(dL/dy1,dL/dy2),然后要计算出其输入值(x1,x2)和对应的导数(dL/dx1,dL/dx2),以及残差函数F和G中权重参数的总体导数,求解步骤如下:

3)计算开销
一个N个连接的神经网络,正向计算的理论加乘开销为N,反向传播求导的理论加乘开销为2N(反向求导包含复合函数求导连乘),而可逆网络多一步需要反向计算输入值的操作,所以理论计算开销为4N,比普通网络开销约多出33%左右。但是在实际操作中,正向和反向的计算开销在GPU上差不多,可以都理解为N。那么这样的话,普通网络的整体计算开销为2N,可逆网络的整体开销为3N,也就是多出了约50%。
参考论文:The Reversible Residual Network:Backpropagation Without Storing Activations



