Union-Find 并查集算法
一、动态连通性(Dynamic Connectivity)
Union-Find 算法(中文称并查集算法)是解决动态连通性(Dynamic Conectivity)问题的一种算法。动态连通性是计算机图论中的一种数据结构,动态维护图结构中相连信息。简单的说就是,图中各个节点之间是否相连、如何将两个节点连接,连接后还剩多少个连通分量。有点像我们的微信朋友圈,在社交网络中,彼此熟悉的人之间组成自己的圈子,熟悉之后就会添加好友,加入新的圈子。微信用户有几亿人,如何快速计算任意两个用户是否同属于一个圈子呢?计算机是如何将两个用户连接起来的呢?整个微信用户共有几个独立的圈子呢?Union-Find就可以解决上述问题。
二、基本概念
结合下面图的例子来了解基本概念:
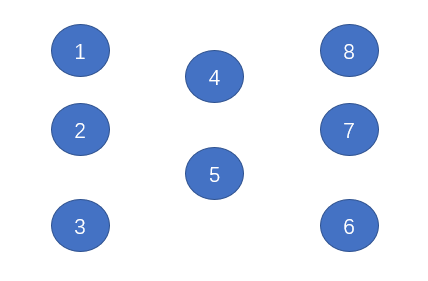
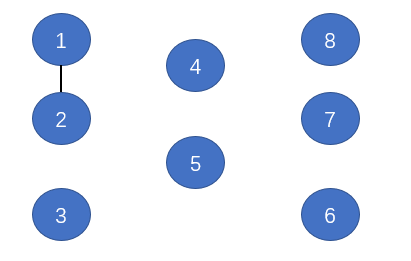
连通是一种等价关系,也就是说具有如下三个性质:
1、自反性:节点p和p是连通的。
2、对称性:如果节点p和q连通,那么q和p也连通。
3、传递性:如果节点p和q连通,q和r连通,那么p和r也连通。
class UF:
def __init__(self,N): #N表示初始化的节点数,也即最初的连通分量数 def union(self,p,q): # 将节点p和q进行连接 def connected(self,p,q): #判断p和q是否连接 def count(): #返回当前的连通分量
除了社交网络中的朋友圈计算,还可以判断编译器同一个变量的不同引用。
Union-Find 算法的关键就在于union和connected函数的效率。使用什么样的数据结构来实现这种高效率呢?
三、解决思路
用树来表示节点直接的连接,只要是连接的节点都在同一颗树中,多棵树就是多个连通分量,进而组成了整个森林。怎么用森林来表示连通性呢?我们设定树的每个节点都有一个指针指向其父节点,如果是根节点的话,这个指针指向自己。
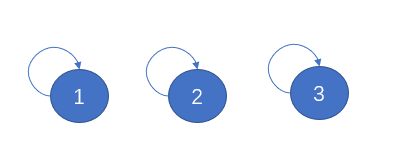
如果某两个节点被连通,则让其中的(任意)一个节点的根节点接到另一个节点的根节点上,这样,如果节点p和q连通的话,它们一定拥有相同的根节点:
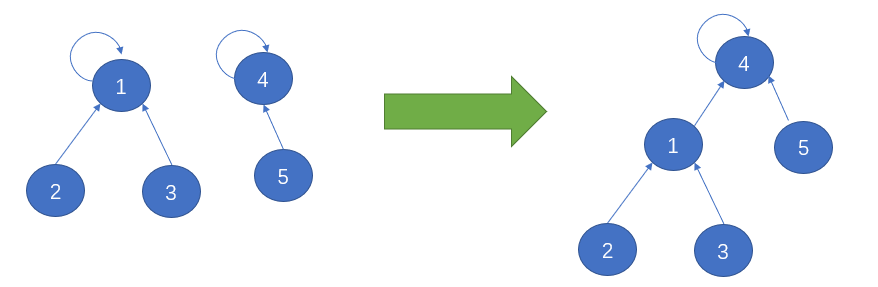
class UF: def __init__(self,N): #N表示初始化的节点数,也即最初的连通分量数 self.count=N self.root=[0] #root表示存储每个节点的根节点,第一个位置用0占位 for i in range(1,N+1): #初始化每个节点的根节点指向自己 self.root.append(i) def union(self,p,q): # 将节点p和q进行连接,让p的根节点指向q节点的根节点即可 if self.connected(p,q): return; p_root=self.find(p) q_root=self.find(q) self.root[p_root]=q_root self.count-=1 def find(self,p): #查找节点p的根节点 while p!=self.root[p]: p=self.root[p] return p def connected(self,p,q): #判断p和q是否连接 return self.find(p)=self.find(q) def count(): #返回当前的连通分量 return self.count
算法效率分析:
从上述代码可以看出,union-find算法的效率主要在于find函数上面,因为union和connected两个函数的关键都在查找根节点上面,即find函数。find主要功能就是从某个节点向上遍历到树根,其时间复杂度就是树的高度。我们可能习惯性地认为树的高度就是logN,但这并不一定。logN的高度只存在于平衡二叉树,对于一般的树可能出现极端不平衡的情况,使得树几乎退化成直线链表,树的高度最坏情况下可能变成N,如下图所示:
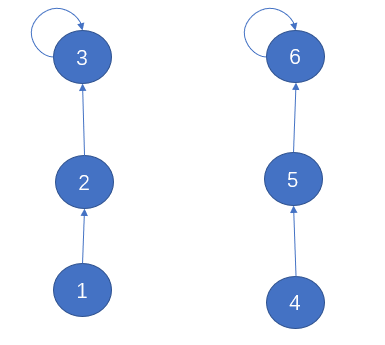
如果按照上面的情况,左边圈子与右边圈子进行连接的话,每个圈子找到根节点的时间复杂度都是O(N)级别的,对于诸如社交网络这样数据规模巨大的问题,而union和connected的调用都非常频繁,每次都需要线性时间复杂度,效率就显得比较低下了。其实这个问题就是树不平衡造成的。
四、平衡树
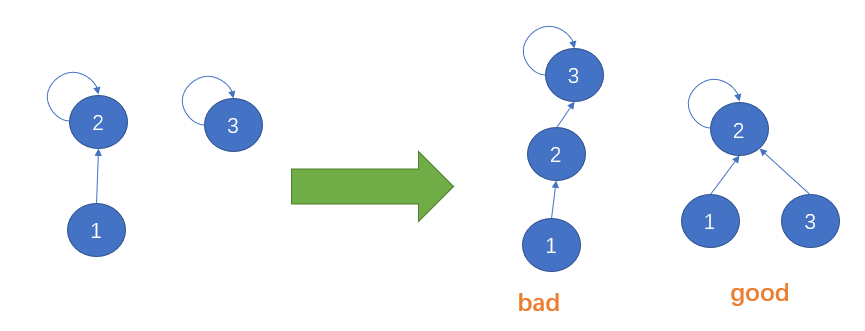
class UF: def __init__(self,N): #N表示初始化的节点数,也即最初的连通分量数 self.count=N self.root=[0] #root表示存储每个节点的根节点,第一个位置用0占位 self.size=[0] for i in range(1,N+1): #初始化每个节点的根节点指向自己,树的大小为1 self.root.append(i) self.size.append(1) def union(self,p,q): # 将节点p和q进行连接,让p的根节点指向q节点的根节点即可 if self.connected(p,q): return; p_root=self.find(p) q_root=self.find(q) if size[p_root]<= size[q_root]: self.root[p_root]=q_root self.size[q_root]+=self.size[p_root] #p节点数合并到q根节点上 else: self.root[q_root]=self.root[p_root] self.size[p_root]=self.size[p_root] #q节点数合并到p根节点上 self.count-=1 def find(self,p): #查找节点p的根节点 while p!=self.root[p]: p=self.root[p] return p def connected(self,p,q): #判断p和q是否连接 return self.find(p)=self.find(q) def count(): #返回当前的连通分量 return self.count
五、路径压缩(进一步优化find函数)
是不是可以进一步压缩树的高度,加快find函数的查找速度,find的效率提升了,等于union和connected函数效率提升了。

如果是上图这种形式,那查找速度基本就是O(1)级别了。但是一个平衡树一步是不可能压缩到这种形式,可以在find函数中加上一行代码,在每次查找的时候,就可以顺便压缩了路径,将树的高度进一步降低,代码如下:
class UF: def __init__(self,N): #N表示初始化的节点数,也即最初的连通分量数 self.count=N self.root=[0] #root表示存储每个节点的根节点,第一个位置用0占位 self.size=[0] for i in range(1,N+1): #初始化每个节点的根节点指向自己,树的大小为1 self.root.append(i) self.size.append(1) def union(self,p,q): # 将节点p和q进行连接,让p的根节点指向q节点的根节点即可 p_root=self.find(p) q_root=self.find(q) if p_root==q_root: return if self.size[p_root]<= self.size[q_root]: self.root[p_root]=q_root self.size[q_root]+=self.size[p_root] #p节点数合并到q根节点上 else: self.root[q_root]=self.root[p_root] self.size[p_root]=self.size[p_root] #q节点数合并到p根节点上 self.count-=1 def find(self,p): #查找节点p的根节点 while p!=self.root[p]: self.root[p]=self.root[self.root[p]]#路径压缩,直接把p节点指向其父节点的父节点,其实查找也变成了跳跃查找了。 p=self.root[p] return p def connected(self,p,q): #判断p和q是否连接 return self.find(p)==self.find(q) def count_func(): #返回当前的连通分量 return self.count
这种思路每调用一次find函数,路径就会压缩一次,直到路径不能压缩为止。
看代码不好理解,我们以图示的形式进行展示:




