PCA主成分分析理解

一、理论概述

1）问题引出

先看如下几张图：

　　从上述图中可以看出，如果将3个图的数据点投影到x1轴上，图1的数据离散度最高，图3其次，图2最小。数据离散性越大，代表数据在所投影的维度上具有越高的区分度，这个区分度就是信息量。如果我们用方差来形容数据的离散性的话，就是数据方差越大，表示数据的区分度越高，也就是蕴含的信息量是越大的。

　　基于这个知识，如果对数据进行降维的话，图1投影到x1轴上面，数据的离散度最大；图2投影到x2轴上离散度最大，图3呢？图3需要找到一个新的坐标轴，使其投影到上面的数据方差最大，如下图所示：

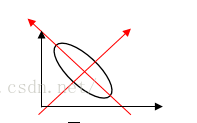
从上面图中可以看出，在新的坐标轴上进行投影的话，图3可以选择一个离散度最大的轴进行投影，在尽量保留最多信息量的情况下，进行了数据降维。

 

如何找到这样的坐标轴呢？

经过数学上的推导的可以知道，特征值对应的特征向量就是理想中想取得正确的坐标轴，而特征值就等于数据在旋转之后的坐标上对应维度上的方差。也就是说，直接求出矩阵A的特征值及其对应的特征向量，就能找到旋转后正确的坐标轴。例如取前k个最大特征值对应的特征向量作为新轴的话，就是将数据降维到k维空间，特征值描述对应特征向量方向上包含的信息量，前k个特征值之和除以总的特征值之和，就是降维后保留原信息的比例。

 

补充知识：何为一个向量在另外一个向量上的投影？

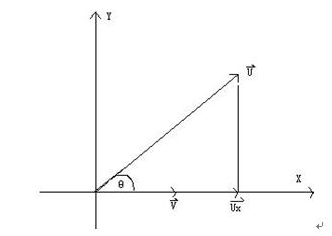
如上图所示，u向量在v向量上的投影就是从u向量向v向量方向上做垂线，其长度就是原点到垂点的距离，方向与v向量方向一致，公式表示如下：

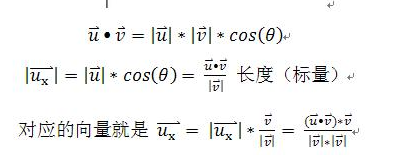
从公式上看，其投影后的长度就等于u的长度乘以cosθ，也就是原点到垂点的距离，向量表示就是v所示方向上的单位向量乘以投影后的长度即可。

2）PCA思想

PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

 

如何得到这些包含最大差异性的主成分方向呢？

通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值与特征向量，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中，实现数据特征的降维。

如上图所示，二维空间中最多可以找到两个特征值与特征向量，注意这里面的特征向量的维度依然跟原数据空间一致，因为还是原数据空间的向量。如果原数据是3维的，则特征向量还是3维的，但是可以找到两个最大的特征值及其对应的特征向量，然后原数据就可以在这两个特征向量所表示的空间上进行映射了，从而将原数据由3维降到2维。

 

如何得到协方差矩阵的特征值特征向量？

PCA算法有两种实现方法：基于特征值分解协方差矩阵实现PCA算法、基于SVD分解协方差矩阵实现PCA算法。

 

二、特征值分解矩阵

 

对于矩阵A，有一组特征向量v，将这组向量进行正交化单位化，就能得到一组正交单位向量。特征值分解，就是将矩阵A分解为如下式：

 

 

其中，Q是矩阵A的特征向量组成的矩阵，则是一个对角阵，对角线上的元素就是特征值，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变换方向（从主要的变化到次要的变化排列）。

具体步骤如下：

输入：数据集X={x1,x2,x3...,xn}，需要降到k维。
1) 去平均值(即去中心化)，即每一位特征减去各自的平均值。、

2) 计算协方差矩阵，最后协方差矩阵可以处以样本数。

3) 用特征值分解方法求协方差矩阵的特征值与特征向量。

4) 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。

5) 将数据转换到k个特征向量构建的新空间中，即Y=PX。

举例如下：

总结：特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多么重要，而特征向量表示这个特征是什么。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

 

三、SVD(Singular Value Decomposition)分解，也叫奇异值分解

利用特征值分解提取特征矩阵是一个容易理解且便于实现的方法。但是为什么还存在奇异值分解呢？特征值分解最大的问题是只能针对方阵，即n*n的矩阵。而在实际的应用中，我们分解的大部分都不是方阵。奇异值分解是一个能适用于任意矩阵的一种分解的方法，对于任意矩阵A总是存在一个奇异值分解：

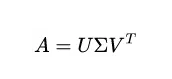
A是m*n的矩阵。

U是m*m的正交矩阵，U里面的正交向量被称为左奇异向量。

Σ是m*n的对角阵，对角线以外的元素都为0，对角线上的元素称为奇异值，奇异值一般从大到小排列。

V^T是n*n的正交矩阵，它是V的转置矩阵，它里面的正交向量被称为右奇异值向量。

 

如何求解左奇异向量、右奇异向量、奇异值呢？

由上面的奇异值分解等式，我们是不知道如何拆分矩阵A的。我们可以把奇异值和特征值联系起来。

首先，我们用矩阵A的转置乘以A，得到一个方阵，用这样的方阵进行特征分解，得到的特征值和特征向量满足下面的等式：

  

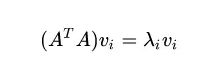
这里的v_i就是我们要求的右奇异向量。

其次，我们将A和A的转置做矩阵的乘法，得到一个方阵，用这样的方阵进行特征分解，得到的特征和特征向量满足下面的等式：

 

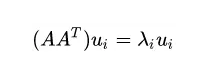
这里的u_i就是左奇异向量。

 

证明如下：

∵  A=UΣV^T          A^T=VΣ^TU^T

∴ A^TA=VΣ^TU^TUΣV^T=VΣ^TΣV^T=VΣ²V^T 

因为V是正交矩阵，所以V^T=V^-1,参考上面（二）特征值分解的公式可知，V就是A^TA的特征向量，奇异值的平方就等于A^TA的特征值。 

 

SVD分解后维度似乎并没有减少，如何应用呢？

在奇异值分解矩阵中Σ里面的奇异值按从大到小的顺序排列，奇异值从大到小的顺序减小的特别快。在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上。也就是说，剩下的90%甚至99%的奇异值几乎没有什么作用。因此，我们可以用前面r个大的奇异值来近似描述矩阵，于是奇异值分解公式可以写成如下：

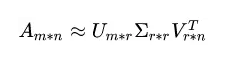
其中r是一个远远小于m和n的数，右边的三个矩阵相乘的结果将会使一个接近A的矩阵。如果r越接近于n，则相乘的结果越接近于A。如果r的取值远远小于n，从计算机内存的角度来说，右边三个矩阵的存储内存要远远小于矩阵A的。所以在奇异值分解中r的取值很重要，就是在计算精度和时间空间之间做选择。

 

SVD的应用：

1)降维。

 通过奇异值分解的公式，我们可以很容易看出来，原来矩阵A的特征有n维。经过SVD分解后，可以用前r个非零奇异值对应的奇异向量表示矩阵A的主要特征，这样就把矩阵A进行了降维。

2)压缩。

通过奇异值分解的公式，我们可以看出来，矩阵A经过SVD分解后，要表示原来的大矩阵A，我们只需要存储U、Σ、V三个较小的矩阵即可。而这三个较小规模的矩阵占用内存上也是远远小于原有矩阵A的，这样SVD分解就起到了压缩的作用。

SVD的优点：

1）有些SVD算法可以不先求协方差矩阵，而直接求出右奇异矩阵V，在样本量很大的情况下非常有效，节省了计算。

2）特征值分解分解方法其实只是用到了SVD中的左奇异矩阵，而没有用到右奇异矩阵。左奇异矩阵可以多行数进行降维（参考特征值分解的例子），右奇异矩阵可以对列数降维，也就是说SVD既可以对函数降维还可以对列数降维。

 

 

参考文献：https://blog.csdn.net/program_developer/article/details/80632779