凸函数与凸优化( 转)

图像:

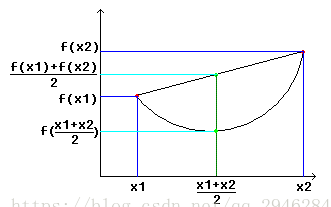
定义： 

设x1x1和x2x2为函数f(x)定义域内的任意两个实数，且x1x1 < t <x2x2,恒有： 

 

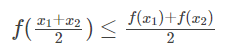
则称f(x) 是定义域上的凸函数。

判定：

凸函数的判定： 
f(x) 在区间[a,b]上连续，在(a,b)内二阶可导，那么： 
一阶判定条件: 设f(x)在凸集S上具有一阶连续偏导数，则f(x)为S上凸函数的充分必要条件是，对S中任意两点x1和x2，恒有： 

 

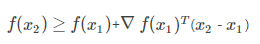
这个函数叫做一阶近似对于函数f。直观地，可以认为是用点x的切线来估计f。通俗说，如果拿我们的函数，在任何点画一条切线，然后在这条线上的每个点对应的函数值，都将小于在函数f上的值，如图所示：

解析上图：点（x,f(x)）是凸函数上对应的点，设切线对应的函数为h(x), 斜率为a，则h(x)=f(x),h(y)=f(x)+a*(y-x) ，因为斜率a=(h(y)-h(x))/(y-x)，跟梯度上升有点像。

 

凸函数的二阶充要条件

 

 

很简单，如果一个函数的二阶导数大于等于零，那么这个函数就是凸函数。图就不上了，很好理解，函数的一阶导数具有递增性，那么函数本身就是凸函数。

 

通过暴力计算法，可以很快地判断函数是不是凸函数。凹函数同理。

 

凸优化：

之所以要区分凸优化问题和非凸的问题原因在于凸优化问题中局部最优解同时也是全局最优解，这个特性使凸优化问题在一定意义上更易于解决，而一般的非凸最优化问题相比之下更难解决。

非凸优化问题如何转化为凸优化问题的方法：
1. 修改目标函数，使之转化为凸函数
2. 抛弃一些约束条件，使新的可行域为凸集并且包含原可行域

原文：https://blog.csdn.net/qq_29462849/article/details/80619913