常见的数据结构总结
写在前面:在我们找工作的过程中,经常会被问到是否了解常见的数据结构,所以,如果想在面试过程中有个良好的表现,对常见的数据结构有一定的了解是必须的。
1 概述
数据结构:指的是相互之间存在一种或多种特定关系的数据元素的集合。
数据结构大致可以分为以下三类:
(1)线性结构:数据元素之间为一对一的关系,常见的有:线性表、队列和栈。
(2)树形结构:数据元素之间为一对多的关系,常见的有:树、堆。
(3)图形结构:数据元素之间为多对多的关系。
2 线性结构
2.1 线性表
线性表是最简单、最基本、最常用的一种数据结构,可以将若干个数据组成的集合看作成一个线性表。
2.1.1 顺序表
顺序表是指用一组地址连续的存储单元依次保存线性表中的数据元素,类似于数组。擅长于快速访问数据,对于增加与删除操作的效率较低。
结构Demo:
typedef struct SeqListType
{
T data[NUM];
int len;
};
2.1.2 链表
链表是采用动态存储分配的一种结构,用一组非连续的存储单元存放数据元素。擅长于增加与删除操作,但对于访问链表中的元素时,效率不高。
结构Demo:
(1)单向链表:
typedef struct Node
{
T data;
struct Node *next;
};
(2)双向链表:
typedef struct Node
{
T data;
struct Node *preview;
struct Node *next;
};
附:对比顺序表与链表
(1)顺序表:
优点:在顺序表中,逻辑上相邻的两个元素在物理位置上也相邻,查找比较方便,存取任一元素的时间复杂度都为O(1)。
缺点:不适合在任意位置插入、删除元素,因为需要移动元素,平均时间复杂度为O(n)。
(2)链表:
优点:在链表的任意位置插入或删除元素只需修改相应指针,不需要移动元素;按需动态分配,不需要按最大需求预先分配一块连续空间。
缺点:查找不方便,查找某一元素需要从头指针出发沿指针域查找,因此平均时间复杂度为O(n)。
2.2 队列
队列是一种特殊的线性表,只允许在表的前端进行删除操作,在表的后端进行插入操作,是一种先进先出(FIFO)的数据结构。
结构Demo:
typedef struct QueueType
{
T data[NUM];
int head;
int tail;
};
注意:为了解决队列的假溢出(即虽然队列前面有空位置,但仍显示队列已满),我们可以将队列的首尾相连,构成一个循环队列。
2.3 栈
栈是线性表的特殊表现形式,按照后进先出(LIFO)的原则处理数据,只能在栈顶进行操作。
栈的基本操作只有两个:
(1)入栈(Push):即将数据保存到栈顶。进行该操作前,先修改栈顶指针,使其向上移一个元素位置,然后将数据保存到栈顶指针所指的位置。
(2)出栈(Pop):即将栈顶的数据弹出,然后修改栈顶指针,使其指向栈中的下一个元素。
结构Demo:
typedef struct StackType
{
T data[NUM];
int top;
};
3 树形结构
树形结构:结点间具有层次关系,每一层的一个结点能且只能和上一层的一个结点相关,但同时可以和下一层的多个结点相关,即:一个结点有一个前驱和多个后继,是一种“一对多”关系,常见类型有:树和堆。
3.1 树
3.1.1 树的基本概念
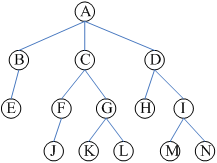
典型的树
(1)父结点、子结点、兄弟结点:A是B、C、D的父结点;B、C、D是A的子结点;B、C、D之间是兄弟结点。
(2)结点的度:一个结点的子树的数量称为该结点的度。例如:A的度为3。
(3)树的度:一棵树的度是指该树中结点的最大度数。例如:本棵树的度为3。
(4)叶结点和分支结点:度为0的结点为叶结点或终端结点,度不为0的结点为分支结点或非终端结点。
(5)结点的层数:A为第1层,B、C、D为第2层。
(6)树的深度:一棵树中结点的最大层数称为树的深度。例如:本棵树的深度为4。
3.1.2 二叉树
1、二叉树:任意结点最多只能有两个子结点,如果只有一个子结点,可以是左子树,也可以是右子树,如下图所示:

2、满二叉树:在二叉树中,除最下一层的叶结点外,每层的结点都有2个子结点,如下图所示:

3、完全二叉树:从根结点到倒数第二层满足满二叉树,最后一层可以不完全填充,但需要保证从左到右的叶结点连续存在,只缺右侧若干结点,如下图所示:
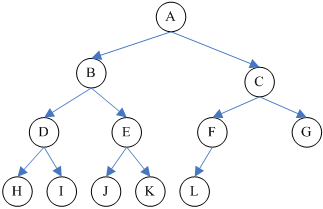
4、二叉树的规律:
(1)在非空二叉树中,第i层的结点总数不超过2i-1;
(2)深度为k的二叉树最多有2k-1个结点,最少有k个结点;
(3)对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1;
(4)具有n个结点的完全二叉树的深度为log2(n)+1;
(5)具有n个结点的完全二叉树各结点如果用顺序方式存储,对任意结点i,有如下关系:
1>、如果i != 1,则其父结点的编号为i/2;
2>、如果2*i<=n,则其左子树根结点的编号为2*i;若2*i>n,则无左子树;
3>、如果2*i+1<=n,则其右子树根结点编号为2*i+1;若2*i+1>n,则无右子树。
5、二叉树的遍历:
D:根节点;L:左子树;R:右子树。
(1)先序遍历:DLR
(2)中序遍历:LDR
(3)后序遍历:LRD
6、最优二叉树(赫夫曼树):
假如一个二叉树有4个叶结点A、B、C、D,权重分别为5、7、2、13,则最优二叉树应该如下所示:
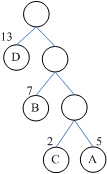
带权路径长度:1*13+2*7+3*2+3*5=48
当我们设置赫夫曼树中左分支代表编码0,右分支代表编码1,如下所示:
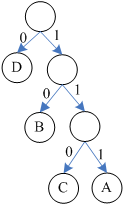
则可进行如下编码(赫夫曼编码):
A:111
B:10
C:110
D:0
3.2 堆
堆是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。
堆总是满足下列性质:
(1)堆中某个节点的值总是不大于或不小于其父节点的值;
(2)堆总是一棵完全二叉树。
4 图形结构
在图形结构中,允许多个结点之间相互关联,称为“多对多”关系,可分为有向图和无向图。
后记:欢迎各路大神批评与指正!



