红黑树的删除调整过程(转载)
首先简单描述一下二叉搜索树的删除过程,可以分为以下四种情况
- 要删除的节点没有左右孩子
- 要删除的节点只有左孩子
- 要删除的节点只有右孩子
- 要删除的节点有左右孩子
对于第一种情况,直接删除。
如果要删除的节点只有左孩子,那么就让该节点的父亲结点指向该节点的左孩子,然后删除该节点,返回true;
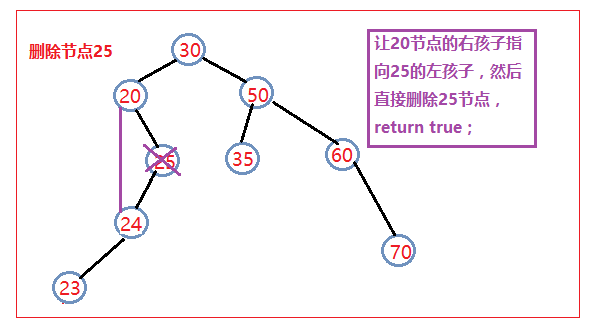
如果要删除的节点只有右孩子,那么就让该节点的父亲结点指向该节点的右孩子,然后删除该节点,返回true;
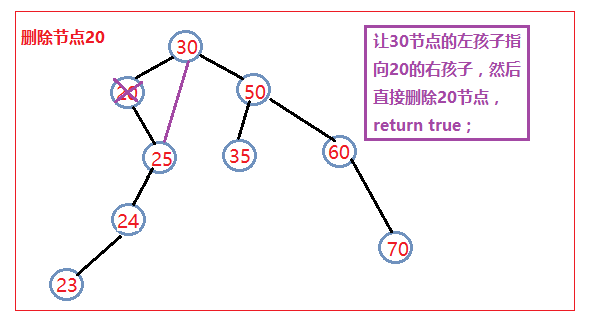
对于上面这两种情况我们还应该在之前进行一个判断,就是判断这个节点是否是根节点,如果是根节点的话,就直接让根节点指向这个节点的左孩子或右孩子,然后删除这个节点。
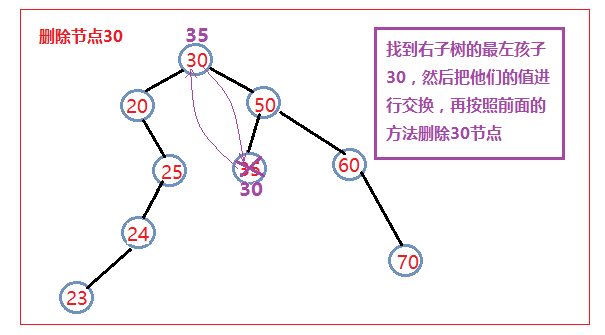
最后一种也是最麻烦的一种就是要删除的节点的左右孩子都存在。此时我们的删除方法如下:
-
找到该节点的右子树中的最左孩子(也就是右子树中序遍历的第一个节点)
-
把它的值和要删除的节点的值进行交换
-
然后删除这个节点即相当于把我们想删除的节点删除了,返回true;
![]()
对于红黑树的删除操作,是在上述操作的基础上对删除节点后的红黑树进行调整。我们按照被删除节点的颜色不同进行讨论。
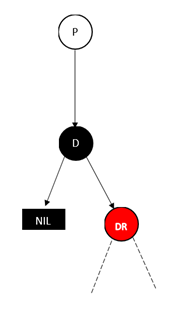
要删除的节点为红色节点
-
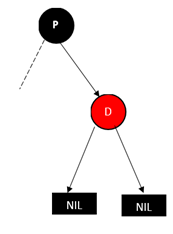
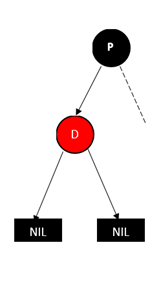
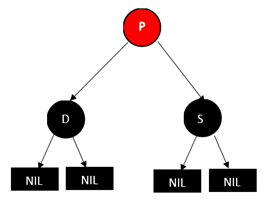
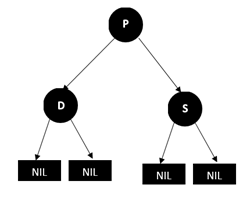
删除红色的叶子节点(D表示待删除的节点,P表示其父亲节点)
![img]()
![img]()
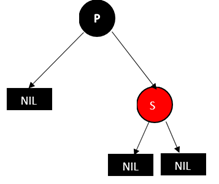
直接删除即可 -
删除红色的非叶节点
只可能出现被删除的节点左右子树都存在的情况,否则违背红黑树的性质。对于这种情况,我们只需要找到被删除节点的直接后继,用它的值取代被删除节点的值,然后按情况1删除。
要删除的节点为黑色节点
-
删除黑色的叶子节点
情况1:待删除节点D的兄弟节点S为红色
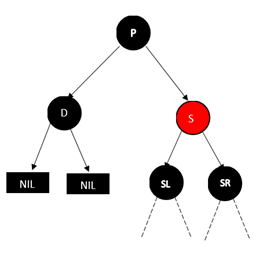
D是左节点的情况
![img]()
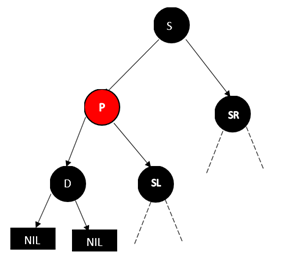
调整做法是将父亲节点和兄弟节点的颜色互换,也就是p变成红色,S变成黑色,然后将P树进行AVL树种的RR型操作,结果如下图
![img]()
这个时候我们会发现,D的兄弟节点变成了黑色,这样就成后面要讨论的情况。
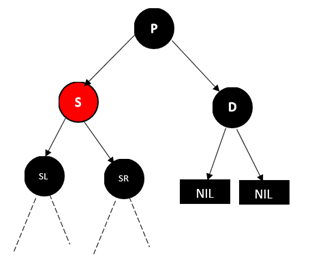
D是右节点的情况
![img]()
将P和S的颜色互换,也就是将P变成红色,将S变成黑色,然后对P进行类似AVL树的LL操作。结果如下图:
![img]()
此时D的兄弟节点变成了黑色,这样就成了我们后面要讨论的情况
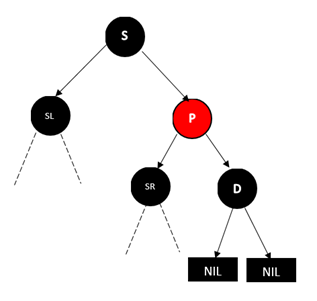
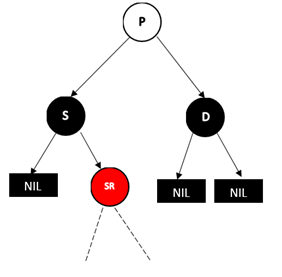
情况2:兄弟节点为黑色,且远侄子节点为红色。
D为左孩子对的情况,这时D的远侄子节点为S****的右孩子
![img]()
没有上色的节点表示黑色红色均可,注意如果SL为黑色,则SL必为NULL节点。
这个时候,如果我们删除D,这样经过D的子节点(NULL节点)的路径的黑色节点个数就会减1,但是我们看到S的孩子中有红色的节点,如果我们能把这棵红色的节点移动到左侧,并把它改成黑色,那么就满足要求了,这也是为什么P的颜色无关,因为调整过程只在P整棵子树的内部进行。
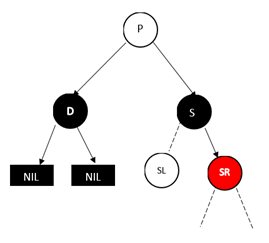
调整过程为,将P和S的颜色对调,然后对P树进行类似AVL树RR型的操作,最后把SR节点变成黑色,并删除D即可。
![img]()
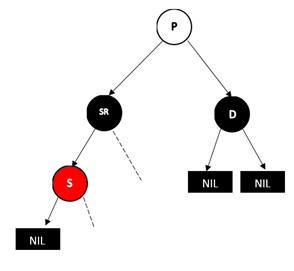
D为右孩子的情况,此时D的远侄子为S****的左孩子
![img]()
同样,将P和S的颜色对调,然后再对P树进行类似AVL树RL型的操作,最后将SR变成黑色,并删掉D即可。结果如下图:
![img]()
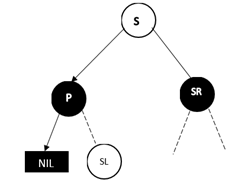
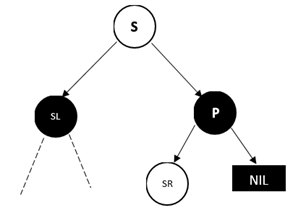
情况3:兄弟节点S为黑色,远侄子节点为黑色,近侄子节点为红色
D为左孩子的情况,此时近侄子节点为S****的左孩子
![img]()
做法是,将SL右旋,并将S和SL的颜色互换,这个时候就变成了情况4。
![img]()
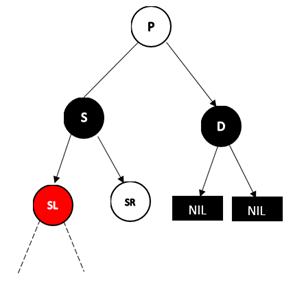
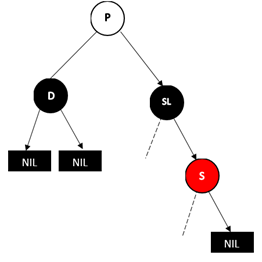
D为右孩子的情况,此时近侄子节点为S****的右孩子
![img]()
做法是将S和SR颜色对调,然后对SR进行左旋操作,这样就变成了情况4,结果如下图:
![img]()
情况4:父亲节p为红色,兄弟节点和兄弟节点的两个孩子(只能是NULL节点)都为黑色的情况。
![img]()
如果删除D,那经过P到D的子节点NULL的路径上黑色就少了一个,这个时候我们可以把P变成黑色,这样删除D后经过D子节点(NULL节点)路径上的黑色节点就和原来一样了。但是这样会导致经过S的子节点(NULL节点)的路径上的黑色节点数增加一个,所以这个时候可以再将S节点变成红色,这样路径上的黑色节点数就和原来一样啦!
所以做法是,将父亲节点P改成黑色,将兄弟节点S改成红色,然后删除D即可。如下图:
![img]()
情况5:父亲节点p,兄弟节点s和兄弟节点的两个孩子(只能为NULL节点)都为黑色的情况
![img]()
方法是将兄弟节点S的颜色改成红色,这样删除D后P的左右两支的黑节点数就相等了,但是经过P的路径上的黑色节点数会少1,这个时候,我们再以P为起始点,继续根据情况进行平衡操作(这句话的意思就是把P当成D(只是不要再删除P了),再看是那种情况,再进行对应的调整,这样一直向上,直到新的起始点为根节点)。结果如下图:
-
删除黑色的非叶节点
-
删除的黑色节点左右子树都存在
首先找到被删除元素D的直接后继,用直接后继的值替换D的值,再对直接后继进行删除。我们可以知道,直接后继是不可能左右子树都存在的,这样就可以将左右子树都存在的情况转化为下面的情况。
-
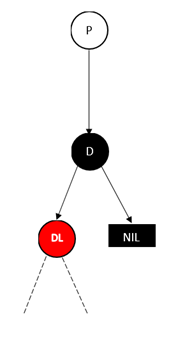
删除的黑色节点仅有左子树或者仅有右子树。
在红黑树中只存在下面这几种情况,其中黑色的竖线代替了左右分支的情况
![img]()
![img]()
-
这两种的处理方式是一样的,即用D的左孩子或者右孩子替换D,并DR的颜色改成黑色即可。
转载自:https://www.cnblogs.com/qingergege/p/7351659.html,https://www.cnblogs.com/MrListening/p/5782752.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号