红黑树的插入调整过程(转载)
红黑树的特性:
红黑树中的每个结点包含五个域:color、key、left、right和parent。如果某结点没有一个子结点或父结点,则该结点相应的指针parent域包含值为NIL(NIL并不是空指针,后面会讲到)。把NIL视为指向红黑树的外结点(叶子)的指针,而把带关键字的结点视为红黑树的内结点。红黑树结点结构如下所示:
- 每个节点或为红色或为黑色。
- 根节点是黑色。
- 每个叶子节点(NIL)是黑色。
- 如果一个节点是候色,那么它的两个儿子都是黑色。
- 对每个节点,从该节点到其孙子结点的所有路径上包含相同数目的黑色节点。
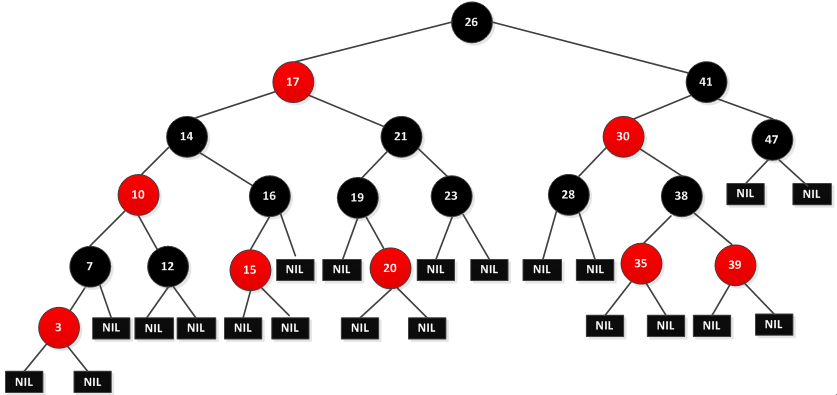
如下图是一棵红黑树:
旋转
在红黑树上进行结点插入和删除操作时,会改变树的结构形状,导致结果可能不满足了红黑树的某些性质,为了保证每次插入和删除操作后,仍然能报维持红黑树的性质,需要改变树中某些结点的颜色和指针结构。其中的指针结构的改变通过旋转完成的。书中给出了两种旋转:左旋转和右旋转。如下图是旋转过程:
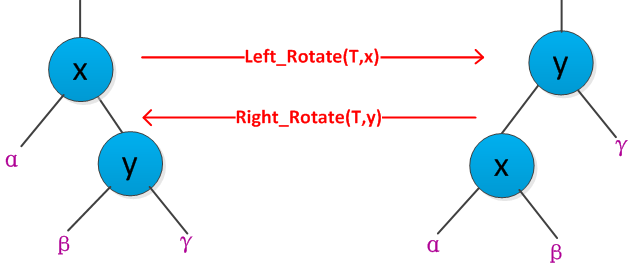
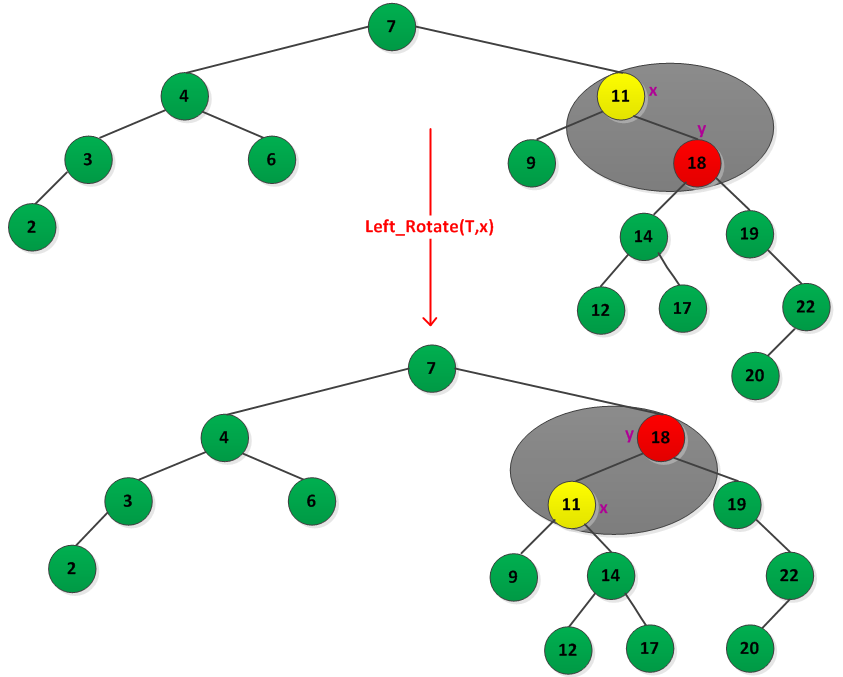
从图可以得出左右旋转的过程,假设对某个结点x进行左旋转,y是x的右孩子,则左旋转过程为:以x和y之间的链为“支轴”进行的,使得x的右孩子为y的左孩子,y的父节点为x的父节点,y的左孩子为x。假设对某个结点y进行右旋转,x是y的左孩子,则右旋转过程为:y的左孩子设置为x的右孩子,将x的父节点设置为y的父节点,x的右孩子设置为y。左旋转的实例如下:
插入
红黑树插入一个新节点z的过程是在二叉查找树插入过程的基础上改进的,先按照二叉排序找到插入位置,将插入节点设为红色,再对插入节点后的结构进行重新着色,使得满足红黑树的性质。
如果每次插入新的节点导致红黑树的性质被破坏,那么不是性质2就是性质4。违反性质2是因为插入节点是根且为红色,违反性质4是因为插入节点和其父节点都是红色。
违反性质4的情况可以给出下面三种可能:
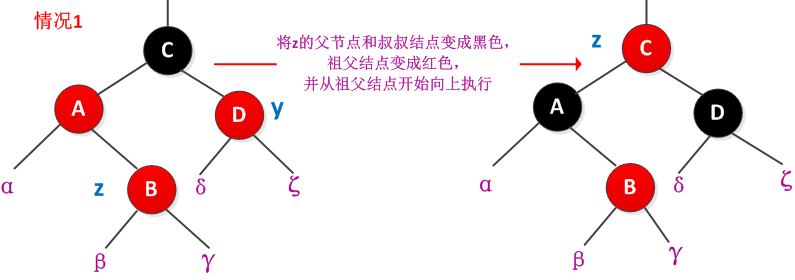
情况1:z的叔叔节点y是红色的
此时z的父节点和y都是红色的,解决办法是将z的父节点]和叔叔结点y都着为黑色,而将z的祖父结点着为红色,然后从祖父结点继续向上判断是否破坏红黑树的性质。处理过程如下图所示:
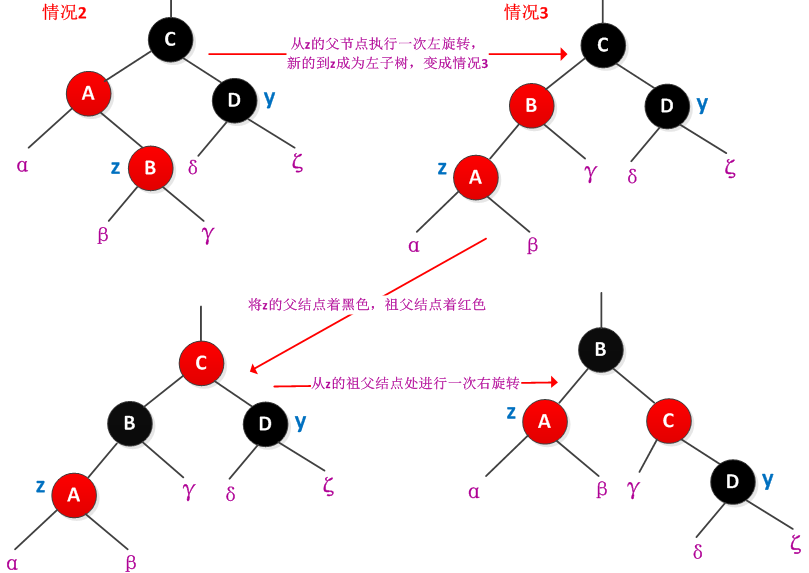
情况2:z的叔叔y是黑色的,而且z是右孩子
情况3:z的叔叔y是黑色的,而且z是左孩子
情况2和情况3中y都是黑色的,通过z是左孩子还是右孩子进行区分的。可以将情况2通过旋转为情况3。情况2中z是右孩子,旋转后成为情况3,使得z变为左孩子,可以在parent[z]结点出使用一次左旋转来完成。无论是间接还是直接的通过情况2进入到情况3,z的叔叔y总是黑色的。在情况3中,将parent[z]着为黑色,parent[parent[z]]着为红色,然后从parent[parent[z]]处进行一次右旋转。情况2、3修正了对性质4的违反,修正过程不会导致其他的红黑性质被破坏。修正过程如下图所示:
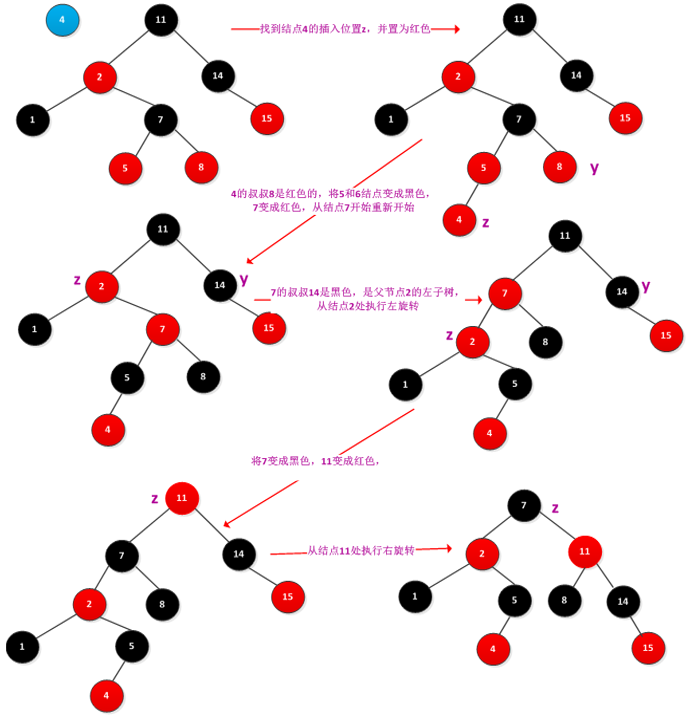
给一个完整的例子来说明插入过程,如下图所示:
转载自:https://www.cnblogs.com/Anker/archive/2013/01/30/2882773.html



