AVL树旋转操作的C++实现(转载)

AVL树的介绍
AVL树是高度平衡的而二叉树。它的特点是：AVL树中任何节点的两个子树的高度最大差别为1。

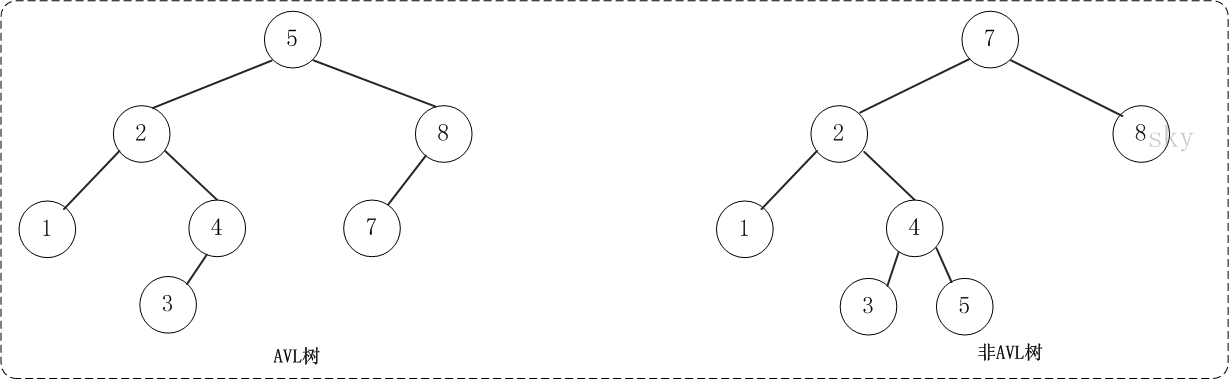
AVL树的C++实现

1. AVL树节点

   template <class T>
   class AVLTreeNode{
       public:
           T key;                //关键字(键值)
           int height;           //高度
           AVLTreeNode *left;    //左孩子
           AVLTreeNode *right;   //右孩子
   
           AVLTreeNode(T value, AVLTreeNode *l, AVLTreeNode *r):
               key(value), height(0),left(l),right(r) {}
   };
   

2. 旋转

   如果在AVL树中进行插入或者删除节点，可能导致AVL树失去了平衡。这种失衡可以概括为以下四种状态:
   

   • LL：LeftLeft，也称为"左左"。插入或删除一个节点后，根节点的左子树的左子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。

     LL失去平衡的情况可以通过一次旋转让AVL树恢复平衡。如下图：

     

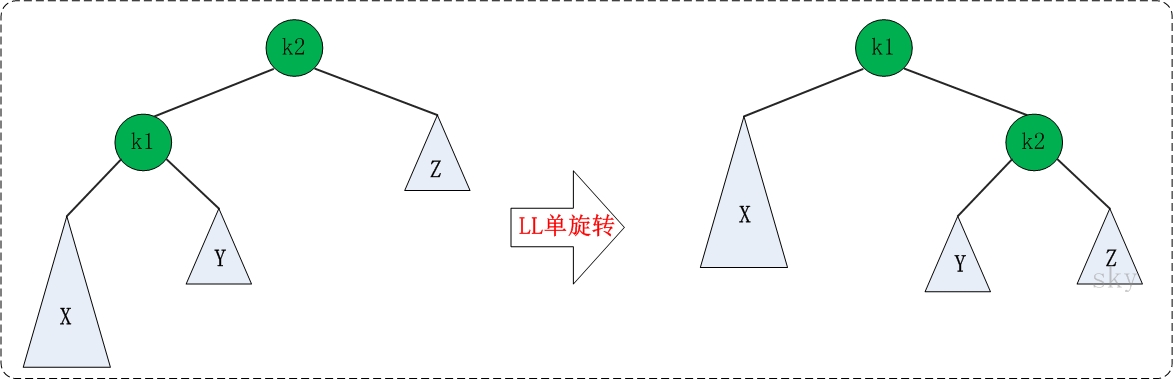
     template <class T>
     AVLTreeNode<T>* LeftLeftRotation(AVLTreeNode<T>* k2)
     {
         AVLTreeNode<T>* k1;
     
         k1 = k2->left; 
         k2->left = k1->right; //k1的右子树成为k2的左子树
         k1->right = k2;       //k2成为k1的右子树
     
         k2->height = max( height(k2->left), height(k2->right)) + 1;
         k1->height = max( height(k1->left), k2->height) + 1;
     
         return k1; //返回旋转后的根节点
     }
     

   • RR：RightRight，称为"右右"。插入或删除一个节点后，根节点的右子树的右子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。

     RR可以看作LL的对称情况：

     

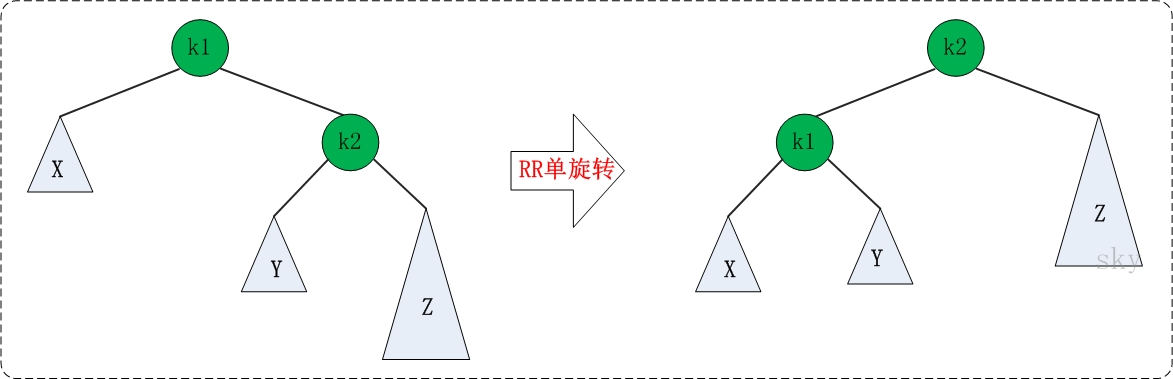
     template <class T>
     AVLTreeNode<T>* RightRightRotation(AVLTreeNode<T>* k1)
     {
         AVLTreeNode<T>* k2;
     
         k2 = k1->right; 
         k1->right = k2->left; //k2的左子树成为k1的右子树
         k2->left = k1;        //k2成为k2的左子树
     
         k1->height = max( height(k1->left), height(k1->right)) + 1;
         k2->height = max( height(k2->right), k1->height) + 1;
     
         return k2; //返回旋转后的根节点
     }
     

   • RL：RightLeft，称为"右左"。插入或删除一个节点后，根节点的右子树的左子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。

     RL需要进行两次旋转才能让AVL树恢复平衡，如下图:

     

     template <class T>
     AVLTreeNode<T>* RightLeftRotation(AVLTreeNode<T>* k1)
     {
         k1->right = LeftLeftRotation(k1->right); //对k3进行LL旋转
         return RightRightRotation(k1); //对k1进行RR旋转
     }
     

   • LR：LeftRight，也称为"左右"。插入或删除一个节点后，根节点的左子树的右子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。

     LR可以看作RL的对称情况，恢复平衡的方法如下：

     

     template <class T>
     AVLTreeNode<T>* LeftRightRotation(AVLTreeNode<T>* k3)
     {
         k3->left = RightRightRotation(k3->left); //对k1进行RR旋转
         return LeftLeftRotation(k3);             //对k3进行LL旋转
     }
     

转载自：http://www.cnblogs.com/skywang12345/p/3577360.html