"蔚来杯"2022牛客暑期多校训练营1部分题题解
感觉自己最近的状态不太对,每场都摆烂.....
得赶紧调整过来,摆烂久了成习惯就不太秒了...
A Villages: Landlines
考虑所有能放电站的地方我们都放,问题就转化成了一个若干个区间联通的问题,我们把所有区间按左端点排序,扫一遍即可。
I Chiitoitsu
刚看到麻将的图片以为是一个麻将的模拟题,没想到读完题后,才发现是个求期望的题目。
求期望还是DP稳啊...我们设f[i][j]表示手上又i张单牌,牌库里又j张牌时,我们最终获胜的期望次数。转移也很显然易见.
正解
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int P=1e9+7;
ll f[20][300];
char c[110];
map<pair<char,char>,int>mp;
inline ll power(ll x,ll y)
{
ll ans=1;
while(y)
{
if(y&1) ans=ans*x%P;
y>>=1;
x=x*x%P;
}
return ans%P;
}
int main()
{
// freopen("1.in","r",stdin);
for(int i=1;i<=13;++i)
{
for(int j=3*i;j<=123;++j)
{
if(i==1) f[i][j]=(1+f[i][j-1]*(j-3*i)%P*power(j,P-2)%P)%P;
else f[i][j]=(1+f[i-2][j-1]*(3*i)%P*power(j,P-2)%P+f[i][j-1]*(j-3*i)%P*power(j,P-2)%P)%P;
}
}
int T;scanf("%d",&T);
for(int os=1;os<=T;++os)
{
scanf("%s",c+1);
mp.clear();
int cnt=13;
for(int i=1;i<=26;i+=2)
{
pair<char,char>pa={c[i],c[i+1]};
mp[pa]++;
if(mp[pa]==2) cnt-=2;
}
printf("Case #%d: %lld\n",os,f[cnt][123]);
}
return 0;
}
J Serval and Essay
像这个题比赛的时候就没来得及看,每次都是被一些题卡住之后,剩下的题就只能弃疗了....
什么时候才能把题一路开过去...
这个题我们按照题意建图,根据题意,我们需要找到一个基本点,把它染成黑色,之后若某个点的所入点都已染黑,则当前点也会被染黑。问最大化黑点的数量。
我们考虑从每个黑点出发,最终扩展的结果一定是一个连着的集合。我们尝试快速迭代出这些集合。倘若一个集合可以被另一个集合所染色,则我们显然让这两个集合合并是更优的。
我们尝试使用启发式合并去做这个事情。
正解
//从一个点出发能够染色的所有点是一个集合.
//我们从每个点都出发,不断的进行染色,扩展它的集合。
//扩展过程中,若一个集合y能够被另一个集合x所染色的话,则显然x能够染色y,我们保留x.
//并将两个集合合并. 最后最大结合即为答案.
//考虑集合合并的话,我们可以采用启发式合并.但还需要考虑将边删除和添加的话,我们考虑
//用set代替vector去做这个事情.
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n,T,f[N],Size[N];
set<int>son[N],fa[N];
inline int getf(int x) {return x==f[x]?x:f[x]=getf(f[x]);}
inline void merge(int x,int y)
{
x=getf(x);y=getf(y);
if(x==y) return;
if(Size[x]<Size[y]) swap(x,y);
f[y]=x;Size[x]+=Size[y];
vector<pair<int,int> >mg;
for(auto v:son[y])
{
son[x].insert(v);
fa[v].erase(y);
fa[v].insert(x);
if(fa[v].size()==1)
mg.push_back({x,v});
}
for(auto u : mg) merge(u.first,u.second);
}
int main()
{
// freopen("1.in","r",stdin);
scanf("%d",&T);
for(int os=1;os<=T;++os)
{
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
son[i].clear();
fa[i].clear();
f[i]=i;Size[i]=1;
}
for(int i=1;i<=n;++i)
{
int k;scanf("%d",&k);
for(int j=1;j<=k;++j)
{
int x;scanf("%d",&x);
son[x].insert(i);
fa[i].insert(x);
}
}
for(int i=1;i<=n;++i)
if(fa[i].size()==1)
merge(*fa[i].begin(),i);
int ans=0;
for(int i=1;i<=n;++i) ans=max(ans,Size[i]);
printf("Case #%d: %d\n",os,ans);
}
return 0;
}
补这个题的时候,这个合并的过程真的是难以理解啊...终于看懂了题解代码,其实只需要维护一个入度集合的正确性即可。
C Grab the Seat!
比赛的时候确实是看这个题了,只是没有细想,边匆匆略过了,并且因为过的人很少,便也没有太去钻研这个题。(充分说明读题的重要性.....)
考虑每个点遮挡的范围,其实是从这个点出发的两个射线的范围,而这两个射线,便是由黑板的两个边界与该点连接而成。
那么总共的遮挡范围便是所有这些角的并集。考虑我们其实只需要最靠里的一个折线段即可。
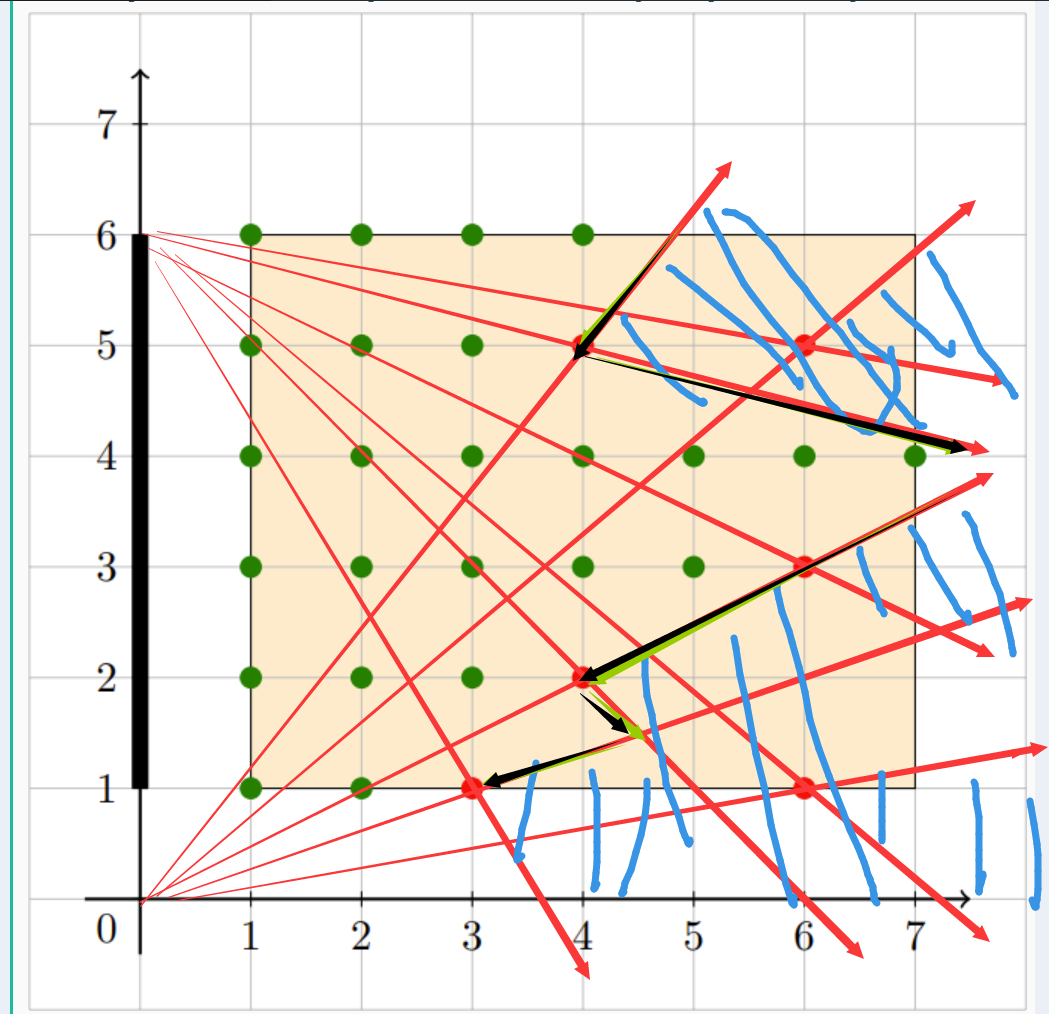
蓝色区域便是每个点的遮挡范围,黑色的便是遮挡的边界了.
我们首先可以将这个折线段分成两类,一类由黑板下端点构成,斜率>0.一类由黑板上端点构成。斜率小于0.
考虑在同一行的两个点,显然,x越小,它所遮挡的范围便越大.并且它所遮挡的范围也包含了比它x大的点的范围。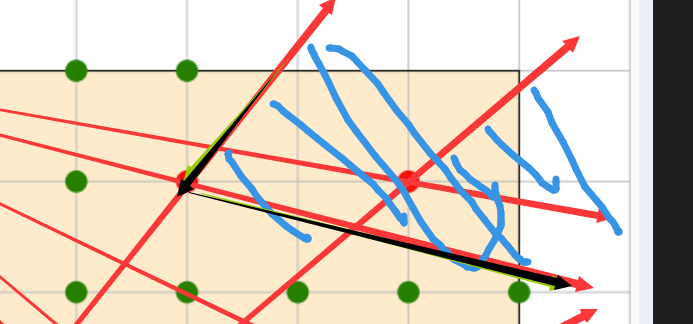
所以说每一行我们只保留最小的x即可。
之后考虑不同行之间我们怎么做取舍。考虑不是当前行的,对当前行的影响(以斜率>0为例)。
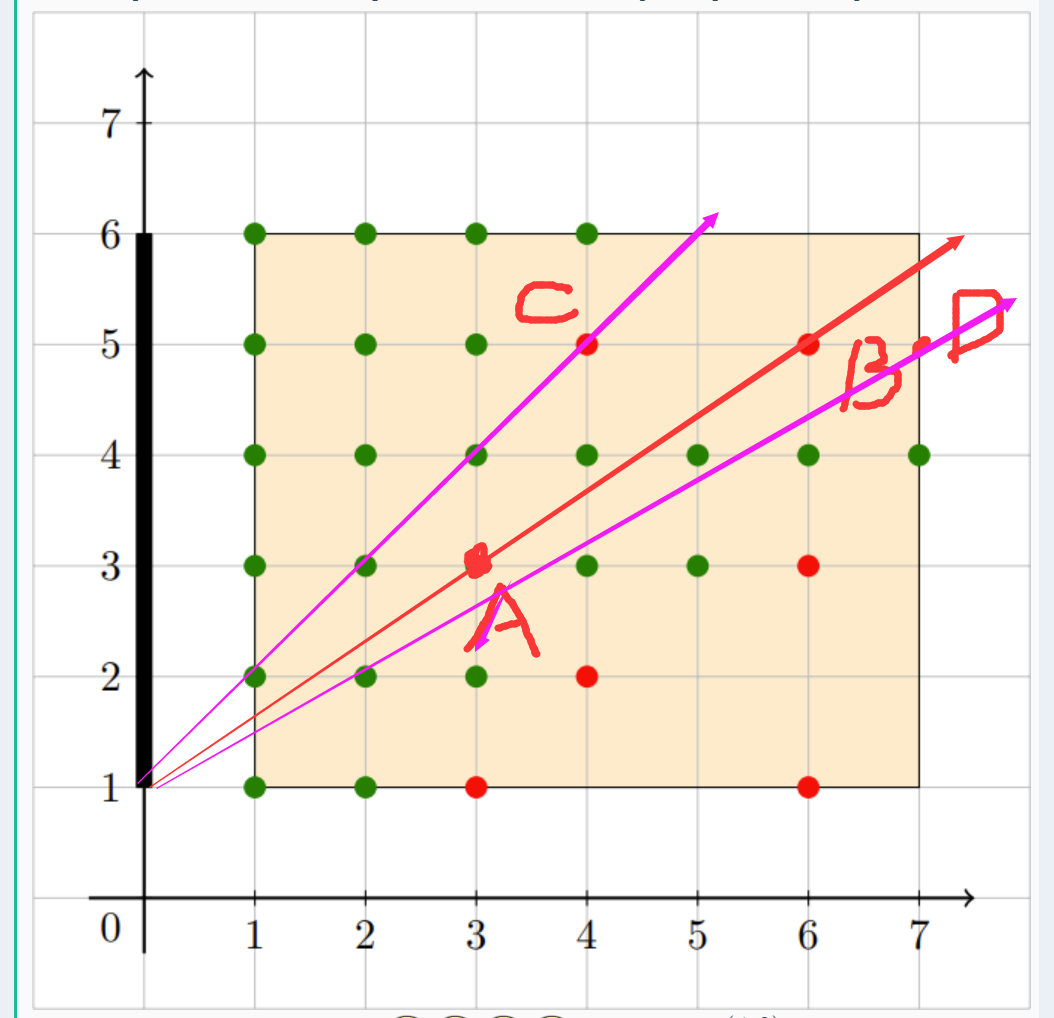
考虑这样的一种情况,在y=5的这一行,我们的边界到底应该由A决定还是由B,C,D决定。显然由C决定,因为C所在的直线在这一行的交点的x值更小。所以说我们每一行的边界是由斜率更大的直线决定的。所以我们y从小到大去枚举这些点,不断维护一个直线的最大斜率,去更新每一行的边界即可。具体看代码。
正解
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+10;
int n,m,k,q;
struct Vector
{
ll x,y;
bool friend operator <(Vector a,Vector b)
{
return a.x*b.y>a.y*b.x;
}
}p[N];
typedef Vector Point;
inline void solve()
{
vector<ll>minn(m+1,n+1),ans(m+1,n+1);//ans[i]表示y=i这一行,第一个被遮挡的点的x
for(int i=1;i<=k;++i) minn[p[i].y]=min(minn[p[i].y],p[i].x);
Vector a={1,0};//保留最大的斜率
for(int i=2;i<=m;++i)
{
a=max(a,Vector({minn[i],i-1}));//保留最大斜率
ans[i]=min(ans[i],(i-1)*a.x/a.y+((i-1)*a.x%a.y!=0));//计算我们保留的直线与当前行的交点
}
a={1,0};
for(int i=m-1;i>=1;--i)
{
a=min(a,Vector({minn[i],i-m}));//保留最小斜率.
ans[i]=min(ans[i],(i-m)*a.x/a.y+((i-m)*a.x%a.y!=0));//计算我们保留的直线与当前行的交点
}
ll re=0;
for(int i=1;i<=m;++i) re+=ans[i]-1;
printf("%lld\n",re);
}
int main()
{
// freopen("1.in","r",stdin);
scanf("%d%d%d%d",&n,&m,&k,&q);
for(int i=1;i<=k;++i) scanf("%d%d",&p[i].x,&p[i].y);
for(int i=1;i<=q;++i)
{
int ps,x,y;
scanf("%d%d%d",&ps,&x,&y);
p[ps]=Point({x,y});
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号