Educational Codeforces Round 113 (Rated for Div. 2)题解
\(A,B,C\)顺利签到,还是在\(D\)上面卡住了,之后在睡前还是想出来了,看来还是自己的思维不够敏捷和成熟...
D. Inconvenient Pairs
简化题意,在一个直角坐标系中,有一些横线和竖线,有一些点,都一定在线上,点只能在线上移动。问:有多少个点对满足他们之间的距离大于他们的曼哈顿距离?
首先我们可以将点分为一下类型,点只在横线上(1),点只在竖线上(2),点既在横线上也在竖线上(3)。我们可以发现第3类型的点到任何点的距离都是曼哈顿距离,所以这种类型的点就不予考虑了。同时,发现,只在横线上的点与只在竖线上的点之间的距离也是曼哈顿距离。那吗符合题意的点对一定是只在横线上的点与只在竖线上的点内部之间的点对。考虑两个点\((x_1,y_1)与(x_2,y_2)(假设x_1<x_2)\)他们是两个只在横线上的点。那么他们之间的距离大于马哈顿的距离的条件是所有竖线的\(x\)值要么\(<x1\),要么\(>x2\).也就是在\(x_1-x_2\)之间没有一条竖线。所以我们只根据横线而言,相邻的两条竖线之间我们就可以统计答案,同时会发现可能多个点会在一条横线上,所以答案统计不能简单的相乘,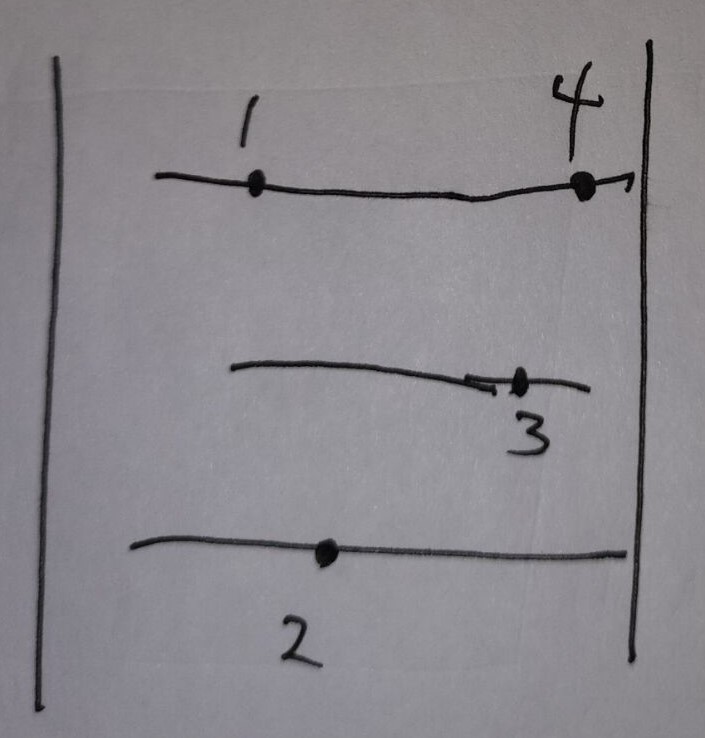
比如这个图:实际上我们不合法的点对应该是\((1,3),(1,2),(4,3)(4,2)(3,2)\),所以我们可以将两条竖线间的点按照横分组,然后进行统计。这里用到map比较容易实现。
//不等,不问,不犹豫,不回头.
#include<bits/stdc++.h>
#define _ 0
#define ls p<<1
#define db double
#define rs p<<1|1
#define P 1000000007
#define ll long long
#define INF 1000000000
#define get(x) x=read()
#define PLI pair<ll,int>
#define PII pair<int,int>
#define ull unsigned long long
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define rep(x,y,z) for(int x=y;x<=z;++x)
#define fep(x,y,z) for(int x=y;x>=z;--x)
#define go(x) for(int i=link[x],y=a[i].y;i;y=a[i=a[i].next].y)
using namespace std;
const int N=1e6+10;
int n,m,k,heng[N],shu[N],vish[N],viss[N],b1[N],b2[N];
struct dian{int x,y;}a[N];
map<int,int>mp;
inline int read()
{
int x=0,ff=1;
char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();}
while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*ff;
}
inline bool cmp1(int x,int y) {return a[x].x<a[y].x;}
inline bool cmp2(int x,int y) {return a[x].y<a[y].y;}
int main()
{
//freopen("1.in","r",stdin);
int get(T);
while(T--)
{
get(n);get(m);get(k);
memset(vish,0,sizeof(vish));
memset(viss,0,sizeof(viss));
rep(i,1,n)
{
get(shu[i]);
viss[shu[i]]=1;
}
rep(i,1,m)
{
get(heng[i]);
vish[heng[i]]=1;
}
rep(i,1,k) get(a[i].x),get(a[i].y);
int n1=0,n2=0;
rep(i,1,k)
{
if(vish[a[i].y]&&viss[a[i].x]) continue;
if(vish[a[i].y]) b1[++n1]=i;
else b2[++n2]=i;
}
sort(b1+1,b1+n1+1,cmp1);
sort(b2+1,b2+n2+1,cmp2);
ll ans=0;
int j=1;
rep(i,1,n-1)//统计i和i+1两条竖线之间的点对。
{
int sm=0;
while(j<=n1&&a[b1[j]].x>shu[i]&&a[b1[j]].x<shu[i+1])
{
mp[a[b1[j]].y]++;
sm++;++j;
}
for(auto x:mp)
{
sm-=x.second;
ans+=(ll)x.second*sm;
}
mp.clear();
}
j=1;
rep(i,1,m-1)
{
int sm=0;
while(j<=n2&&a[b2[j]].y>heng[i]&&a[b2[j]].y<heng[i+1])
{
mp[a[b2[j]].x]++;
sm++;++j;
}
for(auto x:mp)
{
sm-=x.second;
ans+=(ll)x.second*sm;
}
mp.clear();
}
putl(ans);
}
return (0^_^0);
}
//以吾之血,铸吾最后的亡魂.
E. Playoff Restoration
关于这个题,感慨是读错题意了,导致怎么想都不对,首先队伍的排列只能是1,2,3,4,5...这样排列,不存在全排列种排列方法,那么剩下的问题就在于每场比赛的胜负问题了。考虑k<=4时,一共进行\(2^{k}-1\)场比赛,最多进行15场比赛我们直接枚举每场比赛的胜负即可。但对于k=5,我们只能进一步思考如何做。
想到比赛的结果是相互独立的,而且k=4可以,而k=5不行,都已经提示的这么明显了,我们可以进行折半搜索。也就是说我们先进行搜索前16个队伍的比赛情况,将所有能得到的h值记录下来。之后在搜索17-32队伍的比赛情况,之后再得到一个h值,然后根据给定的H看是否存在\(h_1+h_2=H\)的情况。即可。
//不等,不问,不犹豫,不回头.
#include<bits/stdc++.h>
#define _ 0
#define ls p<<1
#define db double
#define rs p<<1|1
#define P 998244353
#define ll long long
#define INF 1000000000
#define get(x) x=read()
#define PLI pair<ll,int>
#define PII pair<int,int>
#define ull unsigned long long
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define rep(x,y,z) for(int x=y;x<=z;++x)
#define fep(x,y,z) for(int x=y;x>=z;--x)
#define go(x) for(int i=link[x],y=a[i].y;i;y=a[i=a[i].next].y)
using namespace std;
const int N=100;
ll b[10][N],K,A,H,ars[3],c[N],ID;
ll zw[N];
bool flag=false;
map<ll,bool>mp[2];
inline int read()
{
int x=0,ff=1;
char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();}
while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*ff;
}
inline ll power(ll x,int y)
{
ll ans=1;
while(y)
{
if(y&1) ans=ans*x%P;
y>>=1;
x=x*x%P;
}
return ans%P;
}
inline void dfs(int n,ll d,int op)
{
if(n==0)
{
if(op==1)
{
ll ans=(d+b[n][1]*power(A,2)%P)%P;
mp[0][ans]=1;
ans=(d+b[n][1]*A%P)%P;
mp[1][ans]=1;
}
else
{
ll ans=(d+b[n][1]*power(A,2))%P;
ll s=(H-ans+P)%P;
if(mp[1].find(s)!=mp[1].end())
{
ars[1]=s;ars[2]=ans;ID=1;
flag=true;return;
}
ans=(d+b[n][1]*A)%P;
s=(H-ans+P)%P;
if(mp[0].find(s)!=mp[0].end())
{
ars[1]=s;ars[2]=ans;ID=2;
flag=true;return;
}
}
return;
}
rep(i,0,(1<<(1<<n-1))-1)//枚举所有的比赛情况
{
ll ans=d;
rep(j,0,(1<<n-1)-1)
{
int x=(j+1)*2-1;
if(i&1<<j)
{
b[n-1][j+1]=b[n][x];
ans=(ans+b[n][x+1]*power(A,(1<<n)+1)%P)%P;
}
else
{
b[n-1][j+1]=b[n][x+1];
ans=(ans+b[n][x]*power(A,(1<<n)+1)%P)%P;
}
}
dfs(n-1,ans,op);
if(flag) return;
}
}
inline void dfs1(int n,ll d,int op)
{
if(n==0)
{
if(ID==1)
{
if(op==1)
{
ll ans=(d+b[n][1]*A%P)%P;
if(ans==ars[op]) {c[b[n][1]]=1;flag=true;return;}
}
else
{
ll ans=(d+b[n][1]*power(A,2)%P)%P;
if(ans==ars[op]) {c[b[n][1]]=2;flag=true;return;}
}
}
else
{
if(op==1)
{
ll ans=(d+b[n][1]*power(A,2)%P)%P;
if(ans==ars[op]) {c[b[n][1]]=2;flag=true;return;}
}
else
{
ll ans=(d+b[n][1]*A%P)%P;
if(ans==ars[op]) {c[b[n][1]]=1;flag=true;return;}
}
}
return;
}
rep(i,0,(1<<(1<<n-1))-1)//枚举所有的比赛情况
{
ll ans=d;
rep(j,0,(1<<n-1)-1)
{
int x=(j+1)*2-1;
if(i&1<<j)
{
b[n-1][j+1]=b[n][x];
c[b[n][x+1]]=(1<<n)+1;
ans=(ans+b[n][x+1]*power(A,(1<<n)+1)%P)%P;
}
else
{
b[n-1][j+1]=b[n][x+1];
c[b[n][x]]=(1<<n)+1;
ans=(ans+b[n][x]*power(A,(1<<n)+1)%P)%P;
}
}
dfs1(n-1,ans,op);
if(flag) return;
}
}
int main()
{
//freopen("1.in","r",stdin);
get(K);get(A);get(H);
if(K==1)
{
if((A+A*A*2)%P==H) printf("%d %d\n",1,2);
else if((A*A+A*2)%P==H) printf("%d %d\n",2,1);
else puts("-1");
return 0;
}
rep(i,1,(1<<K-1)) b[K-1][i]=i;
dfs(K-1,0,1);//K-1为当前剩下的队伍的规模。
rep(i,1,(1<<K-1)) b[K-1][i]=i+(1<<K-1);
dfs(K-1,0,2);
if(!flag) {puts("-1");return 0;}
rep(i,1,(1<<K-1)) b[K-1][i]=i;
flag=false;dfs1(K-1,0,1);
rep(i,1,(1<<K-1)) b[K-1][i]=i+(1<<K-1);
flag=false;dfs1(K-1,0,2);
rep(i,1,1<<K) printf("%lld ",c[i]);
return (0^_^0);
}
//以吾之血,铸吾最后的亡魂.


