最小割模型
模型算不上,只能是入门的了,至于最小割=最大流的基础知识就不在多说了,这里以例题为主:
切糕
这不是一个随便建一下图就完了吗?....qwq(日常被大佬嘲讽的蒟蒻....)
这个题目的题意吧,多读几遍,画个图,再不行,先搁那,等几天再看他就会了...
反正是毒瘤的题意,反正你看题不要和实际生活联系起来就行了....大概题意就是对于每一个点对(x,y)(\(1\le x\le P,1\le y\le Q\))都找一个值\(f(x,y)\),满足\(1\le f(x,y) \le R\),且相邻距离为1的点对要满足\(\mid f(x,y)-f(x',y') \mid \le D\).而对于每一个形如\((x,y,f(x,y))的点对都有他的价值\),求如何为每一个点对安排一个\(f(x,y)\),使得在满足上面条件的情况下总价值最小?
对于这种毒瘤题吧,不能太快,慢慢来,不然真的会自闭的。
先看下数据范围,嗯\(P,Q,R\)最大是\(50\),铁定是网络流的题目了,之后呢咋建图???
算了,先考虑没有D的情况下,我们怎么做?没有D的话,每一个点对都是相对独立的,我们直接在每一个点对之间选取最小价值的\(f(x,y)\)即可,这显然是最优的.可是这和网络流有啥关系,这是这是....
这不就是最小割吗?我们将一个点拆成\(R\)个点,将他们串联起来,边得容量就是他们的价值,这找最小的过程不就是找到一条最小的边吗?
好了,起码我们现在将图建出来了,这个其实蛮好理解的,每个点对必须且只能选一个\(f\)值,这不就是最小割吗?选取最小的边使得S,T不连通.
之后考虑D的限制,我们观察题目给的条件,为啥有绝对值啊,太\(ugly\)了,不行,给他去掉,我们瞎画画图,发现其实就是对于相对距离为1的点对,必须满足\(f(x,y)-f(x',y')\le D\)且\(f(x,y)-f(x',y')\ge -D\)
我们将后面的式子变形一下,咦这不就是\(f(x',y')-f(x,y)\le D\)吗?怎么和第一个式子长得好一样,难道是双胞胎好了,这样我们只需要维护一个信息了,因为当我们枚举到\(f(x',y')\)的时候自然就会满足\(f(x,y)\)的要求了,这个咋维护呢?先来张图:
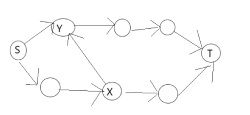
假若D=1,我们选了某个点对的x,对于与他相邻的点对必须选择y之后的点,只有这样才能满足要求,所以我们假想x之后的边割掉之后,怎样才能保证y后面的边也被割掉,我们可以从x向y连边,这样的话如果割掉y之前的边,还是联通的,所以就保证了y之后的边被割掉.既然到这了,这道题就没了.
//不等,不问,不犹豫,不回头.
#include<bits/stdc++.h>
#define _ 0
#define ls p<<1
#define db double
#define rs p<<1|1
#define RE register
#define ll long long
#define INF 1000000000
#define get(x) x=read()
#define PLI pair<ll,int>
#define PII pair<int,int>
#define pb(x) push_back(x)
#define ull unsigned long long
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define rep(x,y,z) for(RE int x=y;x<=z;++x)
#define fep(x,y,z) for(RE int x=y;x>=z;--x)
#define go(x) for(RE int i=link[x],y=a[i].y;i;y=a[i=a[i].next].y)
using namespace std;
const int N=42*40*40;
int P,Q,R,id[42][42][42],D;
int link[N],tot=1,s,t,d[N],current[N];
int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1};
struct edge{int y,next,v;}a[N*50];
char *fs,*ft,buf[1<<15];
inline char getc() {return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;}
inline int read()
{
int x=0,ff=1;
char ch=getc();
while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getc();}
while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getc();}
return x*ff;
}
inline void add(int x,int y,int v)
{
a[++tot].y=y;a[tot].v=v;a[tot].next=link[x];link[x]=tot;
a[++tot].y=x;a[tot].v=0;a[tot].next=link[y];link[y]=tot;
}
inline bool bfs()
{
queue<int>q;q.push(s);
memset(d,0,sizeof(d));
memcpy(current,link,sizeof(current));
d[s]=1;
while(!q.empty())
{
int x=q.front();q.pop();
go(x)
{
if(!a[i].v||d[y]) continue;
d[y]=d[x]+1;
q.push(y);
if(y==t) return true;
}
}
return false;
}
inline int dinic(int x,int flow)
{
if(x==t) return flow;
int rest=flow,k;
for(RE int i=current[x];i&&rest;i=a[i].next)
{
current[x]=i;
int y=a[i].y;
if(a[i].v&&d[y]==d[x]+1)
{
k=dinic(y,min(rest,a[i].v));
if(!k) d[y]=-1;
a[i].v-=k;
a[i^1].v+=k;
rest-=k;
}
}
return flow-rest;
}
int main()
{
//freopen("1.in","r",stdin);
get(P);get(Q);get(R);get(D);
s=0;t=P*Q*R+1;
int num=0;
rep(z,1,R) rep(x,1,P) rep(y,1,Q) id[x][y][z]=++num;
rep(z,1,R) rep(x,1,P) rep(y,1,Q)
{
int get(w);
if(z==1) add(s,id[x][y][z],INF);
if(z!=R) add(id[x][y][z],id[x][y][z+1],w);
else add(id[x][y][z],t,w);
if(z-D>=1)
{
rep(i,0,3)
{
int t1=x+dx[i],t2=y+dy[i];
if(t1>=1&&t1<=P&&t2>=1&&t2<=Q) add(id[x][y][z],id[t1][t2][z-D],INF);
}
}
}
int maxflow=0,flow;
while(bfs()) while(flow=dinic(s,INF)) maxflow+=flow;
put(maxflow);
return (0^_^0);
}
//以吾之血,铸吾最后的亡魂.
接下里这道题就比较毒瘤了....

这是数据范围:

偶买噶的,这才五十,网络流说:快块快,让我来....
这可真的算是一个真毒瘤题,记得曾经模拟考出过这个题,不过由于知识有限,就先咕掉了,没想到现在还能遇见他,真以为我是好惹的,一直来找我!
尽管怒火中烧,但还是得慢慢来,首先思考如果没有相交的限制条件的话,肯定是每个炮塔直接找他这一列/一行最大值,或许会有冲突那直接建图,每一个点向左右都连边,把流量当做边的容量,这样就能解决冲突了。
等等,冷静冷静冷静,这样的话跑出来的好像是最小的价值啊,跑出来的是最小割啊!
仔细思考下将炮塔所在的行/列连成一条链,在链尾连\(T\),这样跑出来的好像确实是最小的值,可我们想要的是最大值。怎么办?
这个时候就需要用一些骚操作,我们可以将所有的边权\(c\)魔改成\(INF-c\),这样我们跑出来的仍然是最小的,但观察下式子,\(INF-c\)最小,对应的\(c\)不就是最大的吗?好了,最优性确定了,不过由于是最小割的模型,就用最小割的思路来继续搞这个东西。
这样之后还发现一个问题,就是如果两条轨迹相交的话,我们发现两两的S和T是相互限制的.好像不能简单的搞出来...
那我们直接将这条链单独拎出来,也就是将多建几个交点,就行了。
之后就考虑如何考虑相交的事情我们发现用上一道题的方法就行了....细节贼多.....
//不等,不问,不犹豫,不回头.
#include<bits/stdc++.h>
#define _ 0
#define ls p<<1
#define db double
#define rs p<<1|1
#define RE register
#define P 999911659
#define ll long long
#define INF 1000000000
#define get(x) x=read()
#define PLI pair<ll,int>
#define PII pair<int,int>
#define pb(x) push_back(x)
#define ull unsigned long long
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define rep(x,y,z) for(RE int x=y;x<=z;++x)
#define fep(x,y,z) for(RE int x=y;x>=z;--x)
#define go(x) for(RE int i=link[x],y=a[i].y;i;y=a[i=a[i].next].y)
using namespace std;
const int N=52*52*4,maxn=2010;
int link[N],tot=1,n,m,c[N][N],pos[61][61],id,s,t,d[N],current[N];
struct edge{int y,next,v;}a[N<<6];
char *fs,*ft,buf[1<<15];
inline char getc() {return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;}
inline int read()
{
int x=0,ff=1;
char ch=getc();
while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getc();}
while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getc();}
return x*ff;
}
inline void add(int x,int y,int v)
{
a[++tot].y=y;a[tot].v=v;a[tot].next=link[x];link[x]=tot;
a[++tot].y=x;a[tot].v=0;a[tot].next=link[y];link[y]=tot;
}
inline bool bfs()
{
queue<int>q;q.push(s);
memset(d,0,sizeof(d));
memcpy(current,link,sizeof(current));
d[s]=1;
while(!q.empty())
{
int x=q.front();q.pop();
go(x)
{
if(!a[i].v||d[y]) continue;
d[y]=d[x]+1;
q.push(y);
if(y==t) return true;
}
}
return false;
}
inline int dinic(int x,int flow)
{
if(x==t) return flow;
int rest=flow,k;
for(RE int i=current[x];i&&rest;i=a[i].next)
{
current[x]=i;
int y=a[i].y;
if(a[i].v&&d[y]==d[x]+1)
{
k=dinic(y,min(rest,a[i].v));
if(!k) d[y]=-1;
a[i].v-=k;
a[i^1].v+=k;
rest-=k;
}
}
return flow-rest;
}
int main()
{
freopen("cti.in","r",stdin);
freopen("cti.out","w",stdout);
get(n);get(m);s=++id;t=++id;
int num=0;
rep(i,1,n) rep(j,1,m)
{
get(c[i][j]);
if(c[i][j]<0) ++num;
}
rep(i,1,n) rep(j,1,m)
{
if(c[i][j]==-3)
{
rep(k,1,j) pos[i][k]=++id;
add(s,pos[i][j],maxn);add(pos[i][1],t,maxn-c[i][1]);
fep(k,j,2) add(pos[i][k],pos[i][k-1],maxn-c[i][k]);
}
else if(c[i][j]==-4)
{
rep(k,j,m) pos[i][k]=++id;
add(s,pos[i][j],maxn);add(pos[i][m],t,maxn-c[i][m]);
rep(k,j,m-1) add(pos[i][k],pos[i][k+1],maxn-c[i][k]);
}
}
rep(i,1,n) rep(j,1,m)
{
if(c[i][j]==-1)
{
++id;add(s,id,maxn-c[1][j]);
int last=id;
rep(k,1,i-1)//连从i向i+1行的边..
{
++id;
add(last,id,maxn-c[k+1][j]);
if(pos[k][j]) add(pos[k][j],last,INF);
last=id;
}
add(id,t,maxn);
}
else if(c[i][j]==-2)
{
++id;add(s,id,maxn-c[n][j]);
int last=id;
fep(k,n,i+1)
{
++id;
add(last,id,maxn-c[k-1][j]);
if(pos[k][j]) add(pos[k][j],last,INF);
last=id;
}
add(id,t,maxn);
}
}
int maxflow=0,flow;
while(bfs()) while(flow=dinic(s,INF)) maxflow+=flow;
put(num*maxn-maxflow);
return (0^_^0);
}
//以吾之血,铸吾最后的亡魂.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号