斜率优化复习
真是的今天考了斜率优化的板子题,才知道自己关于斜率优化的知识早就已经枯竭了....从头理一下做题的思路吧!
这里就从一到例题着手吧!
任务安排
首先分析题意列出状态,设f[i]表示前\(i\)个任务都被安排过的最小话费。
转移式如下:f[i]=\(\sum_{j=0}^{i-1}\)min(f[j]\(+\)s\(\times\)(sumc[n]\(-\)sumc[j])\(+\)(sumc[i]\(-\)sumc[j])\(\times\)sumt[i])
考虑暴力的话就是,对于每一个i枚举一个j作为前驱,复杂度O(\(n^2\)).
优化的话就是今天讲的斜率优化了,先将式子拆开并将min函数去掉.如下:
f[i]\(=\)f[j]\(+\)s\(\times\)sumc[n]\(-\)s\(\times\)sumc[j]\(+\)sumt[i]\(\times\)sumc[i]\(-\)sumt[i]\(\times\)sumc[j]
由于i在最外层循环,我们将与\(i\)有关的量当成定值,所以这里的变量就只剩下f[j],sumc[j],我们移项,使得与j有关的分居等号两边且让j和i的乘积项作为斜率,具体的见下:
f[j]\(=\)(s+sumt[i]])\(\times\)sumc[j]+f[i]-s\(\times\)sumc[n]\(-\)sumt[i]\(\times\)sumc[i]
我们发现如果将sumc[j]和f[j]看做两个变量的话,则这是一个直线的表达式,自变量x是sumc[j],因变量y是f[j]。而这个决策j带来的f[i]则在截距中。如果我们将这些sumc[j]和f[j]放到一个坐标系中的话,对于每一个i来说他的所有候选决策,就是一堆点,而最大的f[i]就是对所有的点做一个特定斜率的直线,纵截距最大的j所带来的的f[i]值。
如下:

之后考虑如何有效的维护这个信息,这就要用到凸壳的知识了,发现如果对于最大的截距的话,仅有上凸壳上的点才有可能,对于最小截距的话,仅有下凸壳上的点才有可能。
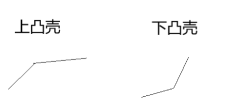
可以发现上凸壳上的直线的斜率是低的,而下凸壳的直线斜率为上升的,所以可以用单调队列来维护决策的之间斜率,从而维护这个凸壳。
对于这道题来说,随着i的增加,斜率s+sumt[i]也是单调递增的,我们不必维护整个凸壳,每次讲凸壳左部斜率小于s+sumt[i]的弹出去,这样每次从队头取出来的就是最优决策。复杂度O(n)
//不等,不问,不犹豫,不回头.
#include<bits/stdc++.h>
#define _ 0
#define ls p<<1
#define db double
#define rs p<<1|1
#define RE register
#define P 999911659
#define ll long long
#define INF 1000000000
#define get(x) x=read()
#define PLI pair<ll,int>
#define PII pair<int,int>
#define pb(x) push_back(x)
#define ull unsigned long long
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define rep(x,y,z) for(RE int x=y;x<=z;++x)
#define fep(x,y,z) for(RE int x=y;x>=z;--x)
#define go(x) for(RE int i=link[x],y=a[i].y;i;y=a[i=a[i].next].y)
using namespace std;
const int N=3e5+10;
ll sumc[N],sumt[N],n,s,q[N],l,r;
ll f[N];
inline int read()
{
int x=0,ff=1;
char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();}
while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*ff;
}
inline db X(int i) {return sumc[i];}
inline db Y(int i) {return f[i];}
inline db xie(int a,int b) {return (Y(b)-Y(a))/(X(b)-X(a));}
int main()
{
//freopen("1.in","r",stdin);
get(n);get(s);
rep(i,1,n)
{
int get(x1),get(x2);
sumt[i]=sumt[i-1]+x1;
sumc[i]=sumc[i-1]+x2;
}
rep(i,1,n)
{
db k=s+sumt[i];
while(l<r&&k>=xie(q[l],q[l+1])) ++l;
int j=q[l];
f[i]=f[j]+(ll)s*(sumc[n]-sumc[j])+(ll)(sumc[i]-sumc[j])*sumt[i];
while(l<r&&xie(q[r-1],q[r])>=xie(q[r],i)) --r;
q[++r]=i;
}
putl(f[n]);
return (0^_^0);
}
//以吾之血,铸吾最后的亡魂.
之后再来一个例题:
任务安排
这不是和上一个题一模一样吗?qwq....直接将上一个代码复制粘贴,欧耶,双倍经验!
等等怎么才65啊,不应该啊,我写个对拍,拍啊拍啊,拍了5万多组了,还是没有问题...
这就是某个蒟蒻干出来的事,再仔细看一下数据范围,咦,这里的\(T_i\)怎么多来个绝对值....再看一下上面的思路,看看对哪一步有影响...
由于\(T_i\)可以为负数(倒是很想知道啥任务需要时间为负数....),所以s\(+\)sumt[i]就没有单调性了,我们就不能讲凸壳的左部从单调队列中弹掉了,因为可能之后的i可能会用到,所以这里保留整个凸壳,之后选择决策时也不能单纯的选择最左部的点,应该二分一个点使得这个点之前的斜率小于k,之后的斜率大于等于k.总复杂度O(nlogn).
//不等,不问,不犹豫,不回头.
#include<bits/stdc++.h>
#define _ 0
#define ls p<<1
#define db double
#define rs p<<1|1
#define RE register
#define P 999911659
#define ll long long
#define INF 1000000000
#define get(x) x=read()
#define PLI pair<ll,int>
#define PII pair<int,int>
#define pb(x) push_back(x)
#define ull unsigned long long
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define rep(x,y,z) for(RE int x=y;x<=z;++x)
#define fep(x,y,z) for(RE int x=y;x>=z;--x)
#define go(x) for(RE int i=link[x],y=a[i].y;i;y=a[i=a[i].next].y)
using namespace std;
const int N=3e5+10;
ll sumc[N],sumt[N],n,s,q[N],l,r;
ll f[N];
inline int read()
{
int x=0,ff=1;
char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();}
while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*ff;
}
inline db X(int i) {return sumc[i];}
inline db Y(int i) {return f[i];}
inline db xie(int a,int b)
{
if(fabs(X(b)-X(a))<1e-8) return INF;
return (Y(b)-Y(a))/(X(b)-X(a));
}
inline int find(db k)
{
if(l==r) return q[l];
int L=l,R=r;
while(L<R)
{
int mid=L+R>>1;
if(xie(q[mid],q[mid+1])>=k) R=mid;
else L=mid+1;
}
return q[L];
}
int main()
{
//freopen("1.in","r",stdin);
get(n);get(s);
rep(i,1,n)
{
int get(x1),get(x2);
sumt[i]=sumt[i-1]+x1;
sumc[i]=sumc[i-1]+x2;
}
rep(i,1,n)
{
db k=s+sumt[i];
int j=find(k);
f[i]=f[j]+s*(sumc[n]-sumc[j])+(sumc[i]-sumc[j])*sumt[i];
while(l<r&&xie(q[r-1],q[r])>=xie(q[r],i)) --r;
q[++r]=i;
}
putl(f[n]);
return (0^_^0);
}
//以吾之血,铸吾最后的亡魂.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号