行列式与霍尔基夫矩阵
先打好基础,我们定义一个行列式
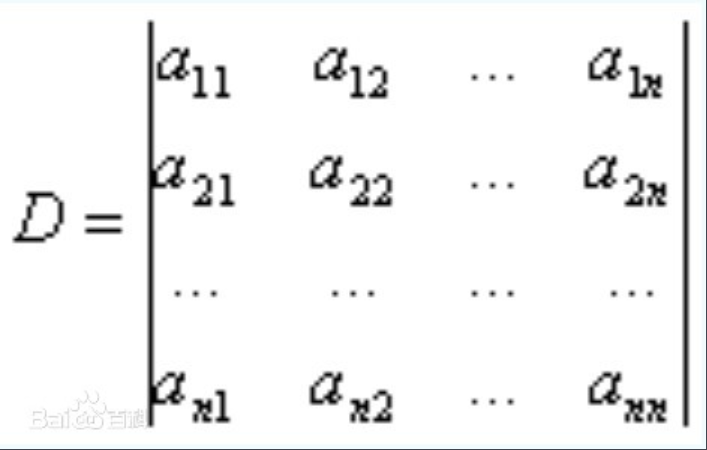
这样就是一个n阶行列式.
之后就是行列式的计算方法,先水一波二阶行列式的计算方法.
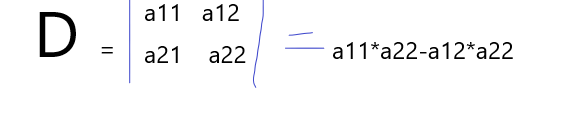
无脑记就行了.
余子式:就是去掉某一行某一列构成的行列式.
代数余子式,前面加个(-1)^(i+j)即可.
之后就是展开定理

k表示任一行.A表示代数余子式...
这里用几个例子(娱乐)来说明一下(表白专用):

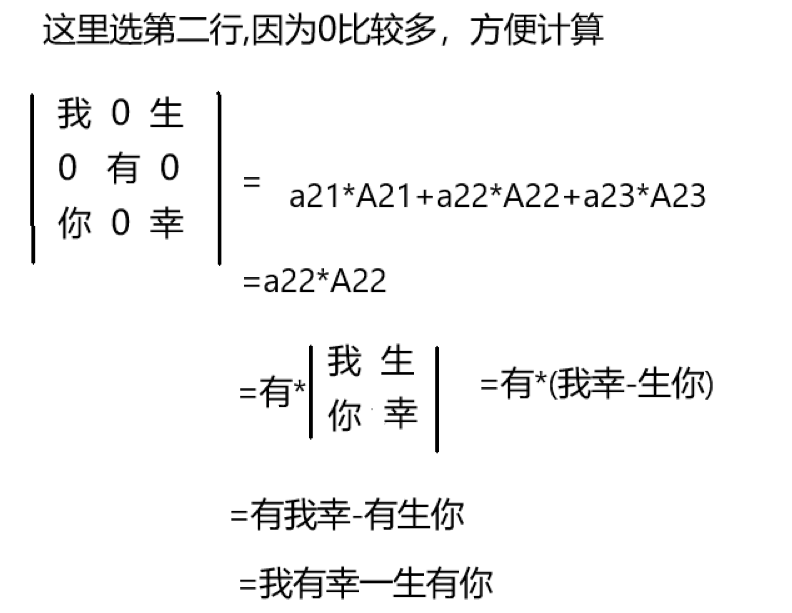
嗯,展开定理大概知道了,就来看看今天的主题吧:
http://www.lydsy.com/JudgeOnline/problem.php?id=1002
这个鬼畜的题,该开始用组合数学往死里推,到最后一交全wrong.....究其原因,没办法合理的统计不合法的方案数.毕竟还和容斥有关...
正解是用霍尔基夫矩阵解生成树的个数...
生成树计数一般都由霍尔基夫矩阵求解。求解相对广泛,一般均可求无向图的生成树的个数.
对于一个无向图我们定义它的霍尔基夫矩阵 ![]() 定义为: L=D-A
定义为: L=D-A
其中:D矩阵叫做【度矩阵】;A矩阵叫做【邻接矩阵】
这里定义就不详细解释了(D矩阵就是一个点的度数.注意只有i==j时才有值.A矩阵当u,v存在边时,才有值为1)
基尔霍夫矩阵矩阵树定理:基尔霍夫矩阵C的任意余子式Mij的行列式的值就是图G的生成树个数。
嗯,不要问为什么,记住就行....
之后我们的任务就是如何高出来一个行列式的值.
证明略....(原谅我的偷懒....证明太繁琐了...)
嗯递推式:f[n]=3*f[n-1]-f[n-2]+2.最后写上高精就行了..
强烈建议这个博客:好的博客


 浙公网安备 33010602011771号
浙公网安备 33010602011771号