splay入门

安利好的博客

好迷平衡树这一块....

今天先学一些其中splay的一些简单操作吧！

平衡树属于二叉查找树的一种,简单定义是：对于任意一个节点而言：左儿子内的节点都比他小,而右节点都比它大..

例如此树：

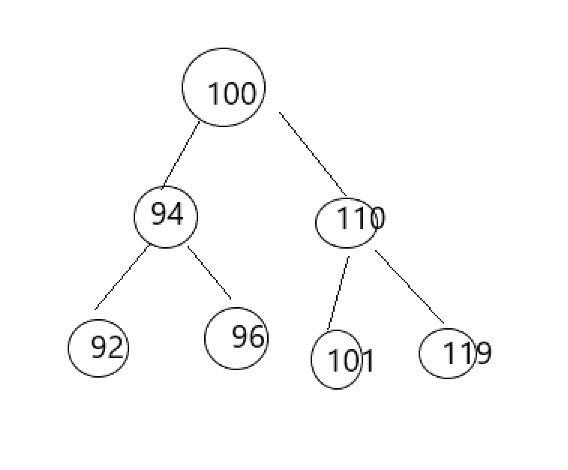
这就是一个二叉查找树...

至于splay有什么神奇的奇特之处,嗯就是旋转....我们如果要将一个点x将其与父亲y调换以下的话.就可以避免贝卡成链的情况..

共有四种情况：

    

   

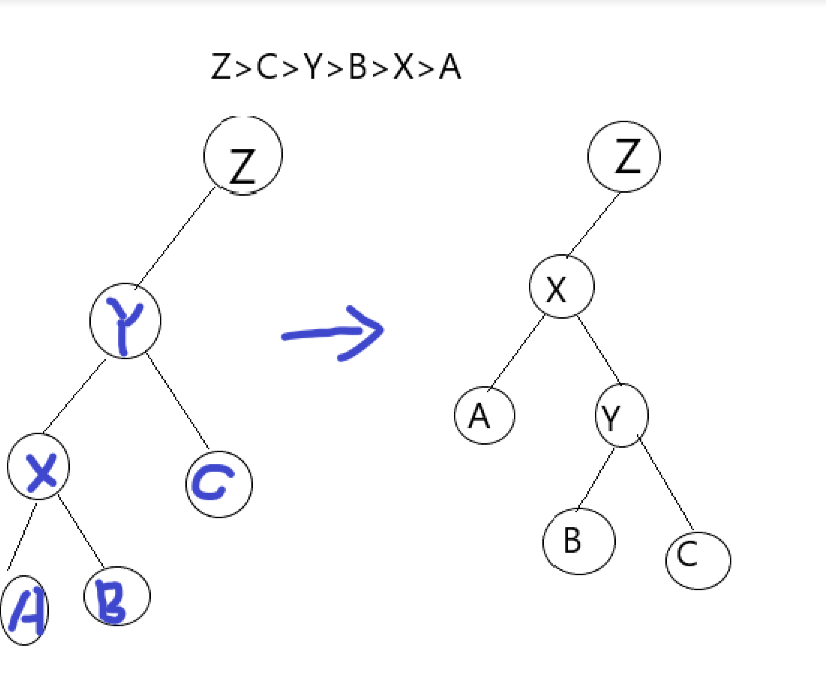
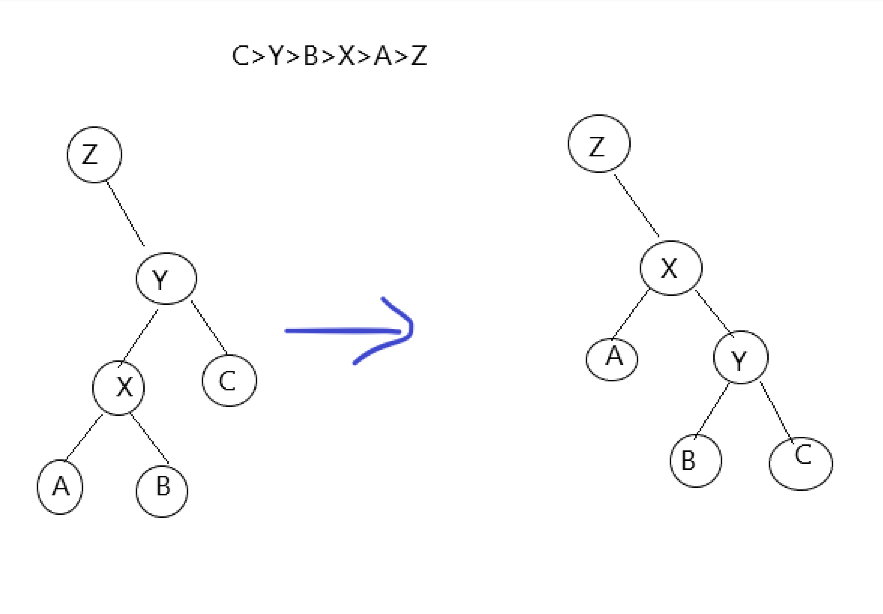
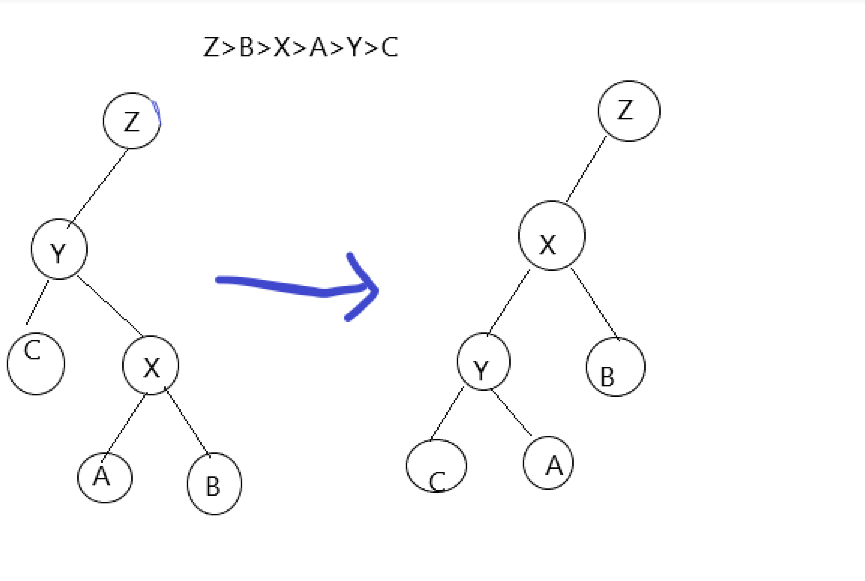
这是全部的四种情况,我们发现可以找规律：

1：x变为y在z中的位置.

2.y变为x在y中相反的位置.

3.x的 与x在y中位置 相同位置的儿子与x的位置关系不变.

4:x的 与x在y中位置 相反位置的儿子变成y中与原本在x中相同的位置的儿子.(真绕....)

5:y除x的3儿子与y的相对位置不变...

用代码就是这样的:

//其实旋转操作大体分三步：
//1.将x提上去.
//2.将x的与x在y中位置不相同的儿子给y.
//3.y到x的与x在y中位置不相同的儿子的位置. 
inline void retate(int x)
{
    int y=t[x].ff;//x的父亲 
    int z=t[y].ff;//y的父亲. 
    int k=t[y].ch[1]==x;//x是y的哪一个儿子.0是左儿子,y是右儿子.
    t[z].ch[t[c].ch[1]==y]=x;//从上往下更新.原本y的位置由x顶替. 
    t[x].ff=z;//x的父亲变成z
    t[y].ch[k]=t[x].ch[k^1];//先替换x中与x在y中位置相反的儿子.防止之后被覆盖.
    t[t[x].ch[k^1]].ff=y;//更新父亲节点. 
    t[x].ch[k^1]=y;//x的与x在y中位置相反的儿子变成y. 
    t[y].ff=x; //更新父亲节点. 
} 

多画图,多动手,你会恍然大悟的...

这就是基本操作了(大雾...)

接下来思考这样的问题:

如果我们要让x一直到某一个点的儿子怎么办,一直向上旋转吗？

例如下面东西：

 

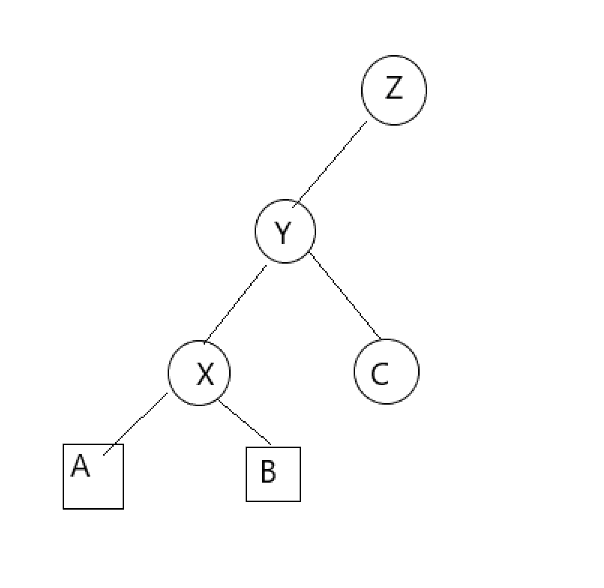
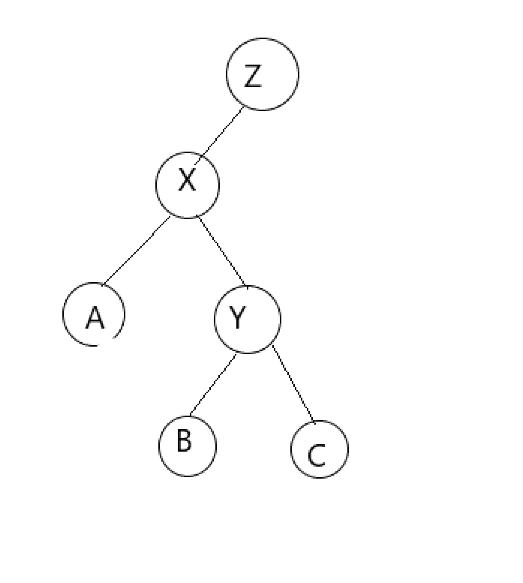
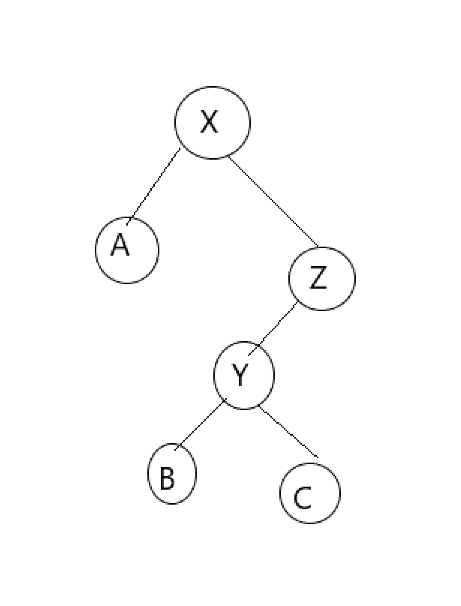
我们发现这样确实是可以的,但有一个弊端,不知道你们发现了没有？x旋转前与旋转后,始终有x,y,z,b这条链,那如果在这条链上查找的话复杂度就可能被卡成O(n^2)的.这我们不能接受.

其实再画画图就会发现，(我真的累了..),总共才两种情况...

1.x和y所属位置与y和z所属位置相同...

2.....不同

发现第一种情况与上面的样例相同,我们可以先旋转y,再旋转x,第二种情况直接旋转x即可.

inline void splay(int x,int goal)
{
    while(t[x].ff!=goal)//x一直旋转,直到是goal的儿子 
    {
        int y=t[x].ff,z=t[y].ff;//找到x的父亲,y的父亲. 
        if(y!=goal) (t[y].ch[0]==x)^(t[z].ch[0]==y):retato(y)?retato(x);//分类讨论 
        retato(x);//最后都旋转x 
    }
    if(goal==0) root=x;//更新根. 
}

好,到这里splay最核心的操作就完毕了,之后就是各个功能的应用.

首先是定义：

struct wy
{
    int val;//权值
    int ff;//父节点.
    int ch[2];//左右两个儿子.0是左儿子,1是右儿子.
    int cnt;//这个权值的节点出现的次数.
    int sum;//子节点的数量.  
}; 

 

插入操作：

当树为空时,直接新建一个节点即可.

树不空时,从根开始往下走.

inline int newpoint(int v,int fa)
{
    t[++tot].ff=fa; 
    t[tot].v=v;
    t[tot].sum=cnt=1;
    return tot;
} 
 
inline void insert(int x)
{
    int now=root;
    if(now==0) {root=newpoint(x,0);return;}//如果树为空. 
    while(1)
    {
        t[now].sum++; //依次更新子树个数. 
        if(t[now].val==x) {t[now].cnt++;splay(now,0);return;}//找到与x相同的值,累加一下数量. 
        int next=x>t[now].val;//找到下一个去的方向. 
        if(!t[now].ch[next])//如果找到最后没有相同的值,新建节点. 
        {
            int p=newpoint(x,now);
            t[now].ch[next]=p;
            splay(p,root);return;//维护形态. 
        }
        now=t[now].ch[next];//往下找. 
    }
}

查找数x的位置：

inline void find(int x)
{
    int now=root;
　　if(!now) return;
　　while(x!=v(now)&&t[now].ch[x>v(now)]) now=t[now].ch[x>v(now)];
　　splay(now,0);
} 

 

查找前驱/后继：

(这是在提前加入了INF和-INF的前提下)

inline int Next(int x,int op) //找前驱0/后继1
{
    find(x);
    int now=root;
    if(v(now)>x&&op) return now;//如果不存在x的话,find函数实质上返回了一个x的前驱或后继. 
    if(v(now)<x&&!op) return now;//所以这里就可以特判一些情况. 
    now=t[now].ch[op];//之后的情况就是存在x或find找的值与我们期望的值不对等. 
    while(t[now].ch[op^1]) now=t[now].ch[op^1];//(我们想要前驱,它找了后继,我们想要后继,它找了前驱.)
    return now;
}

 

删除操作：

删除权值为x的数：

inline void Delete(int x)
{
    int last=Next(x,0);//查找这个点的前驱 
    int next=Next(x,1);//查找这个点的后继 
    splay(last,0);splay(next,last);//将前驱搞到根.后继搞到前驱的右儿子. 
    int del=t[next].ch[0];//此时比前驱大且比后继大,只有x. 
    if(cnt(del)>=2) 
    {
        cnt(del)--;//数量大于2,减少一 
        splay(del,0);
    }
    else t[next].ch[0]=0;//否则直接搞掉. 
}

 

查找第k大;

inline int kth(int x) 
{
    int now=root;//当前根节点. 
    if(sum[x]<x) return 0;//不存在. 
    while(1)
    {
        int y=t[now].ch[0];//左儿子. 
        if(x>sum(y)+cnt(now))//左儿子里无排名第k大. 
        {
            x-=sum(y)+cnt(now);//更新排名. 
            now=t[now].ch[1];//到右儿子上 
        }
        else if(sum(y)>=x) now=y;//到左儿子 
        else return v(now);//放回这个节点. 
    }
}