树状数组
个人觉得树状数组十分好用,虽然功能十分简单,但却可以用来优化其他题中的查询与修改...
数据结构就没学多少,就学好这个吧!
单点修改与区间查询:
#include<bits/stdc++.h> using namespace std; const int N=501000; int n,m,a[N],c[N]; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} return x*ff; } inline int lowbit(int x) {return x&(-x);} inline void add(int x,int k) { for(;x<=n;x+=lowbit(x)) c[x]+=k; } inline int ask(int x) { int ans=0; for(;x>0;x-=lowbit(x)) ans+=c[x]; return ans; } int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(register int i=1;i<=n;++i) a[i]=read(),add(i,a[i]); for(register int i=1;i<=m;++i) { int p=read(),x=read(),y=read(); if(p==1) add(x,y); else if(p==2) printf("%d\n",ask(y)-ask(x-1)); } return 0; }
区间修改与单点查询:

#include<bits/stdc++.h> using namespace std; const int N=501000; int n,m,a[N],c[N]; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} return x*ff; } inline int lowbit(int x){return x&(-x);} inline void add(int x,int k) { for(;x<=n;x+=lowbit(x)) c[x]+=k; } inline int ask(int x) { int ans=0; for(;x>0;x-=lowbit(x)) ans+=c[x]; return ans; } int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(register int i=1;i<=n;++i) a[i]=read(),add(i,a[i]-a[i-1]); for(register int i=1;i<=m;++i) { int p=read(); if(p==1) { int x=read(),y=read(),k=read(); add(x,k);add(y+1,-k); } else if(p==2) { int x=read(); printf("%d\n",ask(x)); } } return 0; }

#include<bits/stdc++.h> #define ll long long using namespace std; const ll N=101000; ll n,m,sum1[N],sum2[N],a[N]; inline ll read() { ll x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} return x*ff; } inline ll lowbit(ll x){return x&(-x);} inline void add(ll x,ll k) { int i=x; for(;x<=n;x+=lowbit(x)) sum1[x]+=k,sum2[x]+=(i-1)*k; } inline ll ask(ll x) { ll ans=0,i=x; for(;x>0;x-=lowbit(x)) ans+=i*sum1[x]-sum2[x]; return ans; } int main() { freopen("1.in","r",stdin); n=read();m=read(); for(register int i=1;i<=n;++i) a[i]=read(),add(i,a[i]-a[i-1]); for(register int i=1;i<=m;++i) { int p=read(); if(p==1) { ll x=read(),y=read(),k=read(); add(x,k);add(y+1,-k); } else if(p==2) { ll x=read(),y=read(); printf("%ld\n",ask(y)-ask(x-1)); } } return 0; }
好,这样就全齐了,总结一下,其中单点修改,单点查询,区间查询就是比较传统的树状数组..而区间修改则需要更改为差分,区间查询则更需要多开一个数组...
例题:
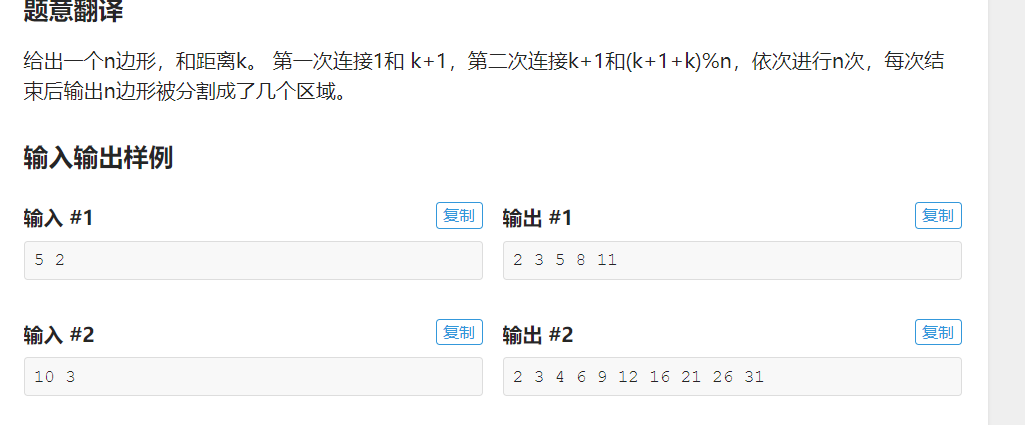
#include<bits/stdc++.h> #define ll long long using namespace std; ll n,k,c[1001000],s,ans=1; inline ll read() { ll x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} return x*ff; } inline ll lowbit(ll x) {return x&(-x);} inline void add(ll x,ll k) { for(;x<=n;x+=lowbit(x)) c[x]+=k; } inline ll ask(ll x) { ll ans=0; for(;x>0;x-=lowbit(x)) ans+=c[x]; return ans; } int main() { //freopen("1.in","r",stdin); n=read();k=read();s=1; for(register ll i=1;i<=n;++i) { ll x=(k*i+1)%n; if(!x) x=n; if(x<s) { if((s-x)<(n-s+x)) ans+=ask(s-1)-ask(x); else ans+=2*(i-1)-ask(s)+ask(x-1); } else if(x>s) { if((x-s)<(n-x+s)) ans+=ask(x-1)-ask(s); else ans+=2*(i-1)-ask(x)+ask(s-1); } add(x,1);add(s,1);s=x;ans++; printf("%ld ",ans); } return 0; }
二维:
单点修改与区间查询.
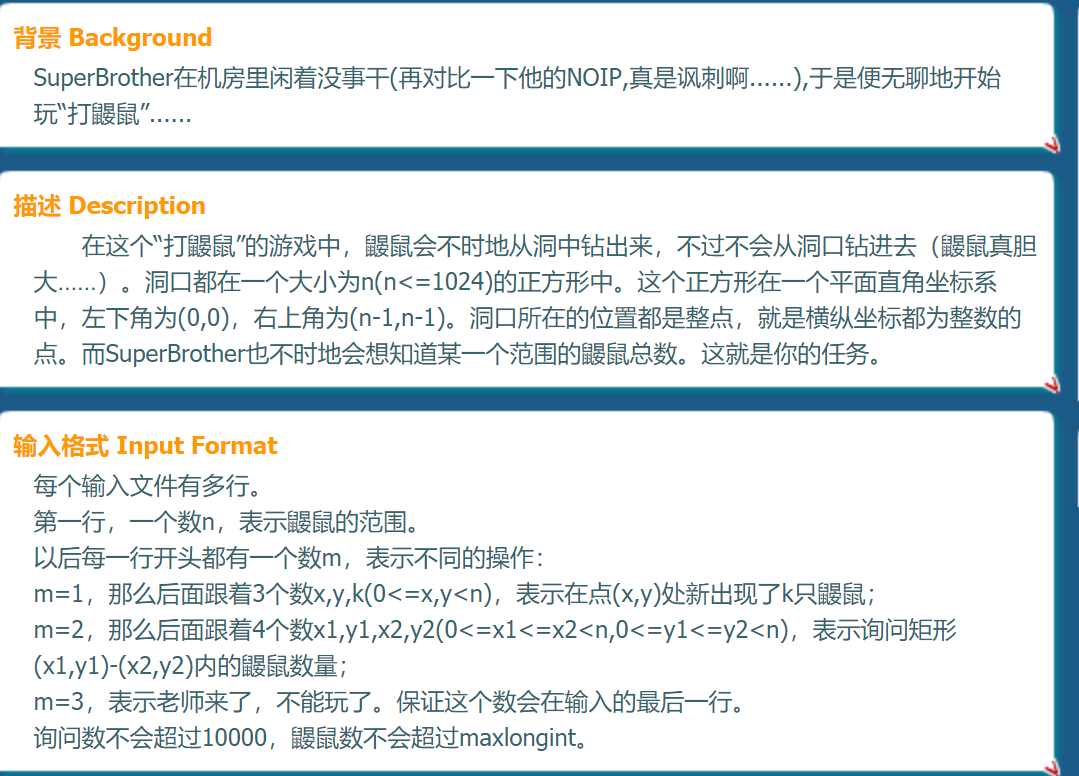
这里注意0的lowbit就行...
#include<bits/stdc++.h> #define ll long long using namespace std; const int N=1100; ll c[N][N],n,m,a[N][N]; inline ll read() { ll x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) {if(ch=='-') ff=-1;ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} return x*ff; } inline ll lowbit(ll x) {return x&(-x);} inline void add(ll x,ll y,ll k) { ll yy=y; for(;x<=n;x+=lowbit(x)) for(y=yy;y<=n;y+=lowbit(y)) c[x][y]+=k; } inline ll ask(ll x,ll y) { ll yy=y,ans=0; for(;x>0;x-=lowbit(x)) for(y=yy;y>0;y-=lowbit(y)) ans+=c[x][y]; return ans; } int main() { freopen("1.in","r",stdin); n=read()+1; for(;;) { int p=read(); if(p==3) break; else if(p==1) { ll x=read()+1,y=read()+1,k=read(); add(x,y,k); } else if(p==2) { ll x1=read()+1,y1=read()+1,x2=read()+1,y2=read()+1; printf("%lld\n",ask(x2,y2)-ask(x1-1,y2)-ask(x2,y1-1)+ask(x1-1,y1-1)); } } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号