拓扑排序总结
不说了,上题:
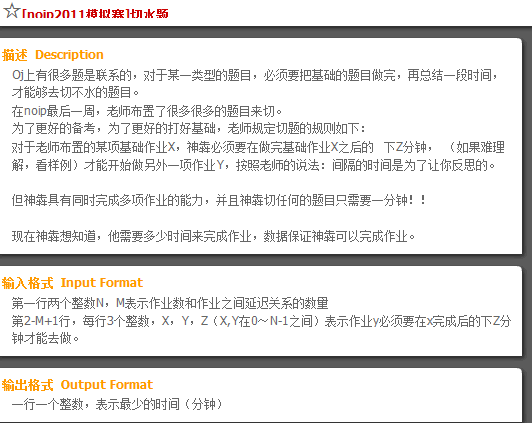
这个题其实很简单,显而易见X就是Y的先决条件,Z就是边权了,注意细节就行,最后将出度为0的点取个max即为答案。
代码如下:

#include<bits/stdc++.h> using namespace std; int n,m,tot,link[10000],ru[500],chu[500],z[500],o,s[500]; struct bian { int y,next,v; }; bian a[10000]; queue<int>q; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') ff=-1; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*ff; } inline void add(int x,int y,int v) { a[++tot].y=y; a[tot].v=v; a[tot].next=link[x]; link[x]=tot; } inline void work1() { while(q.size()) { int x=q.front();q.pop(); for(int i=link[x];i;i=a[i].next) { int y=a[i].y; s[y]=s[x]+a[i].v;ru[y]--; if(ru[y]==0) q.push(y); } } int maxx=-1213214324; for(int i=1;i<=o;i++) { if(s[z[i]]>maxx) maxx=s[z[i]]; } cout<<maxx<<endl; } int main() { freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=m;i++) { int x=read(),y=read(),v=read(); add(x,y,v); chu[x]++;ru[y]++; } for(int i=0;i<n;i++) { if(ru[i]==0) {s[i]=1;q.push(i);} if(chu[i]==0) z[++o]=i; } work1(); return 0; }
下一题:
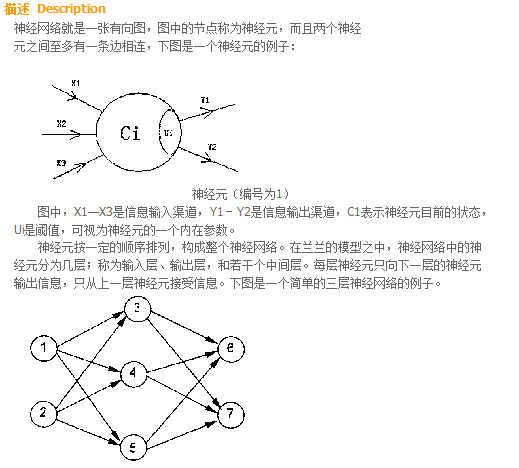

这个题其实也是类似前面的是后面的入度,因为想要知道后面点的C值必须知道他前面的入度边的权值与C值,这就构成了强制的依赖关系,即后面的点依赖前面的点,剩下的就是细节问题了,注意判别是否为兴奋即可。
代码:

#include<bits/stdc++.h> using namespace std; int tot,c[500],link[500],u[500],n,p,ru[500],chu[500],z[500],o; struct bian { int y,v,next; }; bian a[10000]; queue<int>q; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') ff=-1; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*ff; } inline void add(int x,int y,int v) { a[++tot].y=y; a[tot].v=v; a[tot].next=link[x]; link[x]=tot; } inline void work1() { while(q.size()) { int x=q.front();q.pop(); for(int i=link[x];i;i=a[i].next) { int y=a[i].y; c[y]=c[y]+a[i].v*c[x]; ru[y]--; if(ru[y]==0) { c[y]=c[y]-u[y]; if(c[y]>0) q.push(y); } } } int pd=0; for(int i=1;i<=o;i++) { if(c[z[i]]>0) { pd=1; cout<<z[i]<<' '<<c[z[i]]<<endl; } } if(pd==0) cout<<"NULL"<<endl; } int main() { freopen("1.in","r",stdin); n=read();p=read(); for(int i=1;i<=n;i++) { c[i]=read();u[i]=read(); } for(int i=1;i<=p;i++) { int x=read(),y=read(),v=read(); add(x,y,v);chu[x]++;ru[y]++; } for(int i=1;i<=n;i++) { if(ru[i]==0) q.push(i); if(chu[i]==0) z[++o]=i; } work1(); return 0; }
最后一题:
 这个
这个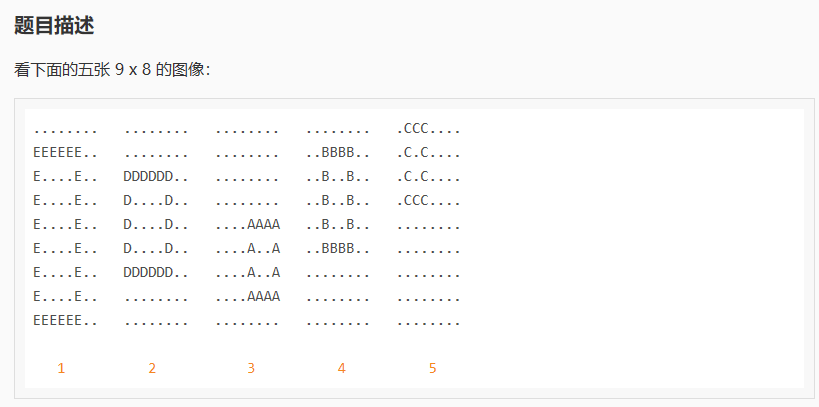
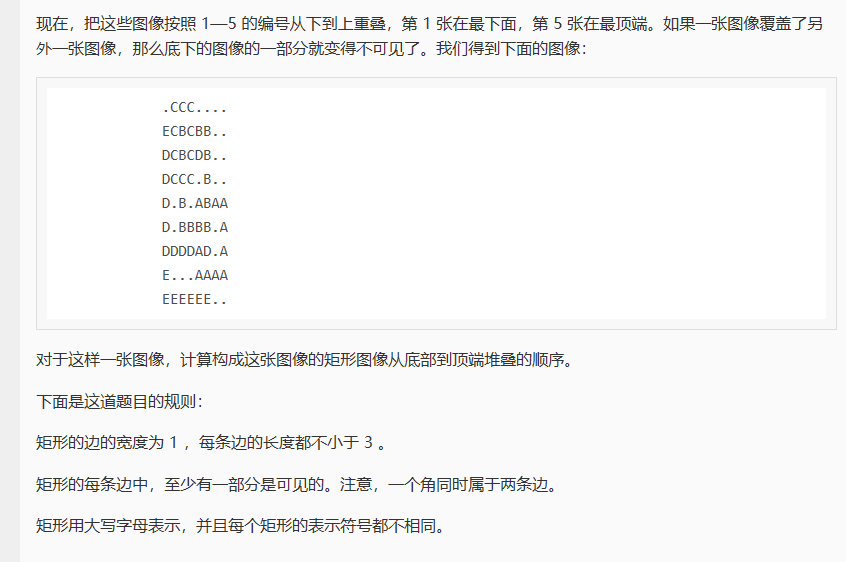
这个题猛的一看和图没关系呀!于是就理所当然的去打了个爆搜dfs,暴力寻找当前的每一个完整矩阵,然后去掉,继续寻找,当然加上回溯,因为要加上所有的结果...
暴力的算法非常好想,但代码就...反正鄙人是折腾了一天才调出来了暴力的代码...
以下就是了,有心情的看一眼:

#include<bits/stdc++.h> using namespace std; int a[100][100],h,w,n,f[100],o; string s[100],s1; struct zuo { int x1,y1,x2,y2; }; zuo z[30]; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') ff=-1; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*ff; } inline int shu(char a) { return (int(a-'A'+1)); } bool check(int s) { for(int i=z[s].x1;i<=z[s].x2;i++) { if(a[i][z[s].y1]!=s&&a[i][z[s].y1]!=0) return false; if(a[i][z[s].y2]!=s&&a[i][z[s].y2]!=0) return false; } for(int i=z[s].y1;i<=z[s].y2;i++) { if(a[z[s].x1][i]!=s&&a[z[s].x1][i]!=0) return false; if(a[z[s].x2][i]!=s&&a[z[s].x2][i]!=0) return false; } return true; } void xiao(int s) { for(int i=z[s].x1;i<=z[s].x2;i++) a[i][z[s].y1]=a[i][z[s].y2]=0; for(int i=z[s].y1;i<=z[s].y2;i++) a[z[s].x1][i]=a[z[s].x2][i]=0; } inline void dfs(int p,string r) { if(p==n) { s[++o]=r;return; } for(int i=1;i<=26;i++) { if(check(i)&&f[i]==1) { f[i]=0; int l[100][100]; memcpy(l,a,sizeof(l)); xiao(i); dfs(p+1,char(i+'A'-1)+r); memcpy(a,l,sizeof(a)); f[i]=1; } } } int main() { freopen("1.in","r",stdin); h=read();w=read(); for(int i=1;i<=26;i++) { z[i].x1=z[i].y1=8475834; z[i].x2=z[i].y2=0; } for(int i=1;i<=h;i++) { for(int j=1;j<=w;j++) { char ch; cin>>ch; if(ch=='.') a[i][j]=-1; else { int x=shu(ch); if(f[x]==0) { f[x]=1;n++; } a[i][j]=x; z[x].x1=min(z[x].x1,i); z[x].y1=min(z[x].y1,j); z[x].x2=max(z[x].x2,i); z[x].y2=max(z[x].y2,j); } } } dfs(0,s1); sort(s+1,s+1+o); for(int i=1;i<=o;i++) cout<<s[i]<<endl; return 0; }
正解当然就是今天讲的拓扑了,或许有人就会问了,这个题连图都没有,怎么就和拓扑有关系了?
大家都知道上面这张图会遮盖下面这张图,所以对于下面的这张图来说他会有所缺失,那些不属于它的其他字母就是它上面的图留下的,那要搜索这张图的矩阵,就必须把它上面这张图的矩阵去掉,这样就构成了强制的依赖关系,也就是说一张图的矩阵要想完整必须把不属于他的矩阵字母去掉,这样就不难看出这张图中不属于他的字母就是它的入度,这样就可以建图了,当然为了找出所有的结果,还需要用到dfs,不过用的是拓扑的做法。
代码如下:

#include<bits/stdc++.h> using namespace std; int h,w,link[100000],tot,n,f[100],b[100][100],ru[30],o,ff[30]; string s[100000],s0; struct bian { int y,next; }; bian a[100000]; struct zuo { int x1,y1,x2,y2; }; zuo z[100]; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') ff=-1; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*ff; } inline int shu(char a) { return (int(a-'A'+1)); } inline void add(int x,int y) { a[++tot].y=y; a[tot].next=link[x]; link[x]=tot; } inline void dfs(int p,string r) { if(p==n) {s[++o]=r;return;} for(int i=1;i<=26;i++) { if(f[i]==1&&ru[i]==0) { f[i]=0; for(int j=link[i];j;j=a[j].next) { int y=a[j].y;ru[y]--; } dfs(p+1,char(i+'A'-1)+r); f[i]=1; for(int j=link[i];j;j=a[j].next) { int y=a[j].y;ru[y]++; } } } } int main() { freopen("1.in","r",stdin); h=read();w=read(); for(int i=1;i<=26;i++) { z[i].x1=z[i].y1=23234232332; z[i].x2=z[i].y2=0; } for(int i=1;i<=h;i++) { for(int j=1;j<=w;j++) { char c; cin>>c; if(c=='.'){b[i][j]=-1;continue;} int x=shu(c);b[i][j]=x; if(f[x]==0){f[x]=1;n++;} z[x].x1=min(z[x].x1,i); z[x].y1=min(z[x].y1,j); z[x].x2=max(z[x].x2,i); z[x].y2=max(z[x].y2,j); } } for(int i=1;i<=26;i++) { if(f[i]==1) { memset(ff,0,sizeof(ff)); for(int j=z[i].x1;j<=z[i].x2;j++) { if(b[j][z[i].y1]!=i&&ff[b[j][z[i].y1]]==0) { ff[b[j][z[i].y1]]=1; add(b[j][z[i].y1],i);ru[i]++; } if(b[j][z[i].y2]!=i&&ff[b[j][z[i].y2]]==0) { ff[b[j][z[i].y2]]=1; add(b[j][z[i].y2],i);ru[i]++; } } for(int j=z[i].y1;j<=z[i].y2;j++) { if(b[z[i].x1][j]!=i&&ff[b[z[i].x1][j]]==0) { ff[b[z[i].x1][j]]=1; add(b[z[i].x1][j],i);ru[i]++; } if(b[z[i].x2][j]!=i&&ff[b[z[i].x2][j]]==0) { ff[b[z[i].x2][j]]=1; add(b[z[i].x2][j],i);ru[i]++; } } } } dfs(0,s0); sort(s+1,s+1+o); for(int i=1;i<=o;i++) cout<<s[i]<<endl; return 0; }
由此看出拓扑不仅可以解决图上的问题,还可以解决其他的问题,重点是找到其存在的强制的依赖关系,当你做题看到有这种关系存在时,不管是图不是,考虑一下拓扑,或许会有意外的收获!
最后还有一道拓扑的拓展

看到这一题,可能大家就有疑惑这和拓扑有什么关系?但其实由于数据太大,一个bfs并不能跑完。
我们看题得知:无环。我们就可以用c[i]数组保存从起点到i点的所有路径和,用f[i]保存从起点到i点的所有方法数,这时就有强制的依赖关系出现,要等到点x的入度为0时才能算出其c[x]的值与f[x]的值
以下是代码:

#include<bits/stdc++.h> using namespace std; int n,a[1000][1000],maxx,b[10000],qi=1,tot,pd,c[10000]; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') ff=-1; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*ff; } void dfs(int x) { for(int i=1;i<=maxx;i++) { if(a[x][i]) { a[x][i]--;a[i][x]--; dfs(i);c[++tot]=i; } } } int main() { freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { int x=read(),y=read(); a[x][y]++;a[y][x]++; maxx=max(maxx,x);maxx=max(maxx,y); b[x]++;b[y]++; } for(int i=1;i<=maxx;i++) { if(b[i]%2==1) { qi=i;break; } } dfs(qi);c[++tot]=qi; for(int i=tot;i>=1;i--) cout<<c[i]<<endl; return 0; }
好了,拓扑就讲到这,你学会了吗?



 浙公网安备 33010602011771号
浙公网安备 33010602011771号