小知识

1：memcpy的用法（y，x，n）；

y指的是要复制的目的地，也就是因变量。

x指的是要复制的本体，也就是自变量。

n指的是要复制的数量。

一般用是要新建一个新的数组当做中间的桥梁。

int l[100][100];
memcpy(l,a,sizeof(l));
dfs(p+1,char(i+'A'-1)+r);
memcpy(a,l,sizeof(a));

一般也是在dfs回溯时用，可以舍去那些冗杂的操作，且可以提高时间。

2：

  模运算的运算规则：   

注意模运算时要注意负余数的出现！！！

必须掌握：

  (a + b)  mod  p = (a  mod  p + b  mod  p)  mod  p            （1）
      (a - b)  mod  p = (a  mod  p - b  mod  p)  mod  p              （2） 
      (a * b)  mod  p = (a  mod  p * b  mod  p)  mod  p              （3）
      a^b  mod  p = ((a  mod  p)^b)  mod  p                              （4）

了解：
      结合率： ((a+b)  mod  p + c)  mod  p = (a + (b+c)  mod  p)  mod  p （5）
                     ((a*b)  mod  p * c) mod  p = (a * (b*c)  mod  p)  mod  p     （6）
      交换率： (a + b)  mod  p = (b+a)  mod  p                 （7）
                     (a * b)  mod  p = (b * a)  mod  p                 （8）
      分配率： ((a +b) mod  p * c)  mod  p = ((a * c)  mod  p + (b * c)  mod  p)  mod  p （9）
      重要定理：若a≡b ( mod  p)，则对于任意的c，都有(a + c) ≡ (b + c) ( mod p)；（10）
                        若a≡b ( mod  p)，则对于任意的c，都有(a * c) ≡ (b * c) ( mod p)；（11）
                        若a≡b ( mod  p)，则对于任意的c，都有ac≡ bc ( mod p)；     （13）

3：

int极大值：INT_MAX；

int极小值：INT_MIN；

4:

控制小数点的开关（cin）：

cin<<fixed<<setprecision(要保留的位数)<<要输出的double类型的数<<endl;

5：

优化max：#define max（a，b） (((a)>(b))?(a):(b))

优化min：#define min (a,b) (((a)<(b))?(a):(b))

6:

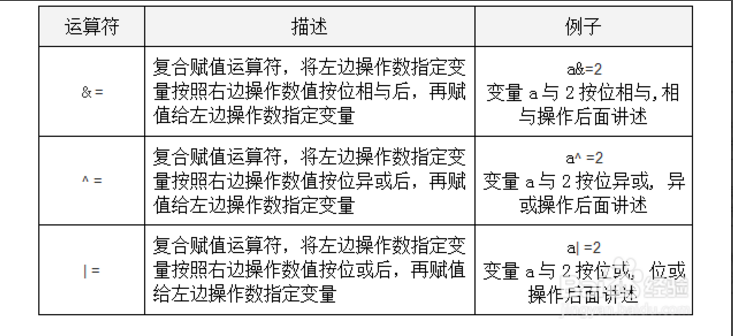
一:与运算：都为1取1，否则取0(有0取0，认0)；

二：异或运算：相同取0，不同取1；

可用于滚动数组的滚动，例

int u;
f[u][][]=;
for(int i=1;i<=n;i++)
{
    u=u^1;
    for(int j=1;j<=n;j++)
    {
        f[u][j]=min(f[u^1][j],f[u^1][j-w[i]]+r[i]);
    }
}

用u表示当前状态，u^1表示上一个状态；

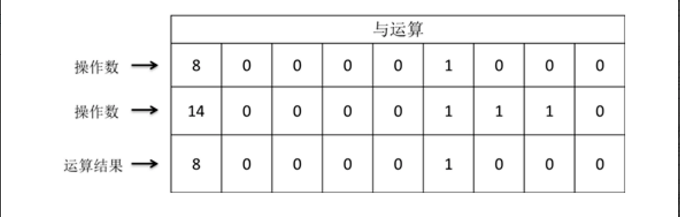
三：或运算：有1取1，否则为0（有1取1，认1）；

可用于bool类型状态的转移，因为未知状态都是0，若已知状态为1，则赋为1，否则为0；

例：

f[i][j][k]|=f[i-1][j-a[i]][k];

7：

快速幂：

求a的n次方，记住是要把n分成二进制的数：

ll kuaisu(ll x,ll y)
{
    ll ans=1;
    while(y)
    {
        if(y&1) ans=(ans*x)%mod;
        y>>=1;
        x=(x*x)%mod;
    }
    return ans;
}

记住把格式固定下来..

8：

计算时注意不要把long long 溢出，最好避免用乘法，用除法。

未完待续...