[WebGL入门]五,矩阵的基础知识
注:文章译自http://wgld.org/,原作者杉本雅広(doxas),文章中假设有我的额外说明。我会加上[lufy:],另外。鄙人webgl研究还不够深入,一些专业词语,假设翻译有误,欢迎大家指正。
不是让你到店前面排队
lufy:你一定奇怪。为什么叫这个题目,由于日语中的矩阵叫做“行列”,所以作者就给读者们开了个玩笑。我就这么直接翻译了,大家知道什么意思即可了。
在3D渲染的世界里,会非常频繁的用到矩阵。
这里所说的矩阵,是数学里的矩阵。英语中叫做Matrix。
矩阵尽管听起来好像非常easy,矩阵也有非常多种,并且计算方法非常难或者说非常麻烦。简单的说,矩阵就是把数字像箱子一样排列。将数字横竖排列起来就形成了矩阵。
在寻常的生活中是用不到的,可是在3D渲染的世界中却是必不可少的一个元素。
为什么须要矩阵
尽管说矩阵在3D渲染中必不可少,可是可能全然没有接触过它的人也不在少数。那为什么矩阵如此重要呢?
模拟三维空间。须要非常多的计算。什么样的东西,在哪里。什么角度。大小怎样,仅仅绘制想要绘制的模型数等等。都须要进行非常复杂且大量的计算。
矩阵就是像刚才说的那样,把数字依照行和列排列起来,在实际应用中。一个矩阵中能够包括非常多的情报。
比方说,想要绘制的模型在世界的什么位置放置着,是否发生了旋转,是否进行了放大和缩小,摄影的镜头在什么位置,镜头的方向怎样。终于成像后的画面的横竖比例怎样......等等,这些情报都能够用一个矩阵来表示。
假设你看了前面的文章(三。3D画图的基础知识)。并且你是个细心的人的话,应该注意到了吧,模型在世界的什么位置。镜头的方向等。前面都已经介绍过了。
也就是说,模型坐标变换,视图坐标变换,投影坐标变换。这些一连串的坐标变换假设使用矩阵的话,就能够在一个矩阵中完毕全部的坐标变换处理。
无论怎么说。为什么矩阵这么重要。大家应该大概了解了吧。
主要是,矩阵的计算效率非常高,并且及其便利。
3D渲染和矩阵
上面说矩阵是由数字组合起来的。那么矩阵究竟是个什么东西呢?
矩阵尽管有非常多种。当中的一种叫做方阵。就是行数和列数同样的矩阵。
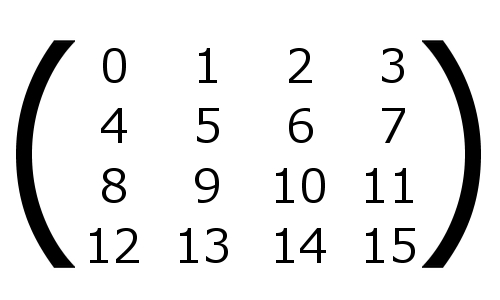
上面这种矩阵,就叫做方阵。
这种方阵,一般的3D渲染的世界中使用的是4x4的矩阵。就像刚刚给的图一样,行和列都是4个元素组成,这就是3D渲染中使用的矩阵的类型。
那为什么不是3x3的方阵或者其它的矩阵。而偏偏是4x4的方阵。这是有原因的。只是,如今先不用在意这些。仅仅要先记住。矩阵是能够让3D渲染中的计算变的简单的一个机制即可了。
矩阵全然是数学的话题,所以理解起来可能非常的难。
尽管说,最好是细致的学一下,可是如今的阶段。仅仅须要知道矩阵是个什么东西就能够了。*实际上。我也不是数学专业,也不可能对矩阵的每个细节都全然理解。
实际3D渲染的时候。像上面说的那样,准备好模型坐标变换。视图坐标变换。投影坐标变换的各个矩阵。再具体一点,就是准备好各种坐标变换的矩阵。然后相乘。将终于得到的矩阵传给WebGL的顶点着色器。
顶点着色器从传过来的矩阵中,获取到模型的坐标,加工到画面上显示出来。也就是说,操作坐标变换的矩阵,就能够决定模型在画面上怎样绘制。
矩阵能做什么
前面也说了,坐标变换有模型变换,视图变换,投影变换等多种。
矩阵能够将上面提到的变换保存起来,比方,假设是模型变换的矩阵。想要绘制的3D模型的位置,扩大缩小。以及旋转等信息。都能够定义在一个矩阵中。
视图变换矩阵,镜头的位置,镜头的方向。以及镜头对准了哪个点(注视点)等能够定义在一个矩阵中。投影变换矩阵的话。显示的横竖比例和视角等信息能够定义在一个矩阵中。
并且。这三个矩阵能够相互组合,终于得出的变换矩阵传给着色器,可是这里须要注意一点,假设是普通的数学计算,相乘的时候,不须要注意相乘的顺序,比方2x3等于6,3x2也等于6。可是矩阵的话。依据相乘的顺序得出的结果是不同的。由于矩阵的这种性质,所以进行模型。视图,投影的矩阵相乘的时候。要特别注意相乘的顺序。
到实际敲代码的时候,我会进一步具体说明,首先要记住矩阵相乘的顺序非常的重要。
总结
好了。说了这么多。对矩阵也多少有些了解了吧。
这次,不是让你全然理解矩阵,就是先介绍一下,假设要真的解说矩阵的话,你必须一个脚踩进数学世界的大门才行。
进行3D渲染,矩阵是必不可少的,并且要彻底理解矩阵是非常难的。所以如今先明确一下矩阵究竟是个什么东西即可了。
以后。我有可能会专门进行矩阵的解说,首先。简单理解一下就好。重要的是,比起零基础。先来知道一下矩阵的用处。假设有兴趣的话,网上有非常多相关的介绍,理解的越深肯定越好。
假设有时间的话,能够先自己看一下。
下一次。介绍一下3D中的术语顶点和多边形。


