遗传算法来控制进入一
博主前言:此文章来自一份网络资料,原作者不明,是我看过的最好的一份遗传算法教程,假设你能耐心看完他,相信你一定能基本掌握遗传算法。
遗传算法的有趣应用非常多,诸如寻路问题,8数码问题,囚犯困境,动作控制,找圆心问题(这是一个国外网友的建议:在一个不规则的多边形 中,寻找一个包括在该多边形内的最大圆圈的圆心。),TSP问题(在以后的章节里面将做具体介绍。),生产调度问题,人工生命模拟等。直到最后看到一个非 常有趣的比喻,认为由此引出的袋鼠跳问题(暂且这么叫它吧),既有趣直观又直达遗传算法的本质,确实非常适合作为刚開始学习的人入门的样例。
问题的提出与解决方式
让我们先来考虑考虑以下这个问题的解决的方法。
已知一元函数:
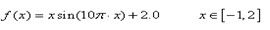
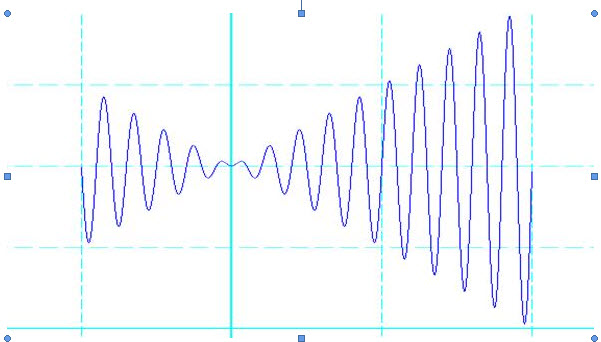
如今要求在既定的区间内找出函数的最大值
极大值、最大值、局部最优解、全局最优解
在解决上面提出的问题之前我们有必要先澄清几个以后将经常会碰到的概念:极 大值、最大值、局部最优解、全局最优解。学过高中数学的人都知道极大值在一个小邻域里面左边的函数值递增,右边的函数值递减,在图2.1里面的表现就是一 个“山峰”。当然,在图上有非常多个“山峰”,所以这个函数有非常多个极大值。而对于一个函数来说,最大值就是在全部极大值其中,最大的那个。所以极大值具有局部性,而最大值则具有全局性。
由于遗传算法中每一条染色体,相应着遗传算法的一个 解决方式,一般我们用适应性函数(fitness function)来衡量这个解决方式的优劣。所以从一个基因组到其解的适应度形成一个映射。所以也能够把遗传算法的过程看作是一个在多元函数里面求最优解的过程。在这个多维曲面里面也有数不清的“山峰”,而这些最优解所相应的就是局部最优解。而当中也会有一个“山峰”的海拔最高的,那么这个就是全局最优 解。而遗传算法的任务就是尽量爬到最高峰,而不是陷落在一些小山峰。(另外,值得注意的是遗传算法不一定要找“最高的山峰”,假设问题的适应度评价越小越好的话,那么全局最优解就是函数的最小值,相应的,遗传算法所要找的就是“最深的谷底”)假设至今你还不太理解的话,那么你先往下看。本章的演示样例程序将会 很形象的表现出这个情景。
“袋鼠跳”问题
既然我们把 函数曲线理解成一个一个山峰和山谷组成的山脉。那么我们能够设想所得到的每个解就是一仅仅袋鼠,我们希望它们不断的向着更高处跳去,直到跳到最高的山峰(虽然袋鼠本身不见得愿意那么做)。所以求最大值的过程就转化成一个“袋鼠跳”的过程。以下介绍介绍“袋鼠跳”的几种方式。
爬山法、模拟退火和遗传算法
解决寻找最大值问题的几种常见的算法:
1. 爬山法(最速上升爬山法):
从搜索空间中随机产生邻近的点,从中选择相应解最优的个体,替换原来的个体,不断 反复上述过程。由于仅仅对“邻近”的点作比較,所以目光比較“短浅”,经常仅仅能收敛到离开初始位置比較近的局部最优解上面。对于存在许多局部最长处的问题,通过一个简单的迭代找出全局最优解的机会很渺茫。(在爬山法中,袋鼠最有希望到达最靠近它出发点的山顶,但不能保证该山顶是珠穆朗玛峰,或者是一个很 高的山峰。由于一路上它仅仅顾上坡,没有下坡。)
2. 模拟退火:
这种方法来自金属热加工过程的启示。在金属热加工过程中,当金属的温度超过它的熔点(Melting Point)时,原子就会激烈地随机运动。与全部的其他的物理系统相类似,原子的这样的运动趋向于寻找其能量的极小状态。在这个能量的变迁过程中,開始时。温度非常高, 使得原子具有非常高的能量。随着温度不断减少,金属逐渐冷却,金属中的原子的能量就越来越小,最后达到全部可能的最低点。利用模拟退火的时候,让算法从较大的跳跃開始,使到它有足够的“能量”逃离可能“路过”的局部最优解而不至于限制在当中,当它停在全局最优解附近的时候,逐渐的减小跳跃量,以便使其“落脚 ”到全局最优解上。(在模拟退火中,袋鼠喝醉了,并且随机地大跳跃了非常长时间。运气好的话,它从一个山峰跳过山谷,到了另外一个更高的山峰上。但最后,它渐渐清醒了并朝着它所在的峰顶跳去。)
3. 遗传算法:
模拟物竞天择的生物进化过程,通过维护一个潜在解的群体运行了多方向的搜索,并支持这些方向上的信息构成和交换。以面为单位的搜索,比以点为单位的搜索,更能发现全局最优解。(在遗传算法中,有非常多袋鼠,它们降落到喜玛拉雅山脉的随意地方。这些袋鼠并不知道它们的任务是寻找珠穆朗玛峰。但每过几年,就在一些海拔高度较低的地方射杀一些袋鼠,并希望存活下来的袋鼠是多产的,在它们所处的地方生儿育女。)(后来,一个叫天行健的网游给我想了一个更恰切的故事:从前,有一大群袋鼠,它们被莫名其妙的零散地遗弃于喜马拉雅山脉。于是仅仅好在那里艰苦的生活。海拔 低的地方弥漫着一种无色无味的毒气,海拔越高毒气越稀薄。但是可怜的袋鼠们对此完全不觉,还是习惯于活蹦乱跳。于是,不断有袋鼠死于海拔较低的地方,而越是在海拔高的袋鼠越是能活得更久,也越有机会生儿育女。就这样经过很多年,这些袋鼠们居然都不自觉地聚拢到了一个个的山峰上,但是在全部的袋鼠中,仅仅有聚 拢到珠穆朗玛峰的袋鼠被带回了漂亮的澳洲。)
以下主要介绍介绍遗传算法实现的过程。
遗传算法的实现过程
遗传算法的实现过程实际上就像自然界的进化过程那样。首先寻找一种对问题潜在解进行“数字化”编码的方案。(建立表现型和基因型的映射关系。)然后用随机 数初始化一个种群(那么第一批袋鼠就被任意地分散在山脉上。),种群里面的个体就是这些数字化的编码。接下来,通过适当的解码过程之后,(得到袋鼠的位置 坐标。)用适应性函数对每个基因个体作一次适应度评估。(袋鼠爬得越高,越是受我们的喜爱,所以适应度对应越高。)用选择函数依照某种规定择优选 择。(我们要每隔一段时间,在山上射杀一些所在海拔较低的袋鼠,以保证袋鼠整体数目持平。)让个体基因交叉变异。(让袋鼠随机地跳一跳)然后产生子 代。(希望存活下来的袋鼠是多产的,并在那里生儿育女。)遗传算法并不保证你能获得问题的最优解,可是使用遗传算法的最大长处在于你不必去了解和担心怎样 去“找”最优解。(你不必去指导袋鼠向那边跳,跳多远。)而仅仅要简单的“否定”一些表现不好的个体即可了。(把那些总是爱走下坡路的袋鼠射杀。)以后你会 慢慢理解这句话,这是遗传算法的精粹!
所以我们总结出遗传算法的一般步骤:
開始循环直至找到惬意的解。
1.评估每条染色体所相应个体的适应度。
2.遵照适应度越高,选择概率越大的原则,从种群中选择两个个体作为父方和母方。
3.抽取父母两方的染色体,进行交叉,产生子代。
4.对子代的染色体进行变异。
5.反复2,3,4步骤,直到新种群的产生。
结束循环。
接下来,我们将具体地剖析遗传算法过程的每个细节。
编制袋鼠的染色体----基因的编码方式
通过前一章的学习,读者已经了解到人类染色体的编码符号集,由4种碱基的两种配合组成。共同拥有4种情况,相当于2 bit的信息量。这是人类基因的编码方式,那么我们使用遗传算法的时候编码又该怎样处理呢?
受到人类染色体结构的启示,我们能够设想一下,如果眼下仅仅有“0”,“1”两种碱基,我们也用一条链条把他们有序的串连在一起,由于每个单位都能表现出 1 bit的信息量,所以一条足够长的染色体就能为我们勾勒出一个个体的全部特征。这就是二进制编码法,染色体大致例如以下:
010010011011011110111110
上面的编码方式尽管简单直观,但明显地,当个体特征比較复杂的时候,须要大量的编码才干精确地描写叙述,对应的解码过程(类似于生物学中的DNA翻译过程,就是把基因型映射到表现型的过程。)将过份繁复,为改善遗传算法的计算复杂性、提高运算效率,提出了浮点数编码。染色体大致例如以下:
1.2 – 3.3 – 2.0 –5.4 – 2.7 – 4.3
那么我们怎样利用这两种编码方式来为袋鼠的染色体编码呢?由于编码的目的是建立表现型到基因型的映射关系,而表现型一般就被理解为个体的特征。比方人的基因型是46条染色体所描写叙述的(总长度 两 米的纸条?),却能解码成一个个眼,耳,口,鼻等特征各不同样的活生生的人。所以我们要想为“袋鼠”的染色体编码,我们必须先来考虑“袋鼠”的“个体特征”是什么。或许有的人会说,袋鼠的特征非常多,比方性别,身长,体重,或许它喜欢吃什么也能算作当中一个特征。但详细在解决问题的情况下,我们应该进 一步思考:不管这仅仅袋鼠是长短,肥瘦,仅仅要它在低海拔就会被射杀,同一时候也没有规定身长的袋鼠能跳得远一些,身短的袋鼠跳得近一些。当然它爱吃什么就更不相关了。我们由始至终都仅仅关心一件事情:袋鼠在哪里。由于仅仅要我们知道袋鼠在那里,我们就能做两件必须去做的事情:
(1)通过查阅喜玛拉雅山脉的地图来得知袋鼠所在的海拔高度(通过自变量求函数值。)以推断我们有不是必需把它射杀。
(2)知道袋鼠跳一跳后去到哪个新位置。
如 果我们一时无法准确的推断哪些“个体特征”是必要的,哪些是非必要的,我们经常能够用到这样一种思维方式:比方你觉得袋鼠的爱吃什么东西很必要,那么你就想一想,有两仅仅袋鼠,它们其他的个体特征全然同等的情况下,一仅仅爱吃草,另外一仅仅爱吃果。你会立即发现,这不会对它们的命运有丝毫的影响,它们应该有同 等的概率被射杀!仅仅因它们处于同一个地方。(值得一提的是,假设你的基因编码设计中包括了袋鼠爱吃什么的信息,这事实上不会影响到袋鼠的进化的过程,而那仅仅攀到珠穆朗玛峰的袋鼠吃什么也全然是随机的,可是它所在的位置却是很确定的。)
以上是对遗传算法编码过程中常常经历的思维过程,必须把详细问题抽象成数学模型,突出主要矛盾,舍弃次要矛盾。仅仅有这样才干简洁而有效的解决这个问题。希望刚開始学习的人细致琢磨。
既然确定了袋鼠的位置作为个体特征,详细来说位置就 是横坐标。那么接下来,我们就要建立表现型到基因型的映射关系。就是说怎样用编码来表现出袋鼠所在的横坐标。因为横坐标是一个实数,所以说透了我们就是要对这个实数编码。回想我们上面所介绍的两种编码方式,读者最先想到的应该就是,对于二进制编码方式来说,编码会比較复杂,而对于浮点数编码方式来说,则会 比較简洁。恩,正如你所想的,用浮点数编码,只须要一个浮点数而已。而以下则介绍怎样建立二进制编码到一个实数的映射。
明显地,一定长度的二进制编码序列,仅仅能表示一定精度的浮点数。譬如我们要求解精确到六位小数,由于区间长度为2 – (-1) = 3 ,为了保证精度要求,至少把区间[-1,2]分为3 × 106等份。又由于
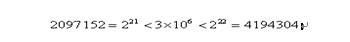
所以编码的二进制串至少须要22位。
把一个二进制串(b0,b1,....bn)转化位区间里面相应的实数值通过以下两个步骤。
(1)将一个二进制串代表的二进制数转化为10进制数:
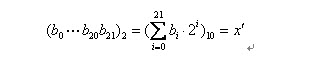
(2)相应区间内的实数:
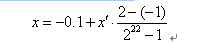
比如一个二进制串<1000101110110101000111>表示实数值0.637197。
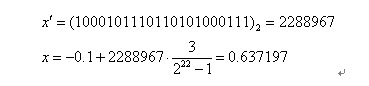
二进制串<0000000000000000000000>和<1111111111111111111111>则分别表示区间的两个端点值-1和2。
因为往下章节的演示样例程序差点儿都仅仅用到浮点数编码,所以这个“袋鼠跳”问题的解决方式也是採用浮点数编码的。往下的程序演示样例(包含装载基因的类,突变函数)都是针对浮点数编码的。(对于二进制编码这里仅仅作简单的介绍,只是这个“袋鼠跳”全然能够用二进制编码来解决的,并且更有效一些。所以读者能够自己尝试用 二进制编码来解决。)
我们定义一个类作为袋鼠基因的载体。(细心的人会提 出这种疑问:为什么我用浮点数的容器来储藏袋鼠的基因呢?袋鼠的基因不是仅仅用一个浮点数来表示即可吗?恩,没错,其实对于这个实例,我们仅仅须要用上一个浮点数即可了。我们这里用上容器是为了方便以后利用这些代码处理那些编码须要一串浮点数的问题。)
class Genome
{
public:
friend class GenAlg;
friend class GenEngine;
Genome():fitness(0){}
Genome(vector <double> vec, double f): vecGenome(vec), fitness(f){} //类的带參数初始化參数。
private:
vector <double> vecGenome; // 装载基因的容器
double fitness; //适应度
};
好了,眼下为止我们把袋鼠的染色体给研究透了,让我们继续跟进袋鼠的进化旅程。
物竞天择--适应性评分与及选择函数。
1.物竞――适应度函数(fitness function)
自然界生物竞争过程往往包括两个方面:生物相互间的搏斗与及生物与客观环境的搏斗过程。但在我们这个实例里面,你能够想象到,袋鼠相互之间是很友好的,它们并不须要互相搏斗以争取生存的权利。它们的生死存亡很多其它是取决于你的推断。由于你要衡量哪仅仅袋鼠该杀,哪仅仅袋鼠不该杀,所以你必须制定一个衡量的标准。而对于这个问题,这个衡量的标准比較easy制定:袋鼠所在的海拔高度。(由于你单纯地希望袋鼠爬得越高越好。)所以我们直接用袋鼠的海拔高度作为它们的适应性评分。即适应度函数直接返回函数值即可了。
2.天择――选择函数(selection)
自然界中,越适应的个体就越有可能生殖后代。可是也不能说适应度越高的就肯定后代越多,仅仅能是从概率上来说很多其它。(毕竟有些所处海拔高度较低的袋鼠非常幸运,逃过了你的眼睛。)那么我们怎么来建立这样的概率关系呢?以下我们介绍一种经常使用的选择方法――轮盘赌(Roulette Wheel Selection)选择法。如果种群数目,某个个体其适应度为,则其被选中的概率为:
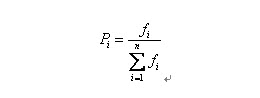
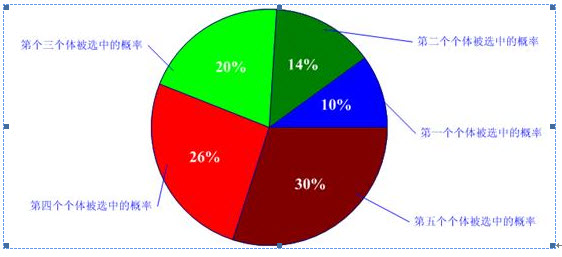
比方我们有5条染色体,他们所相应的适应度评分分别为:5,7,10,13,15。
所以累计总适应度为:
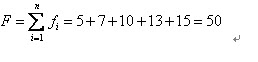
所以各个个体被选中的概率分别为:
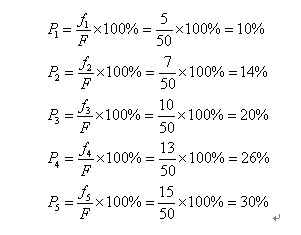
呵呵,有人会问为什么我们把它叫成轮盘赌选择法啊?事实上你仅仅要看看图2-2的轮盘就会明确了。这个轮盘是依照各个个体的适应度比例进行分块的。你能够想象一下,我们转动轮盘,轮盘停下来的时候,指针会随机地指向某一个个体所代表的区域,那么非常幸运地,这个个体被选中了。(非常明显,适应度评分越高的个体被选中的概率越大。)
那么接下来我们看看怎样用代码去实现轮盘赌。
Genome GenAlg:: GetChromoRoulette()
{
//产生一个0到人口总适应性评分总和之间的随机数.
//中m_dTotalFitness记录了整个种群的适应性分数总和)
double Slice = (random()) * totalFitness;
//这个基因将承载转盘所选出来的那个个体.
Genome TheChosenOne;
//累计适应性分数的和.
double FitnessSoFar = 0;
//遍历总人口里面的每一条染色体。
for (int i=0; i<popSize; ++i)
{
//累计适应性分数.
FitnessSoFar += vecPop[i].fitness;
//假设累计分数大于随机数,就选择此时的基因.
if (FitnessSoFar >= Slice)
{
TheChosenOne = vecPop[i];
break;
}
}
//返回转盘选出来的个体基因
return TheChosenOne;
}遗传变异――基因重组(交叉)与基因突变。
应该说这两个步骤就是使到子代不同于父代的根本原因(注意,我没有说是子代优于父代的原因,仅仅有经过自然的选择后,才会出现子代优于父代的倾向。)。对于这两种遗传操作,二进制编码和浮点型编码在处理上有非常大的差异,当中二进制编码的遗传操作过程,比較类似于自然界里面的过程,以下将分开讲述。
1.基因重组/交叉(recombination/crossover)
(1)二进制编码
回想上一章介绍的基因交叉过程:同源染色体联会的过程中,非姐妹染色单体(分别来自父母两方)之间经常发生交叉,而且相互交换一部分染色体,如图2-3。其实,二进制编码的基因交换过程也很类似这个过程――随机把当中几个位于同一位置的编码进行交换,产生新的个体,如图2-4所看到的。
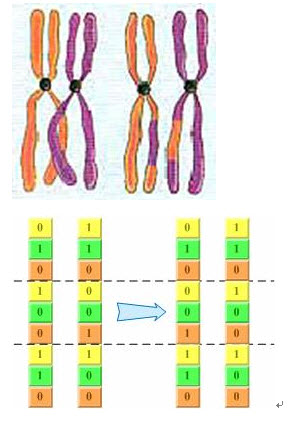
(2)浮点数编码
假设一条基因中含有 多个浮点数编码,那么也能够用跟上面类似的方法进行基因交叉,不同的是进行交叉的基本单位不是二进制码,而是浮点数。而假设对于单个浮点数的基因交叉,就有其他不同的重组方式了,比方中间重组:
这样仅仅要随机产生就能得到介于父代基因编码值和母代基因编码值之间的值作为子代基因编码的值。
考 虑到“袋鼠跳”问题的详细情况――袋鼠的个体特征只表现为它所处的位置。能够想象,同一个位置的袋鼠的基因是全然同样的,而两条同样的基因进行交叉后,相当于什么都没有做,所以我们不打算在这个样例里面使用交叉这一个遗传操作步骤。(当然硬要这个操作步骤也不是不行的,你能够把两只异地的袋鼠捉到一起, 让它们交配,然后产生子代,再把它们送到它们应该到的地方。)
2.基因突变(Mutation)
(1)二进制编码
相同回想一下上一章所介绍的基因突变过程:基因突变是染色体的某一个位点上基因的改变。基因突变使一个基因变成它的等位基因,而且一般会引起一定的表现型变化。恩,正如上面所说,二进制编码的遗传操作过程和生物学中的过程很相类似,基因串上的“ 0”或“ 1”有一定几率变成与之相反的“ 1”或“ 0”。比如以下这串二进制编码:
101101001011001
经过基因突变后,可能变成下面这串新的编码:
001101011011001
(2)浮点型编码
浮点型编码的基因突变过程通常是对原来的浮点数添加或者降低一个小随机数。比方原来的浮点数串例如以下:
1.2,3.4, 5.1, 6.0, 4.5
变异后,可能得到例如以下的浮点数串:
1.3,3.1, 4.9, 6.3, 4.4
当 然,这个小随机数也有大小之分,我们一般管它叫“步长”。(想想“袋鼠跳”问题,袋鼠跳的长短就是这个步长。)一般来说步长越大,開始时进化的速度会比較快,可是后来比較难收敛到精确的点上。而小步长却能较精确的收敛到一个点上。所以非常多时候为了加快遗传算法的进化速度,而又能保证后期可以比較精确地收敛 到最优解上面,会採取动态改变步长的方法。事实上这个过程与前面介绍的模拟退火过程比較相类似,读者可以做简单的回想。
以下是针对浮点型编码的基因突变函数的写法:
void GenAlg::Mutate(vector<double> &chromo)
{
//遵循预定的突变概率,对基因进行突变
for (int i=0; i<chromo.size(); ++i)
{
//假设发生突变的话
if (random() < mutationRate)
{
//使该权值添加或者降低一个非常小的随机数值
chromo[i] += ((random()-0.5) * maxPerturbation);
//保证袋鼠不至于跳出自然保护区.
if(chromo[i] < leftPoint)
{
chromo[i] = rightPoint;
}
else if(chromo[i] > rightPoint)
{
chromo[i] = leftPoint;
}
//以上代码非基因变异的一般性代码仅仅是用来保证基因编码的可行性。
}
}
}值得一提的是遗传算法中基因突变的特点和上一章提到的生物学中的基因突变的特点很相类似,这里回想一下:
1.基因突变是随机发生的,且突变频率非常低。(只是某些应用中须要高概率的变异)
2.大多数基因变异对生物本身是有害的。
3.基因突变是不定向的。
好了,到此为止,基因编码,基因适应度评估,基因选择,基因变异都一一实现了,剩下来的就是把这些遗传过程的“零件”装配起来了。
未完待续,承接下篇遗传算法入门到掌握(二)



