稀疏矩阵

一、稀疏矩阵的定义

　　对于那些零元素数目远远多于非零元素数目，而且非零元素的分布没有规律的矩阵称为稀疏矩阵（sparse）。
　　人们无法给出稀疏矩阵的确切定义，一般都仅仅是凭个人的直觉来理解这个概念，即矩阵中非零元素的个数远远小于矩阵元素的总数，而且非零元素没有分布规律。
　　　　

二、稀疏矩阵的压缩存储

　　因为稀疏矩阵中非零元素较少，零元素较多，因此能够採用仅仅存储非零元素的方法来进行压缩存储。
　　因为非零元素分布没有不论什么规律，所以在进行压缩存储的时侯须要存储非零元素值的同一时候还要存储非零元素在矩阵中的位置，即非零元素所在的行号和列号，也就是在存储某个元素比方aij的值的同一时候，还须要存储该元素所在的行号i和它的列号j，这样就构成了一个三元组(i,j,aij)的线性表。
　　三元组能够採用顺序表示方法，也能够採用链式表示方法，这样就产生了对稀疏矩阵的不同压缩存储方式。

a、稀疏矩阵的顺序实现

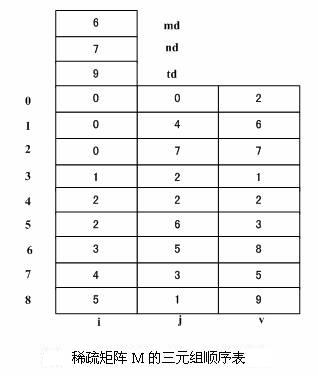
　　若把稀疏矩阵的三元组线性表按顺序存储结构存储，则称为稀疏矩阵的三元组顺序表。
　　顺序表中除了存储三元组外，还应该存储矩阵行数、列数和总的非零元素数目，这样才干唯一的确定一个矩阵。

　　　　

　　顺序存储结构存储三元组线性表的C#代码例如以下：

代码
    struct tupletype<T>
    {
        public int i;//行号
        public int j;//列号
        public T v; //元素值
        public tupletype(int i, int j, T v)
        {
            this.i = i;
            this.j = j;
            this.v = v;
        }
    }
    class spmatrix<T>
    {
        int MAXNUM;//非零元素的最大个数
        int md;//行数值
        int nd;//列数值
        int td;//非零元素的实际个数
        tupletype<T>[] data;//存储非零元素的值及一个表示矩阵行数、列数和总的非零元素数目的特殊三元组
    }
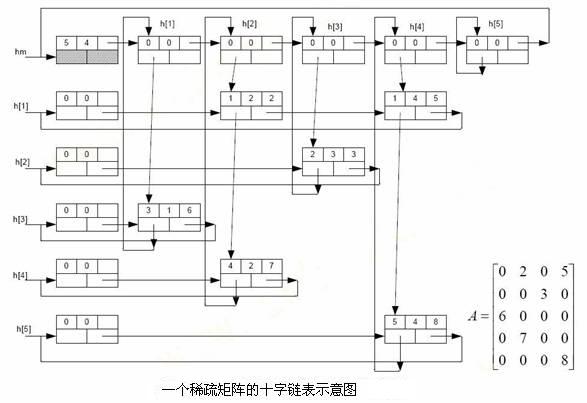
b、稀疏矩阵的十字链表实现

　　　　十字链表结点分为三类 :
　　表结点，它由五个域组成，当中i和j存储的是结点所在的行和列，right和down存储的是指向十字链表中该结点全部行和列的下一个结点的指针，v用于存放元素值。
　　行头和列头结点，这类结点也有域组成，当中行和列的值均为零，没有实际意义，right和down的域用于在行方向和列方向上指向表结点，next用于指向下一个行或列的表头结点。
　　总表头结点，这类结点与表头结点的结构和形式一样，仅仅是它的i和j存放的是矩阵的行和列数。

　　　　

　　十字链表能够看作是由各个行链表和列链表共同搭建起来的一个综合链表，每一个结点aij既是处在第i行链表的一个结点，同一时候也是处在第j列链表上的一个结点，就你是处在十字交叉路口上的一个结点一样，这就是十字链表的由来。
　　十字链表中的每一行和每一列链表都是一个循环链表，都有一个表头结点。
　　　　
三、稀疏矩阵的实现

　　矩阵运算通常包含矩阵转置、矩阵加、矩阵乘、矩阵求逆等。这里仅讨论最简单的矩阵转置运算算法。
　　矩阵转置运算是矩阵运算中最重要的一项，它是将m×n的矩阵变成另外一个n×m的矩阵，使原来矩阵中元素的行和列的位置互换而值保持不变，即若矩阵N是矩阵M的转置矩阵，则有：M[i][j]=N[j][i] (0≤i≤m-1,0≤j≤n-1)。

三元组表表示转置矩阵的详细方法是：
　　第一步：依据M矩阵的行数、列数和非零元总数确定N矩阵的列数、行数和非零元总数。
　　第二步：当三元组表非空（M矩阵的非零元不为0）时，对M中的每一列col(0≤col≤n-1)，通过从头至尾扫描三元组表data，找出全部列号等于col的那些三元组，将它们的行号和列号互换后依次放人N的data中，就可以得到N的按行优先的压缩存贮表示。

代码
    class spmatrix<T>
    {
        int MAXNUM;//非零元素的最大个数
        int md;//行数值
        int nd;//列数值
        int td;//非零元素的实际个数
        tupletype<T>[] data;//存储非零元素的值及一个表示矩阵行数、列数和总的非零元素数目的特殊三元组
        public int Md
        {
            get
            {
                return md;
            }
            set
            {
                md = value;
            }
        }
        public int Nd
        {
            get
            {
                return nd;
            }
            set
            {
                nd = value;
            }
        }
        public int Td
        {
            get
            {
                return td;
            }
            set
            {
                td = value;
            }
        }
        //三元组表的data属性
        public tupletype<T>[] Data
        {
            get
            {
                return data;
            }
            set
            {
                data = value;
            }
        }
        //初始化三元组顺序表
        public spmatrix() { }
        public spmatrix(int maxnum, int md, int nd)
        {
            this.MAXNUM = maxnum;
            this.md = md;
            this.nd = nd;
            data = new tupletype<T>[MAXNUM];
        }
        //设置三元组表元素的值
        public void setData(int i, int j, T v)
        {
            data[td] = new tupletype<T>(i, j, v);
            td++;
        }
        //矩阵转置算法
        public spmatrix<T> Transpose()
        {
            spmatrix<T> N = new spmatrix<T>();
            int p, q, col;
            N.MAXNUM = MAXNUM;
            N.nd = md;
            N.md = nd;
            N.td = td;
            N.data = new tupletype<T>[N.td];
            if (td != 0)
            {
                q = 0;//控制转置矩阵的下标
                for (col = 0; col < nd; col++)//扫描矩阵的列
                {
                    for (p = 0; p < td; p++)//p控制被转置矩阵的下标
                    {
                        if (data[p].j == col)
                        {
                            N.data[q].i = data[p].j;
                            N.data[q].j = data[p].i;
                            N.data[q].v = data[p].v;
                            q++;
                        }
                    }
                }
            }
            return N;
        }

 

本文来自CSDN博客，转载请标明出处：http://blog.csdn.net/zhongjiekangping/archive/2010/05/13/5585933.aspx