图像处理之相似图片识别（直方图应用篇）

算法概述：

首先对源图像与要筛选的图像进行直方图数据采集，对采集的各自图像直方图进行归一化再

使用巴氏系数算法对直方图数据进行计算，最终得出图像相似度值，其值范围在[0, 1]之间

0表示极其不同，1表示极其相似（相同）。

 

算法步骤详解：

大致可以分为两步，根据源图像与候选图像的像素数据，生成各自直方图数据。第二步：使

用第一步输出的直方图结果，运用巴氏系数（Bhattacharyya coefficient）算法，计算出相似程

度值。

 

第一步：直方图计算

直方图分为灰度直方图与RGB直方图，对于灰度图像直方图计算十分简单，只要初始化一

个大小为256的直方图数组H，然后根据像素值完成频率分布统计，假设像素值为124，则

H[124] += 1, 而对于彩色RGB像素来说直方图表达有两种方式，一种是单一直方图，另外一

种是三维直方图，三维直方图比较简单明了，分别对应RGB三种颜色，定义三个直方图HR,

HG, HB, 假设某一个像素点P的RGB值为(4, 231,129), 则对于的直方图计算为HR[4] += 1,

HG[231] += 1, HB[129] += 1, 如此对每个像素点完成统计以后，RGB彩色直方图数据就生成了。

而RGB像素的单一直方图SH表示稍微复杂点，每个颜色的值范围为0 ~ 255之间的，假设

可以分为一定范围等份，当8等份时，每个等份的值范围为32， 16等份时，每个等份值范

围为16，当4等份时候，每个等份值的范围为64，假设RGB值为(14, 68, 221), 16等份之

后，它对应直方图索引值(index)分别为: (0, 4, 13), 根据计算索引值公式:index = R + G*16 + B*16*16

 

对应的直方图index = 0 + 4*16 + 13 * 16 * 16， SH[3392] += 1

如此遍历所有RGB像素值，完成直方图数据计算。

 

第二步：巴氏系数计算，计算公式如下：

 

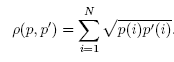
其中P, P’分别代表源与候选的图像直方图数据，对每个相同i的数据点乘积开平方以后相加

得出的结果即为图像相似度值（巴氏系数因子值），范围为0到1之间。

程序效果：

相似度超过99%以上，极其相似

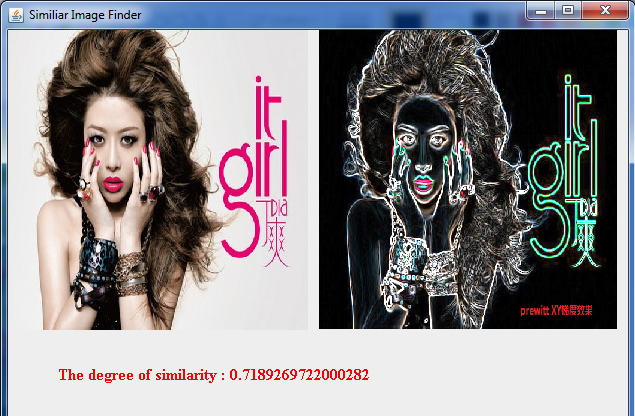
相似度为：72%， 一般相似

程序直方图计算源代码如下：

 

public void setGreenBinCount(int greenBinCount) {
    this.greenBins = greenBinCount;
}

public void setBlueBinCount(int blueBinCount) {
    this.blueBins = blueBinCount;
}

public float[] filter(BufferedImage src, BufferedImage dest) {
    int width = src.getWidth();
       int height = src.getHeight();

       int[] inPixels = new int[width*height];
       float[] histogramData = new float[redBins * greenBins * blueBins];
       getRGB( src, 0, 0, width, height, inPixels );
       int index = 0;
       int redIdx = 0, greenIdx = 0, blueIdx = 0;
       int singleIndex = 0;
       float total = 0;
       for(int row=0; row<height; row++) {
        int ta = 0, tr = 0, tg = 0, tb = 0;
        for(int col=0; col<width; col++) {
            index = row * width + col;
            ta = (inPixels[index] >> 24) & 0xff;
               tr = (inPixels[index] >> 16) & 0xff;
               tg = (inPixels[index] >> 8) & 0xff;
               tb = inPixels[index] & 0xff;
               redIdx = (int)getBinIndex(redBins, tr, 255);
               greenIdx = (int)getBinIndex(greenBins, tg, 255);
               blueIdx = (int)getBinIndex(blueBins, tb, 255);
               singleIndex = redIdx + greenIdx * redBins + blueIdx * redBins * greenBins;
               histogramData[singleIndex] += 1;
               total += 1;
        }
       }

       // start to normalize the histogram data
       for (int i = 0; i < histogramData.length; i++)
       {
        histogramData[i] = histogramData[i] / total;
       }

       return histogramData;
}

计算巴氏系数的代码如下：

 

 

/**
 * Bhattacharyya Coefficient
 * http://www.cse.yorku.ca/~kosta/CompVis_Notes/bhattacharyya.pdf
 *
 * @return
 */
public double modelMatch() {
    HistogramFilter hfilter = new HistogramFilter();
    float[] sourceData = hfilter.filter(sourceImage, null);
    float[] candidateData = hfilter.filter(candidateImage, null);
    double[] mixedData = new double[sourceData.length];
    for(int i=0; i<sourceData.length; i++ ) {
        mixedData[i] = Math.sqrt(sourceData[i] * candidateData[i]);
    }

    // The values of Bhattacharyya Coefficient ranges from 0 to 1,
    double similarity = 0;
    for(int i=0; i<mixedData.length; i++ ) {
        similarity += mixedData[i];
    }

    // The degree of similarity
    return similarity;
}