灰色预测+支持向量机预测财政收入
本案例按照1994年我国财政体制改革后至2013年的数据进行分析并预测未来两年财政收入变化情况。主要按照财政收入分析预测模型流程进行
原始数据为1995年至2015年企业的13个特征与企业年财政收入的数据
相关性分析是指对两个或多个具备相关型的特征元素进行分析,从而衡量两个特征因素的相关密切程度。在统计学中,常用到Pearson相关系数来进行相关性分析。Pearson相关系数可用来度量两个特征间的相互关系(线性相关强弱),是最简单的一种相关系数,常用r或ρ来表示,取值范围在[-1,1],Pearson相关系数的一个关键特性就是,他不会随着特征的位置会是大小变化而变化
代码实现:
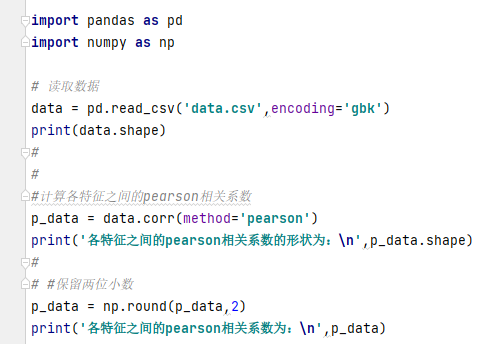
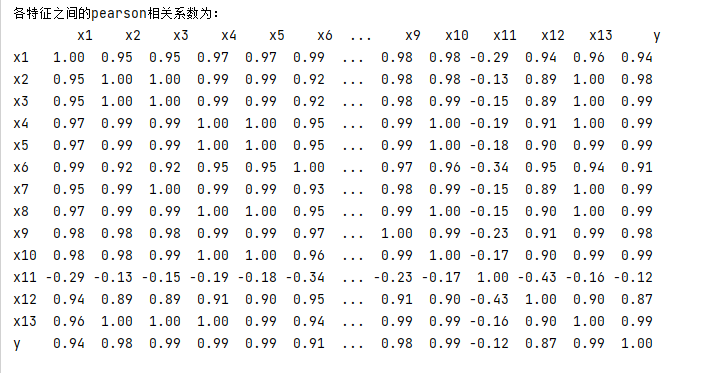
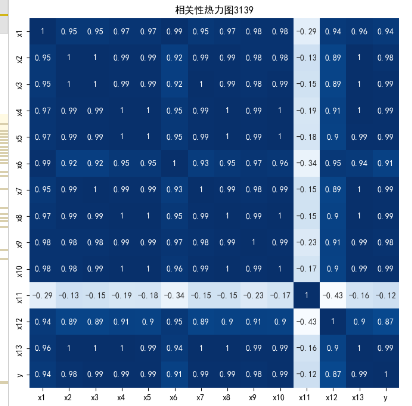
得出pearson的相关系数矩阵为
为了更直观的显示各个特征之间的关系
代码:
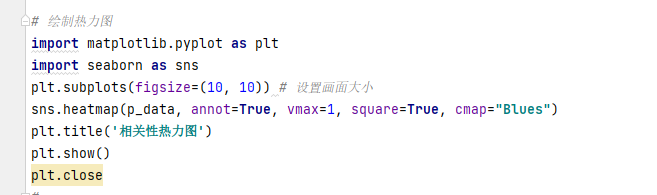
得到图:
数据探索性分析时引入的特征太多,要直接利用其建模,需要进一步的筛选特征,在这里我们采用最近广泛使用的Lasso特征选择方法进一步筛选特征。
Lasso回归方法属于正则化方法的一种,是压缩估计通过构造一个惩罚函数得到一个较为精炼的模型。使用它压缩一些系数,同时设定一些系数为0,保留了子集收缩的有点,是一种处理具有复共线性数据的有偏估计。(有偏估计(biased estimate)是指由样本值求得的估计值与待估参数的真值之间有系统误差,其期望值不是待估参数的真值。)
代码如下:
步骤如下:
首先用Lasso函数求出各个特征与财政收入的相关系数


可以得出有五个相关系数为0的特征,接下来将这五个特征从预测数据中去除,将新数据导入新的文件
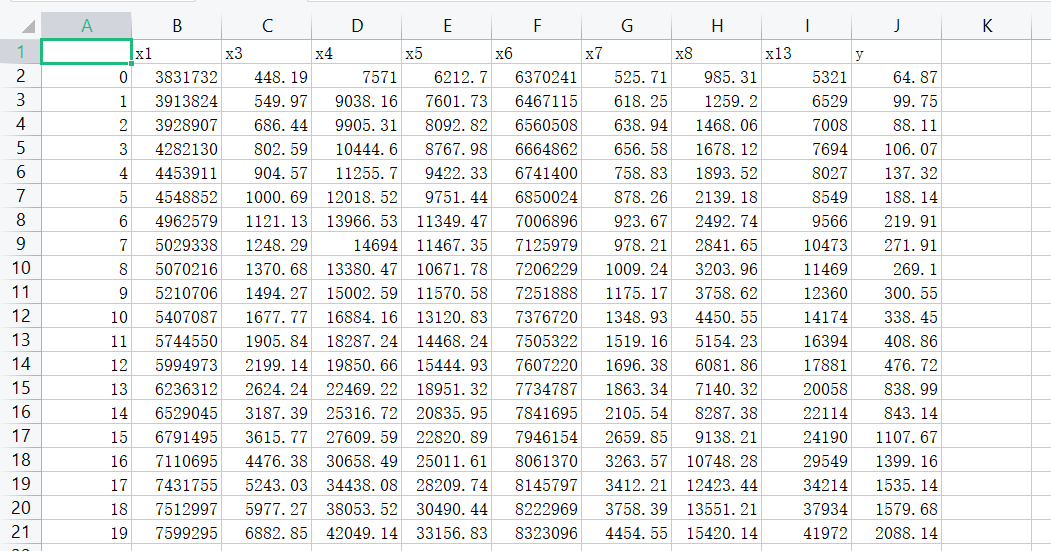
基于灰色预测对小样本数据集的优良性能,首先对单个特征建立灰色预测模型,得到各特征2014-2016年的预测值。然后对2013年以前的训练数据建立支持向量回归预测模型,将建立好的模型与灰色预测模型结合,对2014和2016年的财政收入进行预测。
代码如下:
自编灰色预测模型函数

代码实现预测:
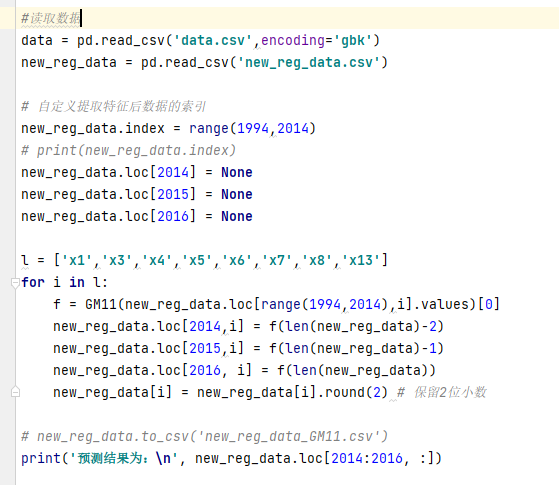
预测结果为:
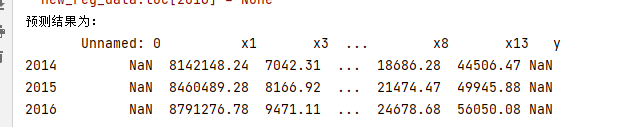
#用支持向量机来预测2014-2016的财政收入
from sklearn.svm import LinearSVR
import matplotlib.pyplot as plt
from sklearn.metrics import explained_variance_score,mean_absolute_error,mean_squared_error,median_absolute_error,r2_score
data = pd.read_csv('new_reg_data.csv',index_col=0) #读取文件是设定第一列为索引,否则默认为0开始,后面会报错找不到索引
feature = ['x1','x3','x4','x5','x6','x7','x8','x13']
print(data)
# 取2014年之前的数据建模
data_train = data.iloc[range(1994,2014)].copy()
data_std = data_train.std() # 取标准差
data_mean = data_train.mean() # 取平均值
data_train = (data_train - data_mean)/data_std # 数据标准化
print(data_train.columns)
#Index(['Unnamed: 0.1', 'x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13', 'y '], dtype='object')
x_train = data_train[feature].values # 特征数据
y_train = data_train['y'].values # 标签数据
linearsvr = LinearSVR().fit(x_train,y_train)
x = ((data[feature]-data_mean[feature])/data_std[feature]).as_matrix() #预测,并还原结果
linearsvr = LinearSVR().fit(x_train,y_train)
x = ((data[feature]-data_mean[feature])/data_std[feature]).as_matrix() #预测,并还原结果
data[u'y_pred'] = linearsvr.predict(x)*data_std['y'] + data_mean['y']
#SVR预测后保存的结果
#data.to_excel('tmp/new_reg_data_GM11_revenue.xls')
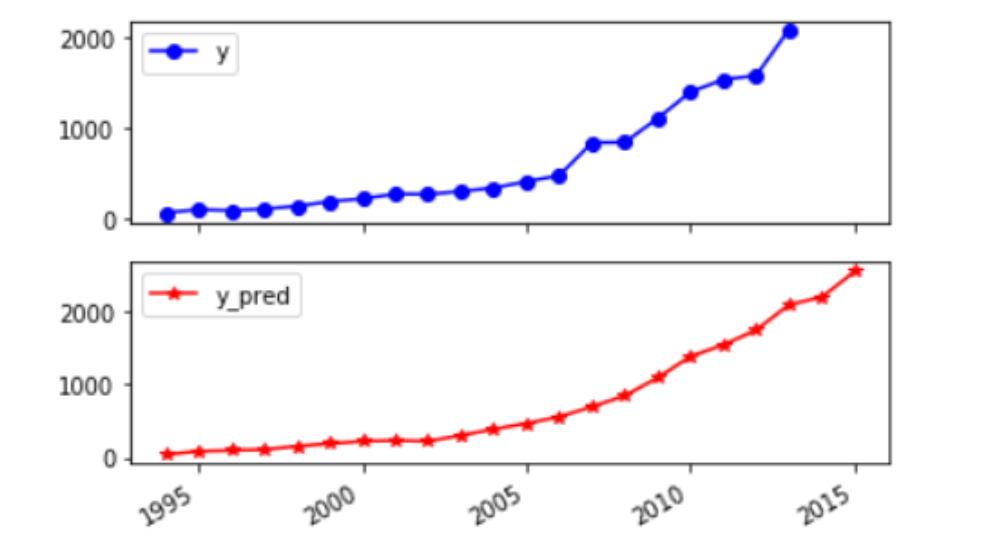
print('真实值与预测值分别为:\n',data[['y','y_pred']])
print('预测图为:',data[['y','y_pred']].plot(subplots = True,
style=['b-o','r-*']))
结果为: