python画图学习

python基本绘图函数学习

1.plot绘制线型图

plot是python中最基本的绘制二维线性折线图的函数

基本使用方式：plt.plot(x,y,s)

代码实现：

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#plt.plot(x,y,s)   画出红色的正弦函数图
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0,2*np.pi,50)  #绘制出50个横坐标   (0,2Π)
y = np.sin(x)
plt.title('3139')
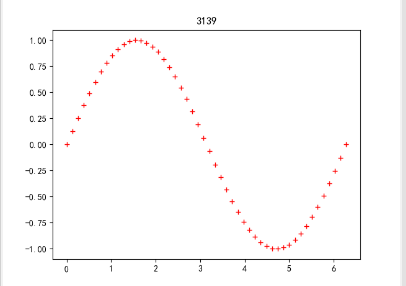
plt.plot(x,y,'r+')
plt.show()

实现结果

 

 

2.pie函数绘制饼图

饼图能够展示出各个部分的比例，能够非常只管的感受出每个部分的占比

代码实现：

import matplotlib.pyplot as plt

labels = ['数学','专业课','英语','政治']
sizes = [40,40,10,10]   #每一块的比例
colors =['yellowgreen','gold','lightskyblue','lightcoral']   #每一块的颜色
explode = (0.2,0.1,0,0)    #突出显示

plt.pie(sizes,explode=explode,labels=labels,colors=colors,autopct='%1.1f%%',shadow=True,startangle=90)
plt.axis('equal')      #显示为圆，避免压缩成椭圆
plt.title('3139')
plt.show()
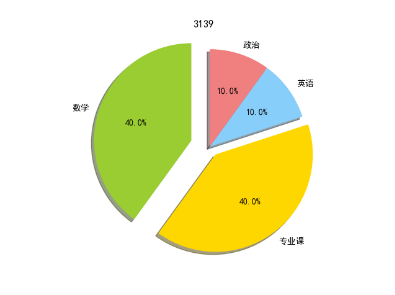
运行结果

 

 

这里以考研为例子，数学与专业课将要占掉复习时间的大头，而政治和英语所花的时间要稍微少一些，还可以观察到数学的的部分更加突出（离圆心更远），这是因为数学是最能够
拉开分数的一门。

3.hist函数绘制二位条形直方图

代码实现：

# x = np.random.randn(1000)   #随机生成1000个服从正态分布的随机数
# plt.hist(x,10)
# plt.title('3139')
# plt.show()
#
# import pandas as pd
# data = pd.read_excel("catering_sale.xls",index_col='日期')   #读取数据，置顶日期为索引列
# data = data['销量']
# plt.hist(data,10)
# plt.title('3139')
# plt.show()

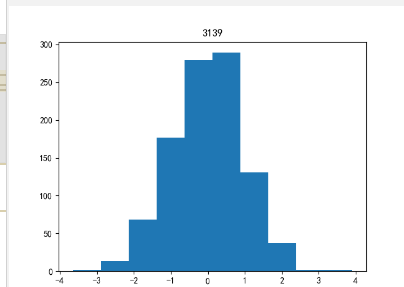
运行结果

 直方图可以很好的观察数据的分布特征，这里用python的np.random.randn(1000)绘制了一千个服从正态度分布的数，为了更为明显我运行了三次，直方图都是服从正态分布的

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.boxplot绘制箱型图

箱型图可以很明显的看出异常值，异常值都被清晰的标志出来

实现代码1

#绘制箱型图
x = np.random.randn(1000)
D= pd.DataFrame([x,x+1]).T     #构造两列的DataFrame
D.plot(kind='box')       #Series内置绘图方法，指定参数为box
plt.title('3139')
#用annotate添加注释
plt.show()

运行结果

 

 

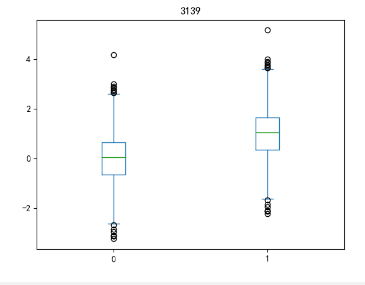
 可以看出小黑点就是离群点

 

这里再用一个本书上的例子来画一个箱型图

import pandas as pd
import numpy as np

data = pd.read_excel("catering_sale.xls",index_col='日期')   #读取数据，置顶日期为索引列
print(data.describe())


#餐饮日销售额异常值检测
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

plt.figure()    #建立图像
p = data.boxplot(return_type='dict')
x = p['fliers'][0].get_xdata()        #fliers即为异常值的标签
y = p['fliers'][0].get_ydata()
y.sort()


#用annotate添加注释
for i in range(len(x)):
    if i>0:
        plt.annotate(y[i],xy = (x[i],y[i]),xytext = (x[i]+0.05 - 0.8/(y[i]-y[i-1]),y[i]))
    else:
        plt.annotate(y[i],xy = (x[i],y[i]),xytext=(x[i]+0.08,y[i]))

plt.show()

运行结果

 

 

 

数据为某餐饮公司日期与对应日销售额的数据，可以很清晰的看出离群点已经被显示出来，这里可以将离得比较近的4065 4060  865与归为正常值

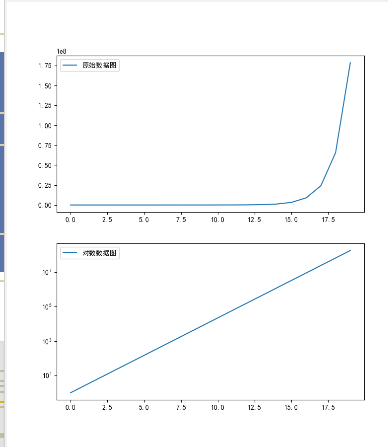
5.plot(logx=True)/plot(logy=True) 绘制对数图

代码实现

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

x = pd.Series(np.exp(np.arange(20)))
plt.figure(figsize=(8,9))
ax1 = plt.subplot(2,1,1)
x.plot(label='原始数据图',legend=True)

ax1 = plt.subplot(2,1,2)
x.plot(logy=True,label='对数数据图',legend=True)
plt.show()

运行结果

 

 

总结：图像虽说和基本，但都是常用来分析数据规律的图，简单且实用，通过画这几个图我懂得了每个图都能表示出数据的什么特征，
在之后数据分析的学习我能够更快的想到要用什么图