通过sin(1/x)的可积性讨论可积与收敛的联系

 已知f(x) available 

before wo look the four  questions,we should know the distinction between n and x,n means the points is discrete,but x means continuous.

so for A,it is obviously that the former is weaker.

 但是严格来讲，我们需要用反例去证明错误。这里老师举得是sin（1/x），取xn=1/nΠ，此时f（xn）为nΠ，一直都是正整数，A=0，条件成立

但是对于

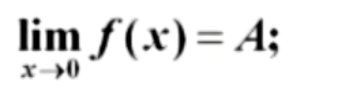
 我们知道在趋于0，是震荡的，所以不成立，此为反例。

ps：这里有争议点的是sin（1/x）在在趋于0的点不是震荡的吗？是否可积呢？

由于是奇函数，所以我们只看（0，+∞）

已知，在（1，+∞），函数有界，取值范围-1 1

在该区间函数是有限个周期的波条，因此积分是收敛的（收敛意味着积分值在极限意义下是有限的，因此收敛）

在（0，1）

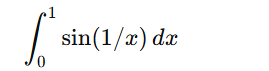
 令u=1/x，变为

 判断其收敛性，sinu有界

 

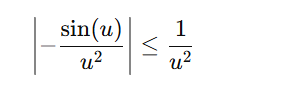
因而是收敛的，综上所述，该积分是收敛的。

那么收敛和可积又有什么联系呢？

可积性，意味着我们可以计算在该区间的定积分，并且该积分有一个有限的取值

收敛性，在讨论积分时，收敛性通常指无穷积分或不定积分的收敛，即意味着该值在极限意义下是有限的。

1、有限区间上的可积性：有限闭区间，函数可积，积分一定是有限的

2、无穷区间的上的可积性，如果收敛，那么函数在该区间上是可积的。