【死亡小学期第一章：命运大转盘】希尔排序 | 图 | 树 | 公交线路提示
希尔排序
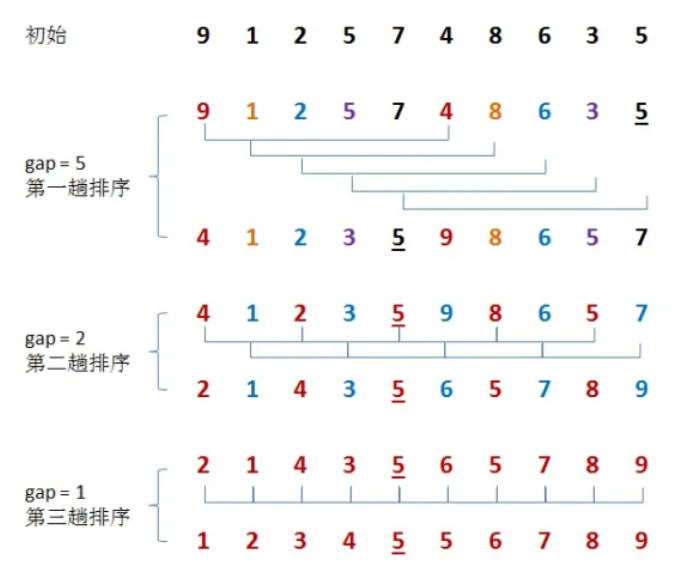
通过不断缩小·基数进行每个基数长度的插入排序。
递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法，因为前面的排序与后面的排序无关。
稳定排序：在排序过程中，如果两个键的值相同，那么他们的相对位置不发生变化。不符合该规则的排序算法不是稳定排序算法。
题目
本题要求实现一趟希尔排序函数，待排序列的长度1<=n<=1000。
函数接口定义：
void ShellInsert(SqList L,int dk);
其中L是待排序表，使排序后的数据从小到大排列。
类型定义
typedef int KeyType;
typedef struct {
KeyType *elem; /*elem[0]一般作哨兵或缓冲区*/
int Length;
}SqList;
裁判测试程序样例：
#include<stdio.h>
#include<stdlib.h>
typedef int KeyType;
typedef struct {
KeyType *elem; /*elem[0]一般作哨兵或缓冲区*/
int Length;
}SqList;
void CreatSqList(SqList *L);/*待排序列建立，由裁判实现，细节不表*/
void ShellInsert(SqList L,int dk);
void ShellSort(SqList L);
int main()
{
SqList L;
int i;
CreatSqList(&L);
ShellSort(L);
for(i=1;i<=L.Length;i++)
{
printf("%d ",L.elem[i]);
}
return 0;
}
void ShellSort(SqList L)
{
/*按增量序列dlta[0…t-1]对顺序表L作Shell排序,假设规定增量序列为5,3,1*/
int k;
int dlta[3]={5,3,1};
int t=3;
for(k=0;k<t;++k)
ShellInsert(L,dlta[k]);
}
/*你的代码将被嵌在这里 */
输入样例：
第一行整数表示参与排序的关键字个数。第二行是关键字值 例如：
10
5 2 4 1 8 9 10 12 3 6
输出样例：
输出由小到大的有序序列，每一个关键字之间有空格隔开，最后一个关键字后有一个空格。
1 2 3 4 5 6 8 9 10 12
哨兵
只要存在“邻居依赖”的地方，就可以考虑使用哨兵。
哨兵是用来简化边界问题的虚设对象。
答案
void ShellInsert(SqList L,int dk){ for(int i=dk+1;i<=L.Length;i++){//elem[0]是哨兵 if(L.elem[i-dk]>L.elem[i]){//判断大小 L.elem[0]=L.elem[i-dk];//利用哨兵来交换位置 L.elem[i-dk]=L.elem[i]; L.elem[i]=L.elem[0]; i=dk+1;//移动位置 } } }
图
题目
7-2 关键路径
假定一个工程由若干子任务构成，使用一个包含n个顶点、e条边的AOE网表示该工程，顶点编号为1至n，有向边表示该工程的每个子任务，边的权值表示完成该子任务所需的时间，假定网中只含一个源点和一个汇点。请编写程序求出该工程的所有关键活动，并计算完成该工程所需的最短时间。
输入格式:
每个测试点包含多组测试数据。每组数据第一行为2个整数n和e，均不超过200，分别表示AOE网的顶点数和边数。接下来e行表示每条边的信息，每行为3个正整数a、b、c，其中a和b表示该边的端点编号，c表示权值。各边并不一定按端点编号顺序排列，且各顶点并不一定按拓扑序排列。
输出格式:
对每组数据，若工程不可行（AOE网中存在环），输出“unworkable project”；若工程可行，则输出第一行为完成工程所需的最短时间，并从第2行开始输出关键活动，每个关键活动占一行，格式为i->j，其中i和j表示关键活动所在边的端点编号。各关键活动输出顺序为：按i的递增顺序输出，若多个关键活动的i值相同，则按j的递增顺序输出。
输入样例:
4 4
1 2 6
1 3 4
2 4 1
3 4 1
输出样例:
7
1->2
2->4C库函数 - memset()
void *memset(void *str, int c, size_t n)
str -- 指想要被填充的内存块
c -- 要被设置的值。该值以int形式传递，但是函数在填充内存块时是使用该值的无符号字符形式。
n -- 要被设置为该值的字符数。
该值返回一个指向存储区str的指针。
举例
#include <stdio.h> #include <string.h> int main () { char str[50]; strcpy(str,"This is string.h library function"); puts(str); memset(str,'$',7); puts(str); return(0); }
This is string.h library function $$$$$$$ string.h library function
0x3f
1、作为无穷大使用
2、可以保证无穷大加无穷大仍然不会超限
memset函数是对字节为单位进行赋值的；
void *memset(void *s, int ch, size_t n);
函数解释：将s中前n个字节 （typedef unsigned int size_t ）用 ch 替换并返回 s 。
其实这里面的ch就是ascii为ch的字符；
将s所指向的某一块内存中的前n个 字节的内容全部设置为ch指定的ASCII值
拓扑排序
介绍
将一个有向无环图进行拓扑排序，使得图中所有顶点排成一个线性序列。
拓扑排序对应施工的流程图具有特别重要的作用，它可以决定哪些子工程必须要先执行，哪些子工程要在某些工程执行后才可以执行。
简称AOV网，即不应该带有回路，因为若带有回路，则回路上的所有活动都无法进行，对于数据流来说就是死循环。
实现步骤
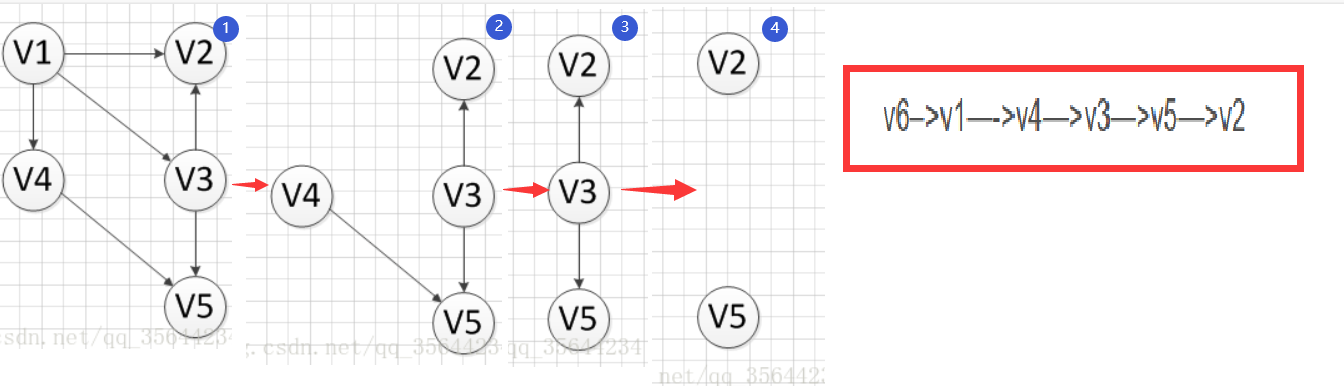
1、在有向图中选一个没有前驱的顶点并且输出
2、从图中删除该顶点和所有以它为尾的弧。（删除所有和它有关的边）
3、重复上述两步，直至所有顶点输出，或者当前图中不存在无前驱的顶点为止
若在带权的有向无环图中，以顶点表示事件，以有向边表示活动，边上的权值表示活动的开销（如该活动持续的时间），则此带权的有向无环图称为AOE网。
记住AOE-网只是比AOV-网多了一个边的权重，而且AOV-网一般是设计一个庞大的工程各个子工程实施的先后顺序，而我们的AOE-网就是不仅仅关系整个工程中各个子工程的实施的先后顺序，同时也关系整个工程完成最短时间。
AOE-网还有一个特点：只有一个起点（入度为0的顶点）和一个终点（出度为0的顶点）
并且AOE-网有两个待研究的问题：
- 完成整个工程需要的时间
- 哪些活动是影响工程进度的关键
求关键路径的步骤
1、输入顶点数和边数，以及各个弧的信息建立图
2、从源点v1出发，令ve[0]=0;按照拓扑序列往前求各个顶点的ve。如果得到的拓扑序列个数小于网的顶点数n，说明我们建立的图有环，无关键路径，直接结束程序
3、从终点vn出发，令vl[n-1]=ve[n-1]，按逆拓扑序列，往后求其他顶点vl值
4、根据各个顶点的ve和vl求每个弧的e（i）和l（i），如果满足e（i）=l（i），说明是关键活动。
公交线路提示
所选题目
建立石家庄市主要公交线路图，实现多样化的信息查询功能。
基本要求：
(1) 查询公交站点的基本信息，公交站点信息包括公交站点名称，地理位置坐标，公交线路信息等；
(2) 查询公交线路的基本信息，公交线路信息包括公交线路名称，沿途公交站点信息等；
(3) 输入任意两站点，给出最佳的乘车线路和转车地点。如：该城市共有n条公交线路，m个公交站点。其中，公交线路1经过编号为1，2，4，7的站点，公交线路2经过编号为3，5，7，8，的站点，则从站点2到站点8的最佳乘车线路是：乘坐公交线路1从站点2到站点7再乘坐公交线路2到站点8。
思路整理及信息收集
pkl文件的优点——pickle序列化（字节流）
当大量数据的时候，保存成pkl序列化文件的格式，能够加快python的读写速度。
功能：把你上次计算得到的数据保存起来，当你需要使用这些数据的时候，直接通过load将数据进行恢复：
1、不需要重新去计算得到的数据，节省计算机资源。
2、不需要经过数据格式转换，提高效率
3、pickle可以保存多个对象。实验中，同一数据集下需要保存的内容不止一种，通过pickle可以全部进行保存到一个.pkl文件。
