《聊聊数据结构与算法》之排序算法-上篇

1、前言

　　数据结构与算法一直作为计算机软件领域的核心基础之一，其在软件编程领域始终发挥着不可或缺的作用。鉴于软件开发以及软件测试的从业者而言，更是一种提升自身能力的重要途径。换句话说，如何让自己的代码写的妙不可言或者快速阅读一些开源代码，享受源代码带来的喜悦与兴奋，我们还是有必要熟悉和掌握数据结构与算法。个人认为，熟知算法不仅惠及于编码工作，也有利于强化逻辑思维能力，是件百利而无一害的学习。因此，闲暇之余我计划写些数据结构与算法系列博文，帮助自己以及有需要的人总结和掌握这方面的知识。其中，关于排序算法我写了上下两篇文章，本文为上篇，另外一篇请朋友们自行查看我的博文清单。

 

2、排序算法体系

　　排序算法基本分为内部排序和外部排序两大类，其中内部排序是指仅在内存中进行的排序，外部排序是指需要依托内存和外存相结合的排序算法，本文主要是探讨内存排序。详细分类如下图所示：

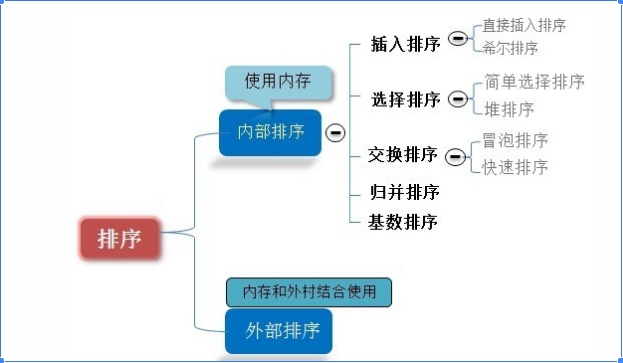
 　　外部排序多指的是大文件的排序，即待排序的记录存储在外存储器上，待排序的文件无法一次装入内存，需要在内存和外部存储器之间进行多次数据交换，以达到排序整个文件的目的。外部排序最常用的算法是多路归并排序，即将原文件分解成多个能够一次性装入内存的部分，分别把每一部分调入内存完成排序。然后，对已经排序的子文件进行多路归并排序。

3、时间与空间复杂度

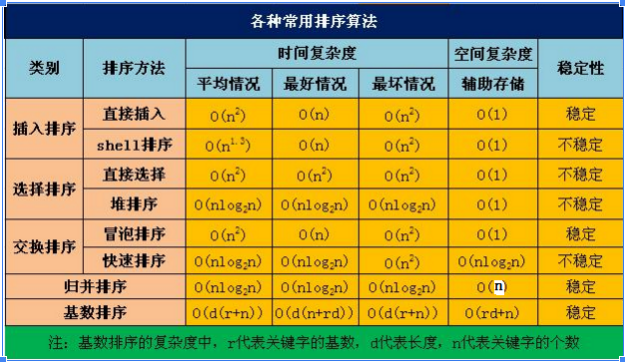
注：

• 所需辅助空间最多：归并排序
• 所需辅助空间最少：堆排序
• 平均速度最快：快速排序
• 不稳定排序：快速排序，直接选择、希尔排序，堆排序。（口诀：快速选择希尔堆是不稳定的，其他都是稳定排序。）
• 桶排序也是稳定的，速度最快（比快排还要快），但是其占用空间最大（基本上是最耗空间的一种排序算法）。
• 向大根堆中插入一个元素：空间复杂度：O（1），时间复杂度：O（log2n）

 

• 排序算法稳定性

　　假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

• 稳定性好处

　　排序算法如果是稳定的，那么从一个键上排序，然后再从另一个键上排序，第一个键排序的结果可以为第二个键排序所用。基数排序就是这样，先按低位排序，逐次按高位排序，低位排序相同的元素其顺序在高位排序中是不会改变的。

 

内部排序

1、插入排序（直接插入排序）

• 算法

　　插入排序（Insertion Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

• 示例

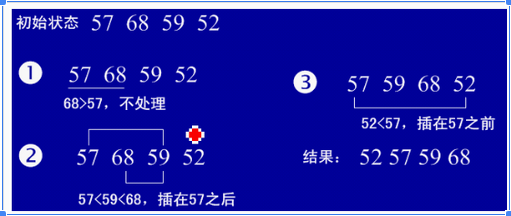
•  实现

 

2、二分插入排序

• 算法

　　二分（折半）插入（Binary insert sort)排序是一种在直接插入排序算法上进行小改动的排序算法。其与直接排序算法最大的区别在于查找插入位置时使用的是二分查找的方式，在速度上有一定提升。

• 步骤

　　一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

• • 从第一个元素开始，该元素可以认为已经被排序
  • 取出下一个元素，在已经排序的元素序列中二分查找到第一个比它大的数的位置
  • 将新元素插入到该位置后
  • 重复上述两步

• 实现

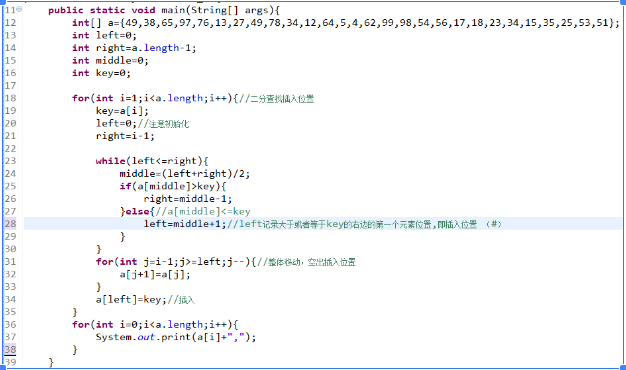
 注：

• 二分插入排序是一种稳定的排序。当n较大时，总排序码比较次数比直接插入排序的最差情况好得多，但比最好情况要差，所元素初始序列已经按排序码接近有序时，直接插入排序比二分插入排序比较次数少。二分插入排序元素移动次数与直接插入排序相同，依赖于元素初始序列。
• 移动位置的分析取决于二分查找的最后一次（需要移动）

 

3、希尔排序（缩小增量排序）

• 算法

　　希尔排序，也称缩小增量排序算法，因DL．Shell于1959年提出而得名，是插入排序的一种高速的改进版本。算法先将要排序的一组数按某个增量d（n/2,n为要排序数的个数）分成若干组，每组中记录的下标相差d.对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。当增量减到1时，进行直接插入排序后，排序完成。

• 步骤

  • 将一组数按照序号增量进行划分成若干组。
  • 每组中按照直接插入排序。
  • 缩小序号增量（序号增量d按照：d/2,并且取奇数），继续划分并插入排序；
  • 直到序号增量为1，排序完成。

• 示例

 

•  实现

 

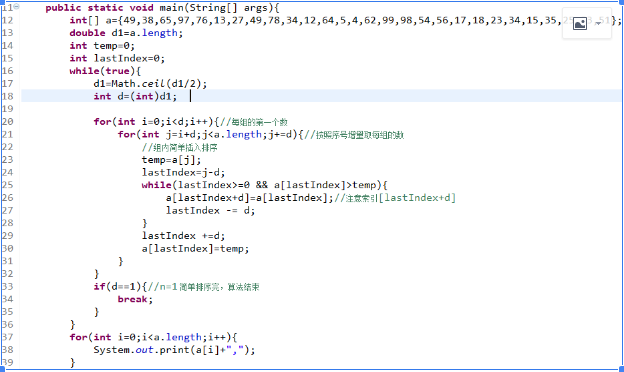
4、选择排序（简单选择排序）

• 算法

　　选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
　　换句话说，在要排序的一组数中，选出最小的一个数与第一个位置的数交换；然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。

• 示例

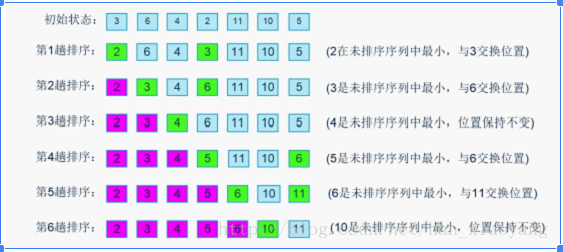
•  实现

 

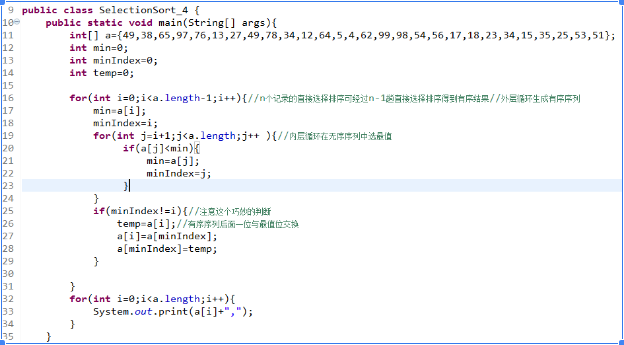
5、冒泡排序

• 算法

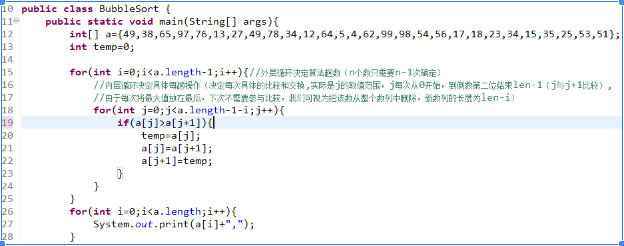
　　冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端。

• 示例

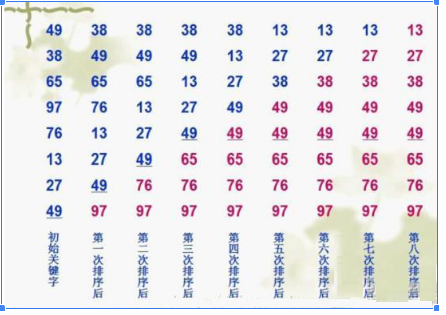
•  实现

 

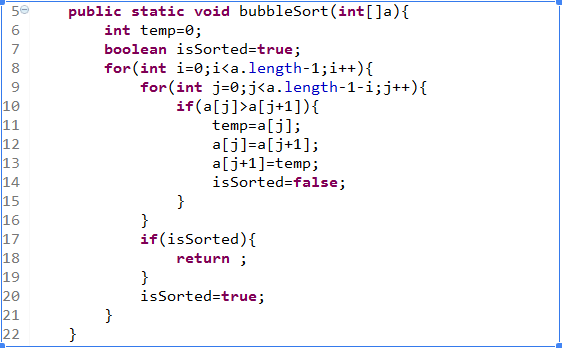
•  改进

  （如果某趟没有发生交换，则该数列已经是有序，直接返回或者跳出）

 

 

6、鸡尾酒排序/双向冒泡排序

• 算法

 ①术语

②　

　　要是文艺点的话，可以说是搅拌排序，通俗易懂点的话，就叫“双向冒泡排序”，冒泡是一个单向的从小到大或者从大到小的交换排序，而鸡尾酒排序是双向的，先从一端进行从小到大排序，然后从另一端进行从大到小排序。

•  示例

　　从图中可以看到，第一次正向比较，我们找到了最大值9。
　　第一次反向比较，我们找到了最小值1.
　　第二次正向比较，我们找到了次大值8.
　　第二次反向比较，我们找到了次小值2
　　。。。
　　最后就大功告成了。

• 实现

•  改进

　　当数组有序的时候，我们还会继续往下排，直到完成length/2次，这个就跟没优化之前的冒泡排序一样，此时我们可以加上一个标志位IsSorted来判断是否已经没有交换了，如果没有（则已经有序），提前退出循环。