CMU-15445 LAB2:实现一个支持并发操作的B+树
概述
经过几天鏖战终于完成了lab2,本lab实现一个支持并发操作的B+树。简直B格满满。
B+树
为什么需要B+树
B+树本质上是一个索引数据结构。比如我们要用某个给定的ID去检索某个student记录,如果没有索引的话,我们可能从第一条记录开始遍历每一个student记录,直到找到某个ID和我们给定的ID一致的记录。可想而知,这是非常耗时的。
如果我们已经维护了一个以ID为KEY的索引结构,我们可以向索引查询这个ID对应的记录所在的位置,然后直接从这个位置读取这个记录。从索引查询某个ID对应的位置,这个操作需要高效,B+树能保证以O(log n)的时间复杂度完成。
B+树的性质
B+树由叶子节点和内部节点组成,和其它树结构差不多,但是对(KEY, VALUE)的个数和排列顺序有要求。
叶子节点:
格式如下:
* ---------------------------------------------------------------------------
* | HEADER | KEY(1) + RID(1) | KEY(2) + RID(2) | ... | KEY(n) + RID(n)
* ---------------------------------------------------------------------------
假设叶子结点最多能容纳个n个(KEY, RID)对,那么该叶子节点任何时候都不能少于n/2向上取整个(KEY, RID)对。假设(KEY, RID)对个数为x,那么x必须满足:
ceil(n/2) <= x <= n
ceil表示向上取整,博客园不支持LaTeX o(╯□╰)o。
KEY是search key,RID是该KEY对应的记录的位置。(KEY, RID)对按照KEY的増序进行排列。
HEADER的结构如下:
* ----------------------------------------------------------------------------------------
* | PageType (4) | LSN (4) | CurrentSize (4) | MaxSize (4) | ParentPageId (4) | PageId(4) |
* ---------------------------------------------------------------------------------------
ParentPageId指向父节点。
内部节点
* ----------------------------------------------------------------------------------------
* | HEADER | INVALID_KEY+PAGE_ID(1) | KEY(2)+PAGE_ID(2) | ... | KEY(n)+PAGE_ID(n) |
* ----------------------------------------------------------------------------------------
假设内部节点最多容纳n个(KEY, PAGE_ID)对,和叶子节点一样,x必须满足:
ceil(n/2) <= x <= n
KEY表示search key,PAGE_ID指的是子节点的ID。
(KEY, PAGE_ID)对按照KEY的増序进行排列。
第一个KEY是无效的。
假设PAGE_ID(i)对应的子树中的KEY用SUB_KEY表示,那么SUBKEY都满足:KEY(i) <= SUB_KEY < KEY(i+1)。
查找操作
课本p489给出了find的伪代码。总结来说就是先找到KEY应该出现的叶子节点,然后在该叶子节点中,查找KEY对应的RID。
如下图:
假如我们希望查找的KEY为38,第一步在根节点A查找38应该出现在哪个子节点中,根据之前的性质,38应该出现在以B为根的子树中,继续查找节点B,以此类推,最终38应该出现在H的叶子节点中。最后我们在H中查找38。
所以对于内部节点,我们需要一个Lookup(const KeyType &key,const KeyComparator &comparator)方法,查找key应该出现在哪个子节点对应的子树中。
INDEX_TEMPLATE_ARGUMENTS
ValueType
B_PLUS_TREE_INTERNAL_PAGE_TYPE::Lookup(const KeyType &key,
const KeyComparator &comparator) const {
assert(GetSize() >= 2);
// 先找到第一个array[index].first大于等于key的index(从index 1开始)
int left = 1;
int right = GetSize() - 1;
int mid;
int compareResult;
int targetIndex;
while (left <= right) {
mid = left + (right - left) / 2;
compareResult = comparator(array[mid].first, key);
if (compareResult == 0) {
left = mid;
break;
} else if (compareResult < 0) {
left = mid + 1;
} else {
right = mid - 1;
}
}
targetIndex = left;
// key比array中所有key都要大
if (targetIndex >= GetSize()) {
return array[GetSize() - 1].second;
}
if (comparator(array[targetIndex].first, key) == 0) {
return array[targetIndex].second;
} else {
return array[targetIndex - 1].second;
}
}
因为KEY是已排序的,所以可以先二分查找第一个大于或等于KEY的下标targetIndex,如果targetIndex对应的KEY就是我们要找的KEY,那么targetIndex对应的value就是下一步要搜索的节点,否则targetIndex-1对应的value是下一步应该搜索的节点。
插入操作
课本p494给出了完整的insert(key, value)操作的伪代码。
思路就是:
- 先找到key应该出现的叶子节点,将(key, value)插入到该叶子节点中。
- 如果插入后该叶子节点中键值对超出了最大值,则进行分裂。如果插入后没有超出最大限制,那么就完成任务了。
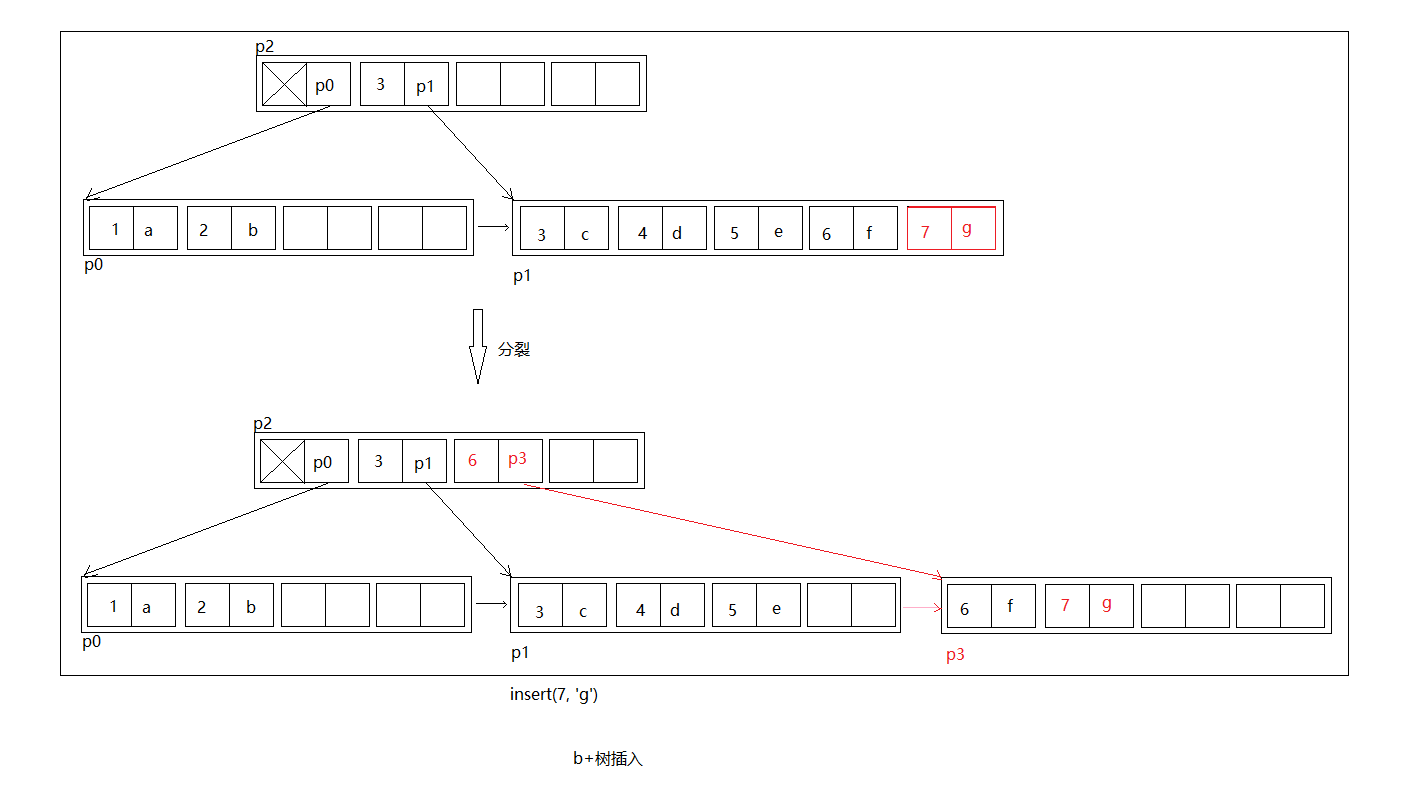
如上图准备插入(7, 'g'),但是插入前p1叶子结点已经满了,那么先插入,然后将插入后的节点,分裂出新的节点p3,将p1原来一半的元素挪到p3,然后将(6, p3)插入到父节点p2中,其中6是新创建的节点p3第一个key。
同样的,如果我们在父节点p2中插入了(6, p3)导致了p2超过最大限制,p2也需要分裂,以此类推,这个过程可能产生新的根节点。
删除操作
课本p498给出了完整的delete(key)操作的伪代码。
思路:
- 先找到key应该出现的叶子节点,删除该叶子节点中key对应的键值对。
- 删除后如果个数少于规定最少个数,那么有两个措施,如果当前节点个数和兄弟节点个数总和不超过允许的最大个数,那么进行并合。否则,从兄弟节点中借一个元素。
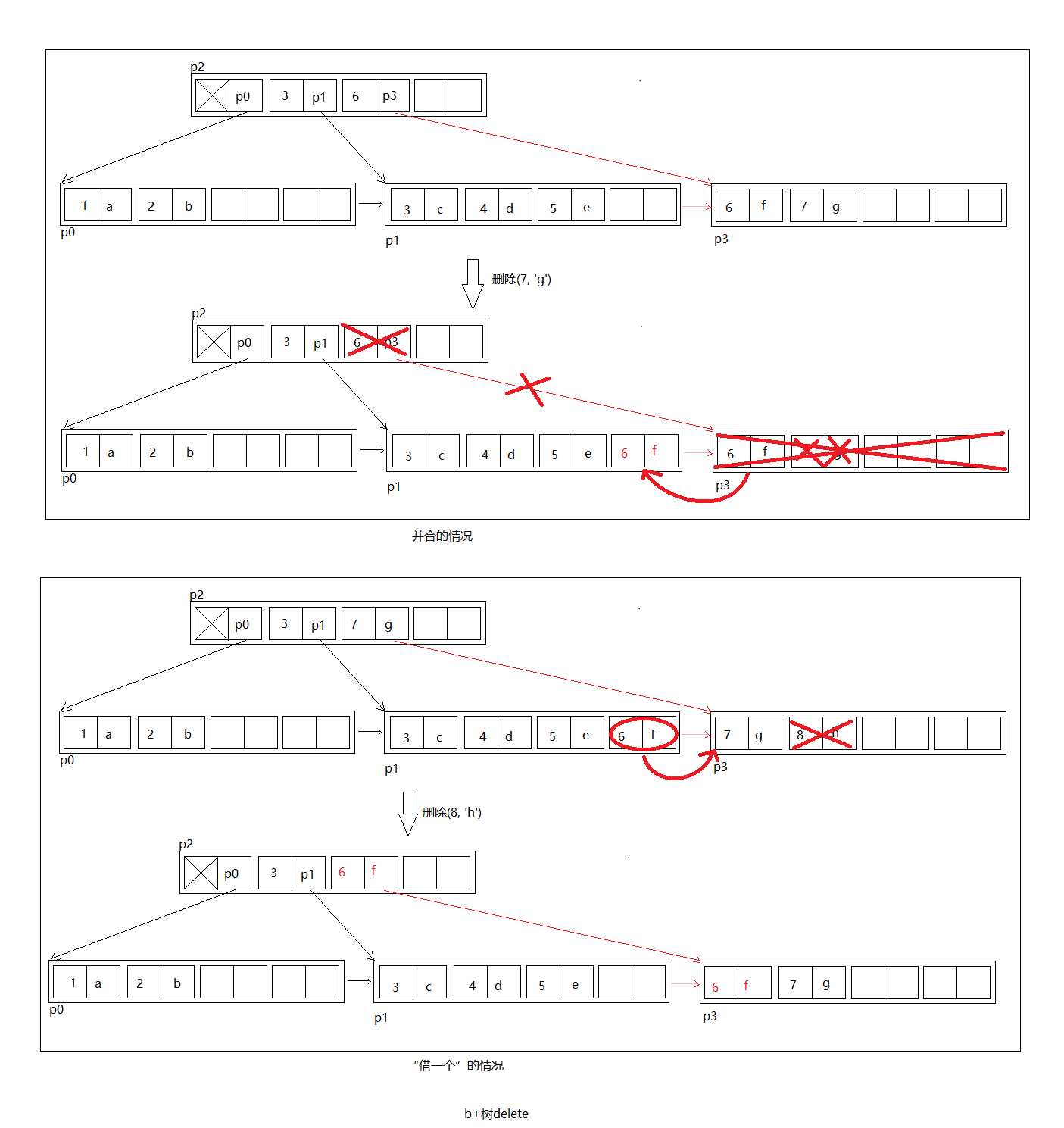
上图第一种情况:
删除(7, 'g')后,p3只有一个元素,少于最少允许的个数(2),于是将(6, 'f')已到兄弟节点p1, 删除p3节点,并且删除父节点p2中的(6, p3),如果p2也少于最少允许个数,递归进行。
第二种请求:
删除p3的(8, 'h')后,p3只有一个元素,于是从兄弟节点p1借一个元素(6, f),然后将父节点(7, 'g')修改为(6, 'f'),这种情况不需要递归。
支持并发操作
最粗暴的方式就是在find, insert, delete开始就加锁,执行完毕后解锁,这样逻辑上没有问题,但是并发效率很低,相当于串行执行。
crabbing协议
该协议允许多个线程同时访问修改B+树。
基本算法
- 对于查询操作,从根节点开始,首先获取根节点的读锁,然后在根节点中查找key应该出现的孩子节点,获取孩子节点的读锁,然后释放根节点的读锁,以此类推,直到找到目标叶子节点,此时该叶子节点获取了读锁。
- 对于删除和插入操作,也是从根节点开始,先获取根节点的写锁,一旦孩子节点也获取了写锁,检查根节点是否安全,如果安全释放孩子节点所有祖先节点的写锁,以此类推,直到找到目标叶子节点。节点安全定义如下:如果对于插入操作,如果再插入一个元素,不会产生分裂,或者对于删除操作,如果再删除一个元素,不会产生并合。
举个查找过程的例子,查找key=38:
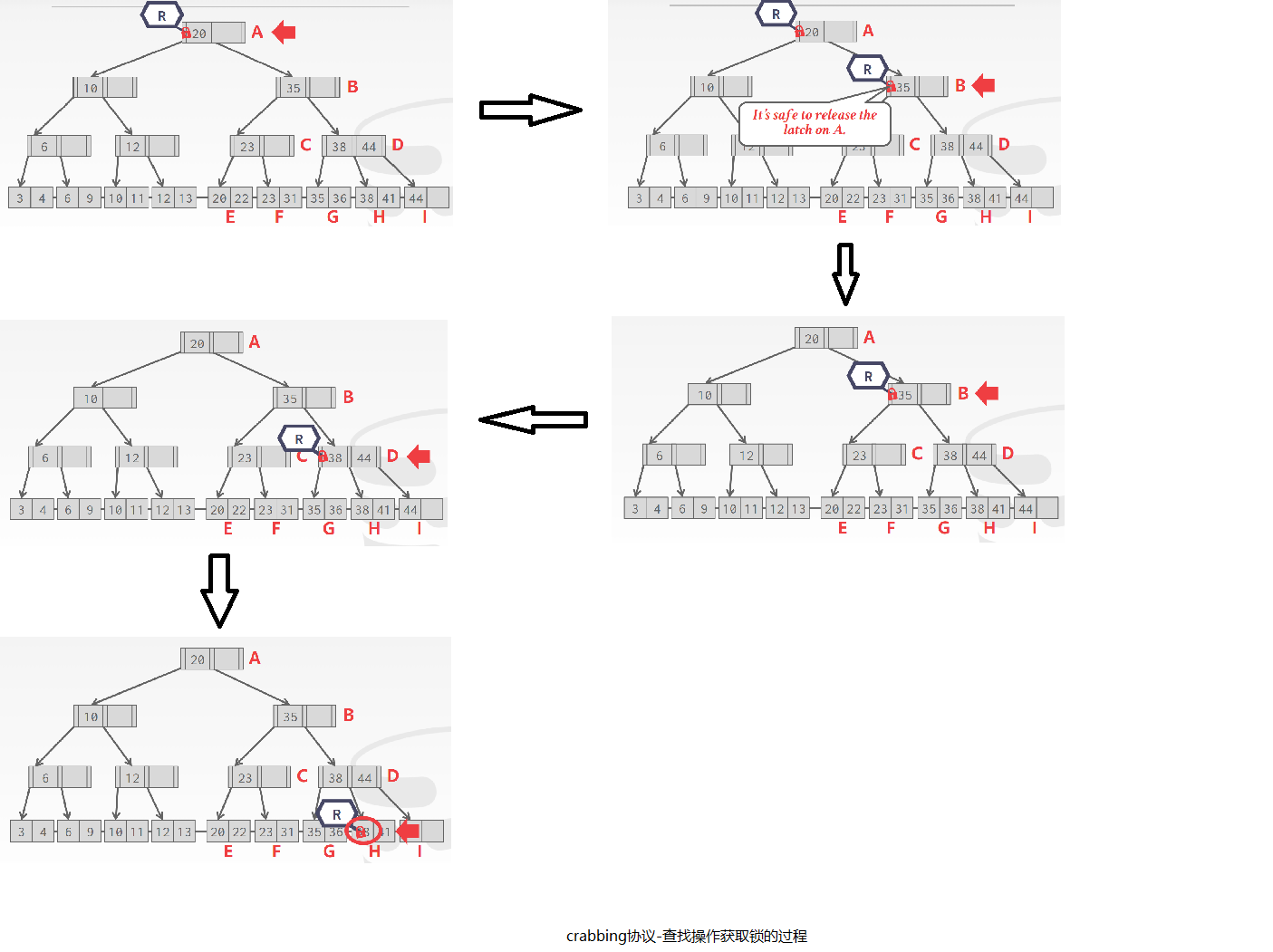
举个插入过程的例子,插入25:
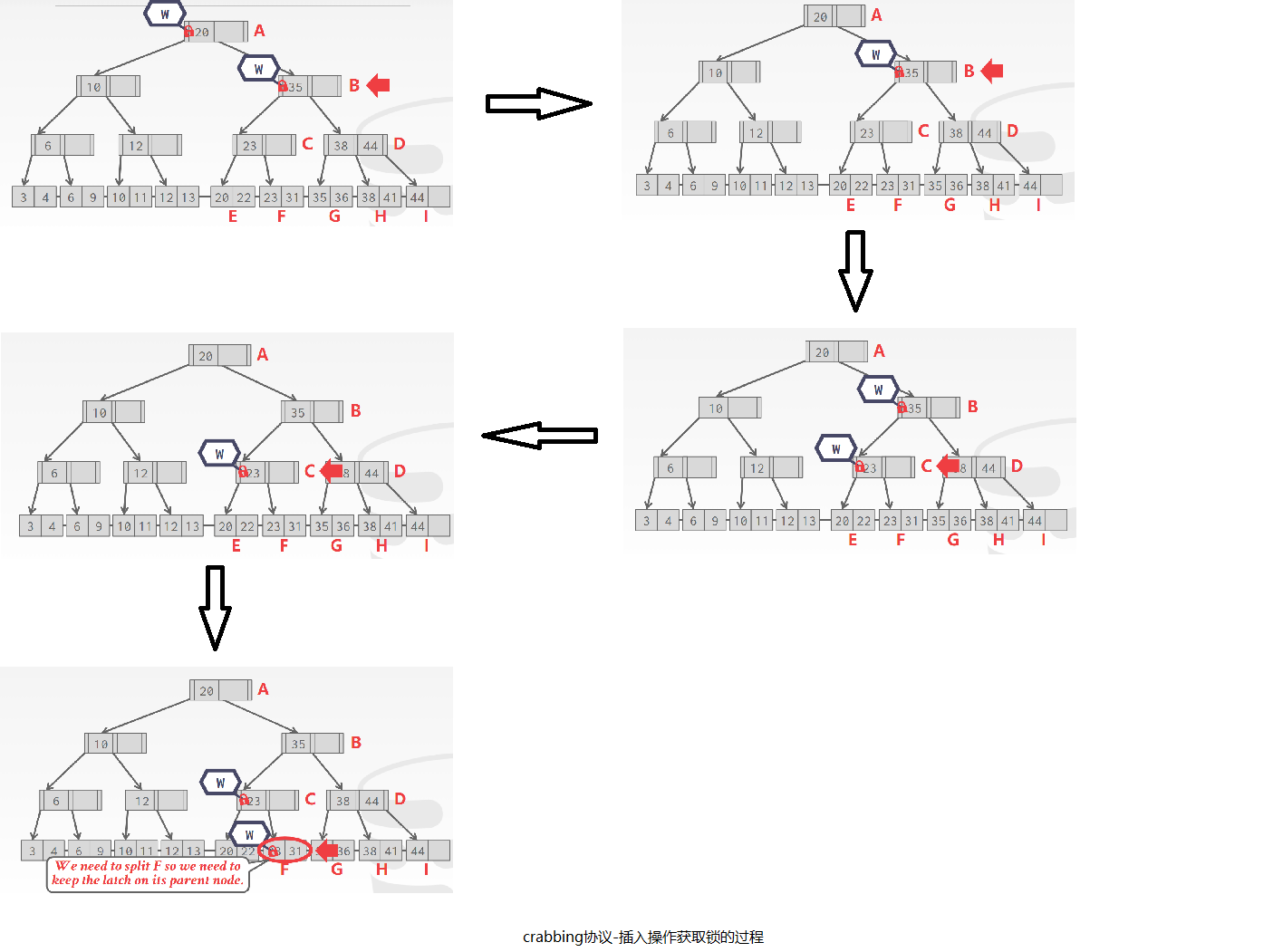
crab有螃蟹的意思,了解完crabbing协议加锁的过程,应该不难理解为什么叫crabbing协议了吧。
需要注意的地方
我们需要保护根节点id。
考虑下面这种情况:
两个线程同时执行插入操作,插入前B+树只有一个节点,线程一插入当前key后将分裂,生成一个新的根节点。另一个线程在线程一分裂前读取了旧的根节点,从而将key插入到了错误的叶子节点中。
解决办法:
在访问,修改root_page_id_的地方加锁,访问或者修改完毕root_page_id_后释放锁。root_page_id_指向的是该B+树的根节点,会保存在内存中,以便快速查找。
实验遇到的坑和解决方案
- 前文提到我们需要保护root_page_id_这个变量,可以用一个mutex,访问或修改前加锁,访问或者修改后释放锁。一次加锁只能对应一次解锁,如果多调用了一次unlock(),同样起不到保护的作用。unlock()调用分别在各个函数中,很可能不小心就多调用了次,所以千万要小心。
- 必须先释放Page上的锁,然后才能unpin该Page。为什么?我们知道unpin后,如果pin_count为0,那么这个Page将被送到LRUReplacer,当没有足够的Page时,将从LRUReplacer中取Page,将该Page的内容保存到磁盘后用于保存其它其它页的内容。考虑下面这个场景:在插入25的过程中,查找到目标叶子节点,这时该叶子节点肯定被加上了写锁,如果我们执行完插入后,先unpin了该Page,然后才释放该Page的锁。可能出现这种情况,在unpin完后,释放锁前,这个Page被送到了LRUReplacer,另一个线程请求访问页面1,但是所有的Page都被占用了,LRUReplacer选择这个淘汰带锁的这个Page来保存页面1,因为该Page的锁还没释放,所以另一个线程可以直接访问或者修改,这是回到原来的线程,再释放已经晚了。
- lab本身提供的测试case是完全不够的,就算全部通过了,也不能保证代码是正确的。我自己加入了很多测试,涵盖多个线程的,根节点分裂等case。原代码只有对BPlusTree的测试,所以我添加了对BPlusTreeInternalPage和BPlusTreeLeafPage单独的测试,这样在用BPlusTreeInternalPage和BPlusTreeLeafPage构建BPlusTree前能保证自己是正确的。
- 在使用完一个Page后应该立刻unpin掉,不能忘记unpin,如果忘记unpin的话,那么这个Page将永远不能用于保存其它页,当所有Page都被占用后,系统将无法继续运行。这个问题一度困扰我很久,一定要非常仔细。
- 本lab的一个难点是调试,多使用assert和log。




