6、Fusing IMU with complementary sensory data
将惯性测量单元与补充传感器数据融合
当接收到除IMU之外的其他信息,例如GPS或视觉信息时,对ESKF进行校正。在一个设计良好的系统中,这应该使惯性测量单元的偏差可观测,并允许ESKF正确地估计它。有许多可能性,最流行的是GPS+IMU、单目视觉+IMU、立体视觉+IMU。近年来,视觉传感器与IMU的组合引起了很多关注,因此产生了大量的科学活动。这种视觉+IMU的设置非常适用于GPS无法使用的环境,并且可以在移动设备(通常是智能手机)上实现,也可以在无人机和其他小型敏捷平台上实现。
虽然IMU信息迄今为止已经用于对ESKF进行了预测,但是其他信息用于矫正ESKF,从而观察IMU的bias误差。校正包括三个步骤:
1、通过滤波器校正误差状态的观测;
2、将观测误差注入到名义状态中;
3、误差状态重置;
6.1、通过滤波器校正误差状态的观测
假设像往常一样,我们有一个传感器,它提供取决于状态的信息,比如
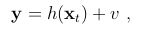
其中h()是系统状态(真实状态)的一般非线性函数,v是具有协方差V的白色高斯噪声,
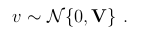
我们的滤波器正在估计误差状态,因此滤波器校正方程式也在相应地进行计算,
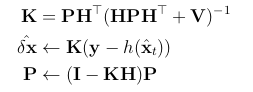
要求雅可比矩阵H的定义是相对于误差状态δx的,并在真值状态
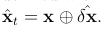 处估计.由于错误状态的均值在此阶段为零(我们尚未观察到它),因此我们有 x̂ t = x,我们可以使用名义误差 x 作为评估点,导致
处估计.由于错误状态的均值在此阶段为零(我们尚未观察到它),因此我们有 x̂ t = x,我们可以使用名义误差 x 作为评估点,导致
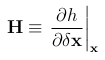
6.1.1 滤波器校正的雅可比矩阵计算
上面的雅可比矩阵可以通过多种方式计算。最具说明性的方法是利用链式法则,
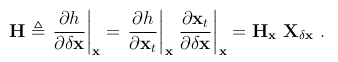
第一部分,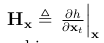 是h()相对于它自己参数的标准雅可比矩阵(例如,在常规EKF中使用的雅可比矩阵)。这个链式法则的第一部分取决于所使用的特定传感器的测量函数,本文中未进行介绍。
是h()相对于它自己参数的标准雅可比矩阵(例如,在常规EKF中使用的雅可比矩阵)。这个链式法则的第一部分取决于所使用的特定传感器的测量函数,本文中未进行介绍。
第二部分,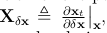 是真值状态相对于误差状态的雅可比。这部分可以在这里推导,因为它仅取决于ESKF状态的组合。有如下导数
是真值状态相对于误差状态的雅可比。这部分可以在这里推导,因为它仅取决于ESKF状态的组合。有如下导数

得到所有的3*3单位矩阵块(例如,∂(p + δp)/∂δp = I3)除了4*3的四元素项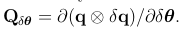 。因此有如下形式,
。因此有如下形式,
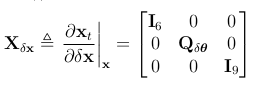
使用链式法则,极限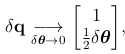 ,四元素项Qδθ可以从以下得到,
,四元素项Qδθ可以从以下得到,
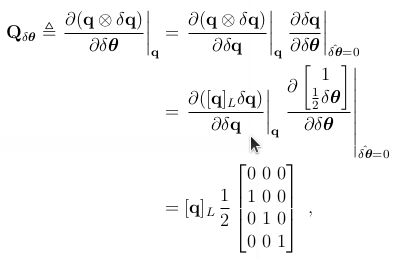
得到如下,
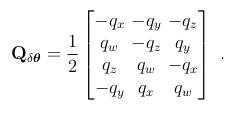
6.2 将观测误差注入到名义状态中
在ESKF更新后,使用适当的组合(求和或四元素乘积,参见表3)将观测到的误差状态与名义状态进行更新。

6.3 ESKF重置
在将误差注入到名义状态后,误差状态均值δx会被重置。与方向部分尤其相关,因为新的方向误差会局部的表达在新的名义状态的方向坐标系下。为了使ESKF更新完整,误差的协方差根据这次矫正需要更新。
称误差重置函数为g(),如下所示
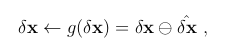
ESKF误差重置操作如下,
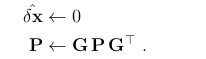
雅可比矩阵G定义如下,
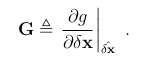
与上面更新雅可比矩阵的情况类似,这个雅可比矩阵在所有对角块上都是单位矩阵,除了方向误差。给出完整的表达式,下面是方向误差部分的导数,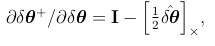
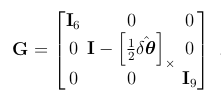
大多数情况下,误差项δθ可以被忽略,得到一个18维的单位矩阵G=I18,得到一个简单的误差重置。也是大多数ESKF实现中所做的。这里提供的表达式应该会产生更精确的结果,这可能对于减少里程计系统中的长期误差漂移是有帮助的。
6.3.1 相对于方向误差的雅可比重置操作
想要获得新的角度误差δθ+的表达式相对于老的角度误差δθ以及观测误差δθ^,考虑如下事实:
真方向不会因误差项重置而改变,例如,qt+ = qt .如下:
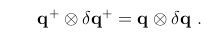
观测误差均值注入到名义状态:
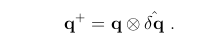
δq+表达式如下,
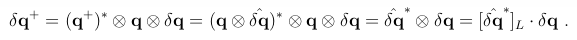
由于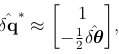 ,对上面式子进行展开,
,对上面式子进行展开,
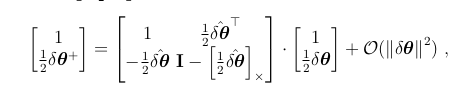
给出一个标量和一个向量方程,
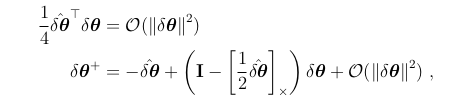
第一个问题并不是非常具有信息量,因为它只涉及到无穷小的关系。从第二个方程式可以证明,δθ+=0,与我们对重置操作的期望相符。通过简单的推导,可以得到雅可比矩阵,
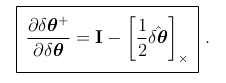


 浙公网安备 33010602011771号
浙公网安备 33010602011771号