IMU学习

参考https://zhuanlan.zhihu.com/p/356693537

IMU在定位、建图等系统中都是非常核心的传感器。

使用IMU时，核心问题是建立IMU测量值z与系统状态之间的关系 。建立这种关系可以采用两种形式：

1）积分

2）微分

还有一个有趣的现象，迭代形式的IMU预积分公式与直接积分公式，在重力为0的情况下，是相同的。

这样在写代码时我们可以只实现直接积分方法，把重力设成0就变成了预积分了。

1、积分形式的用法

这种方式通过积分IMU数据的形式，建立IMU与State的关系

1.1 IMU ODE

 

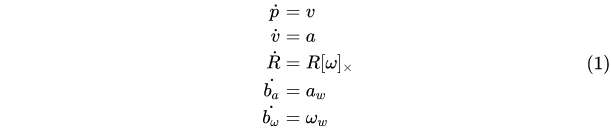
 具体可参考:https://arxiv.org/abs/1711.02508

1.2在滤波算法中的用法

滤波算法中，如EKF，一般用IMU做状态预测。相关的系统如IMU&GPS惯导，MSCKF等。具体的就是对（1）式进行积分，将k时刻的state predict到k+1时刻。

 

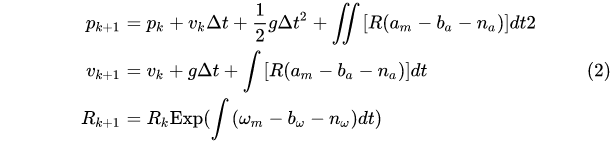
 对于上面的式子可以采用各种数值积分（欧拉、中值、RK4）计算。以Euler积分为例：

 

 采用这个式子，就可以做EKF的预测了。状态转移矩阵/雅克比的具体形式可参考这里：https://docs.openvins.com/propagation.html

1.3在优化算法中的用法

IMU的频率远高于相机/Lidar的帧率，基于优化的系统，如VIO/LIO中，一般将两个（关键）帧之间的IMU做积分，形成与两端state的关系方程。构造这个方程有两种方法。

1.3.1直接积分法

 采用（2）式，对IMU进行直接积分，从上一个关键帧state推演到下一个关键帧。这样，我们可以建立下面的约束。

 

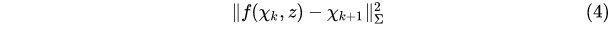
这种方法的缺点很明显，每次优化迭代之后， 变化，积分就要重新计算。

但是优势也很突出，每次都重新积分，意味着更高的精度。如果对精度要求高，又不在意计算量，建议采用这种形式。

1.3.2 预积分

预积分开始由Lupton提出，后来由Forster推广到了manifold上面。李明扬在MSCKF2.0中也有提到相关的思想。最关键的Paper是https://ieeexplore.ieee.org/document/7557075

（4）式的问题是不能把约束建立成，z为常量，这种形式。这种形式的方程，当状态变化时，也不会影响到z。预积分的精髓就在于，找到一个与状态无关的测量值z。

具体的，我们把（2）式重写一下，将积分基准设在k帧上， 就与状态无关了，就是我们的预积分量。

 

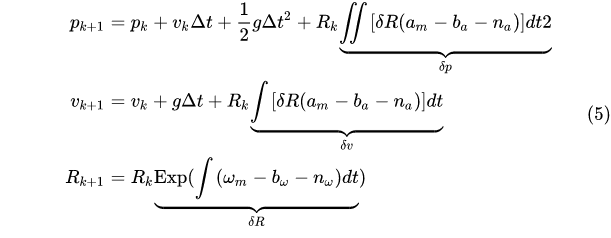
 预积分的迭代形式为：

 

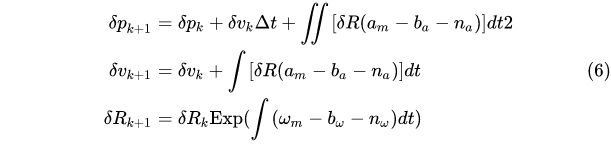
 我们对比一下（6）式和（2）式可以发现一个很有意思的现象：把（2）式中的重力加速度 设置成0，（2）和（6）两者在形式上是完全相同的。就是说，迭代形式的IMU预积分公式与IMU直接积分相同。这样我们在写代码的时候，只需要写个直接积分的代码。把重力设成0就可以直接当预积分去使用。

上面的与积分假设了IMU bias不变，但是实际优化过程中 IMU bias是会变的。因此需要进行补偿。具体的是采用一阶近似。

这种近似相对于直接积分的方法就有一些精度损失。

预积分的好处是可以避免重复积分。
但是因为有一些近似，比如（7）式，所以理论上精度上不如直接积分。

具体的预积分实现和论文请可以参考：

https://github.com/borglab/gtsam/tree/develop/gtsam/navigation

https://github.com/UZ-SLAMLab/ORB_SLAM3/blob/master/src/ImuTypes.cc

https://github.com/HKUST-Aerial-Robotics/VINS-Mono/blob/master/vins_estimator/src/factor/integration_base.h

2、微分形式的用法

我们如果对IMU数据进行积分，就可以得到pose，从而可以建立IMU与state的关系。那么我们反过来想，对state进行微分，一阶微分就可以得到速度、角速度，二阶微分就可以得到加速度，这样也可以建立IMU的角速度、加速度与state的关系。

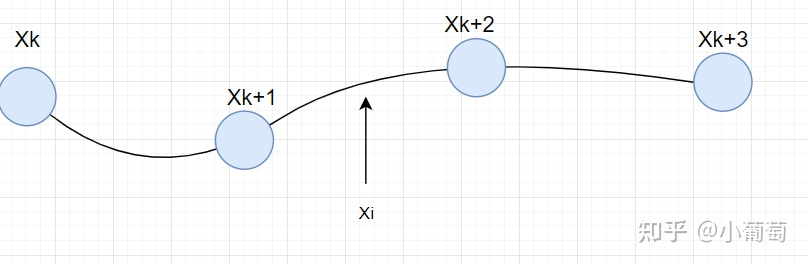
关键是如何对state进行微分呢？而且state一般是离散分布的。常用的办法是插值，给定一些离散的state，可以通过插值获取任意时刻的pose。比较常用的插值方法是b-spline。如下图，我们可以在一个IMU采样时刻，插值一个state ，由与其相邻的四个state插值而来。

 

 

 

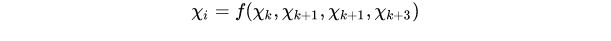
 对其进行相对时间的微分，可以建立与IMU的关系，即加速度的误差和角速度的误差。

 

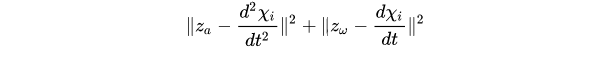
 具体形式，可参考：

https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=8432102

https://vision.cs.tum.edu/_media/spezial/bib/sommer19spline.pdf