METHODS FOR NON-LINEAR LEAST SQUARES PROBLEMS-2.3 线性搜索-2.4信任区域

2.3 线性搜索

给定一个点x以及下降方向h。下一个迭代步从x沿着h的方向移动。为了找出，移动了多远，本文研究给定方程沿着half line（中线的意思？？）从x方向为h，

 φ(α)的一个行为例子如下图所示：

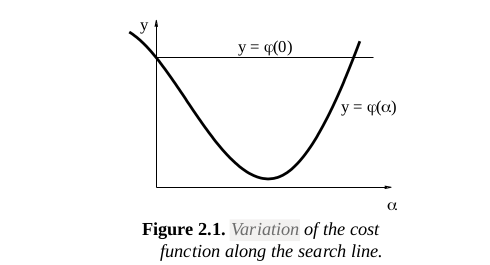
h作为下降的方向保证了（前提是h作为下降方向），上图中F’（x）的导数小于0，在a=0处；

 如果a充分小，表明满足下降条件(2.1),等价于

                                           φ(α) < φ(0)

通常，我们给出一个a的初始猜测，例如a=1用牛顿方法，上图证明了三个不同的情形出现

1、α is so small that the gain in value of the objective function is verysmall. α should be increased.

2、α is too large: φ(α) ≥ φ(0). Decrease α in order to satisfy the descent condition (2.1).

3、α is close to the minimizer 1) of φ(α). Accept this α-value.

一个精确的线性搜索是一个迭代的过程产生一系列a1，a2，....。目标是找到真正的最小a_e在（2.7)中定义，当迭代a_s满足如下，则停止

 

没明白上面的！！！！！？？？？

2.4Trust Region and Damped Methods

假设有一个模型L，这个模型是F在当前迭代x的附近的行为，如下

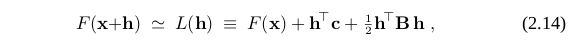
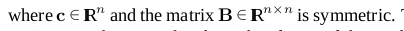 这部分的基本意思可能归纳为模型的其他形式，但是在本册子里面我们只讨论（2.14）中给出的L形式。通常，这个模型是F在x周围的一个二阶泰勒展开式，L(h)可能是这个展开的一个近似。通常认为当h足够小的时候，这是一个好的模型。我们将介绍两个方法来决定步长h，h是下降的方向。

在信任区域方法中，我们认为我们知道一个正数δ，以便这个模型以δ为半径的一个球体内这个模型是充分精确的，球体的中心在x，步长的决定如下：

 在阻尼方法中，步长定义如下：

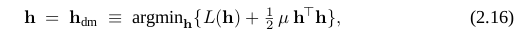
 上面阻尼参数μ大于等于0.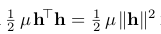阻尼项被认为是惩罚大的步长的情况。

算法2.4的核心部分是基于上面两个方法之一，形式如下：

如果步长h满足式（2.1）的下降条件，对应于a=1，否则，a=0，例如不移动。但是，不能在x处卡住（除非x = x*）:通过适当调整δ或者μ，旨在在下一步迭代中获得更好的结果。

因为L（h）被认为是当h很小的时候，是对F（x+h）的一个好的近似，出现步长失败的原因是因为h太大了，应该被减小。进一步，如果步长被接受，这有可能在新一轮迭代时使用更大的步长，因此可以减少到达x*所需要的步长数量。

在计算的步长下，模型的质量可以通过所谓的增益率来评价

 例如这个比率是函数的实际值之差与预测值之差的比率。

 按照以上结构分母是正的，分子是负的如果这个步长不是下降的话----这太大了，应该被减小。

用信任区域的方法，我们通过半径δ的大小来监控步长。下面的更新策略被广泛使用：

 因此，如果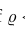<1/4,我们决定用更小的步长，当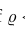大于3/4表明有可能使用更大的步长。一个信任区域算法在阈值1/4和3/4之间值的变化不会敏感，除数p1=2或者倍数p2=3，p1和p2的选择很重要以便δ值不会震荡。

在阻尼方法中一个小的值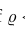表明我们应该增加阻尼因子，因此对大的步长增加惩罚项。一个大的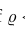值表明L(h)是对F（x+h）一个好的近似，阻尼应该被减小。一个被广泛应用的策略如下，类似于(2.19)

 同样的，在阈值0.25与0.75之间的小的变化，本方法不会敏感，或者p1=2，p2=3也不会敏感，但是p1和p2的选择很重要以便μ值不会震荡。经验表明在阈值0.25和0.75之间的不连续的改变可能会引起“颤震”，这会减慢收敛，以下策略更常用：

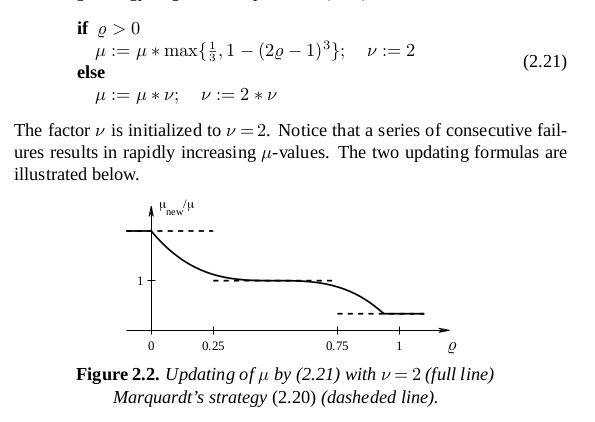
 2.4.1 步长的计算。

 在阻尼算法中，这一步作为函数的驻点来计算

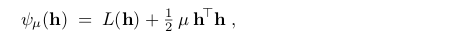
 这就意味着h_dm是下面的解答

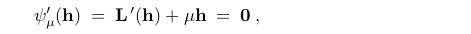
 从（2.14）中L(h)的定义我们可以知道是等同于如下的

 I是单位矩阵，如果μ充分大，对称矩阵B+μI是正定的，则其服从定理1.8，h_dm是L的最小取值部分。

例子2.1 在阻尼牛顿算法中，模型L（h）由c=F’（x）以及B=F‘’（x）给定，以及（2.22），形式如下：

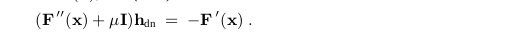
 h_dn称为阻尼牛顿步，如果μ是非常大，那么

 例如在接近最速下降法的方向上的一个小的步长，另一方面，如果μ很小，那么h_dn是接近于牛顿步h_n。因此，我们认为阻尼牛顿方法作为最速下降法和牛顿法的一个混合方法。

在3.2节中我们回到阻尼方法

在一个信任区域方法中步长h_tr是对一个约束优化问题的解答，

 如果在（2.14）中矩阵B是正定的，那么L的无约束最小问题的解如下：

 如果这是充分小的（满足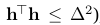），这是期望的步长h_tr。否则，约束是激活的，问题就更加复杂。

最后，我们提出在阻尼方法和信任区域方法之间的两个相似性假设B是正定的：在无约束中，最小值是在信任区域外，证明存在一个λ>0以便有

 通过对方程重新排序，将它与（2.22）相比较，得出h_tr与阻尼步长h_dm（阻尼参数μ=λ）是一致的。另一方面，也可以证明如果在给定μ大于等于0，我们计算h_dm，有

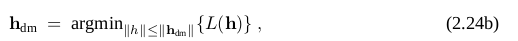
 例如h_dm与h_tr相等对应于信任区域半径δ=||h_dm||。因此，这两类方法是相关的，但是没有一个简单的方程可以把他们在δ和μ值在给出相同的步基础上联系起来。