[原创]桓泽学音频编解码(14):AC3 时频转换模块算法分析
[原创]桓泽学音频编解码(1):MPEG1 MP3 系统算法分析
[原创]桓泽学音频编解码(2):AC3/Dolby Digital 系统算法分析
[原创]桓泽学音频编解码(4):MP3 和 AAC 中反量化原理,优化设计与参考代码中实现
[原创]桓泽学音频编解码(5):MP3 和 AAC 中IMDCT算法的原理,优化设计与参考代码中实现
[原创]桓泽学音频编解码(6):MP3 无损解码模块算法分析
[原创]桓泽学音频编解码(7):MP3 和 AAC 中huffman解码原理,优化设计与参考代码中实现
[原创]桓泽学音频编解码(8):关于MP3和AAC量化器设计的研究
[原创]桓泽学音频编解码(9):MP3 多相滤波器组算法分析
[原创]桓泽学音频编解码(12):AC3 Mantissa(小数部分)模块算法分析
1 时频转换算法概述
AC-3 采用了MDCT来把时间域上的讯号样本转换到频率域上。MDCT是TDAC(time domain aliasing cancellation) filter的一种实现,可以由频率域上的讯号完美地重建成原来空间域上的讯号,且其输入的 PCM 讯号事先会经过一个变换窗序列,标准中直接给出了窗系数的表,而长度则由块选择模型来决定为512或256点。
α = –1 用于第一个短块变换
0 用于长块变换
+1 用于第二个短块变换
x[n]是作了窗处理的时域系数
N=512 或 256
进入变换之前,先使用标准中给出的窗系数对512个PCM数据加窗。然后,在进行长块变换时,整个512个数据统一进行,产生256个频域系数。当进行短块变换时,512个采样要分成2个部分,前一半和后一般分开进行变换。每个半块变换操作后产生128个频域系数,再把2个半块的数据交织到一起构成一个具有256个频域系数的块。这个块的量化和发送与长块一致。
每个块的标志会通过blksw[ch]标志传送给解码器,解码器根据这个标志去对短块数据进行解交织。
2 AC3 时频转换算法原理
AC3的TDAC反变换要经过3个处理过程,第一步是IMDCT处理使频域数据变成时域数据。第二步是加窗。第三步是交叠相加过程。这个部分的输入输出如下
输入:blksw[i]:标记块是长块还是短块。‘0’是长块,‘1’是短块。频域信号 32位浮点
输出:时域信号 32位浮点
2.1 IMDCT
IMDCT的公式如下
Xk 是输入频域数据。Xi是输出时域数据
⑴ AC3 长块的反变换 N=512
⑵ AC3 第一个短块的反变换 N=256
⑶ AC3 第二个短块的反变换 N=256

2.2 加窗
AC3标准中使用KBD窗对时域系数进行加窗处理。窗系数如标准中相关表格。
2.3 交叠相加
与AAC和mp3标准类似。AC3的交叠相加处理也是将加窗块的前一半和上一块的后一半互相重叠产生PCM样本。其中输入512个数据,输出256个PCM样本。如图
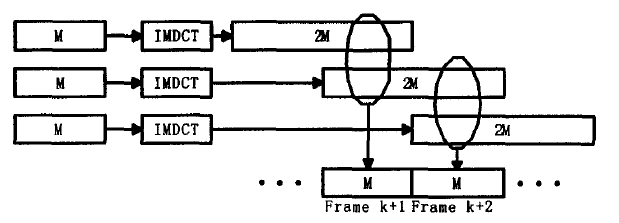
M=256
3 优化算法
对时频反变换的算法,AC3在标准中直接给出了快速算法(radix-4的FFT算法),过程如下。
3.1 长块执行步骤
Step1
定义变换系数 X[k], k = 0, 1,...N/2–1.
Step2 Pre-IFFT 复数乘部分
计算N/4点的复数乘,Z[k], k = 0, 1,...N/4–1:
for(k=0; k<N/4; k++)
{
/* Z[k] = (X[N/2-2*k-1] + j * X[2*k]) * (xcos1[k] + j * xsin1[k]) ; */
Z[k]=(X[N/2-2*k-1]*xcos1[k]-X[2*k]*xsin1[k])+j*(X[2*k]*xcos1[k]+X[N/2-2*k-1]*xsin1[k]);
}
在这里
xcos1[k] = –cos (2 p * (8 * k + 1)/(8 * N))
xsin1[k] = –sin (2 p * (8 * k + 1)/(8 * N))
Step3: IFFT
for(n=0; n<N/4; n++)
{
z[n] = 0 ;
for(k=0; k<N/4; k++)
{
z[n] + = Z[k] * (cos(8*π*k*n/N) + j * sin(8*π*k*n/N)) ;
}
}
Step4:Post-IFFT复数乘
计算N/4点复数乘,产生y(n), n = 0, 1,...N/4–1
for(n=0; n<N/4; n++)
{
/* y[n] = z[n] * (xcos1[n] + j * xsin1[n]) ; */
y[n] = (zr[n] * xcos1[n] - zi[n] * xsin1[n]) + j * (zi[n] * xcos1[n] + zr[n] * xsin1[n]) ;
}
zr[n] = real(z[n])
zi[n] = imag(z[n])
xcos1[n] = –cos (2 p * (8 * n + 1)/(8 * N))
xsin1[n] = –sin (2 p * (8 * n + 1)/(8 * N))
Step5:加窗和去交织
计算时域信号x[n]:
for(n=0; n<N/8; n++)
{
x[2*n] = -yi[N/8+n] * w[2*n] ;
x[2*n+1] = yr[N/8-n-1] * w[2*n+1] ;
x[N/4+2*n] = -yr[n] * w[N/4+2*n] ;
x[N/4+2*n+1] = yi[N/4-n-1] * w[N/4+2*n+1] ;
x[N/2+2*n] = -yr[N/8+n] * w[N/2-2*n-1] ;
x[N/2+2*n+1] = yi[N/8-n-1] * w[N/2-2*n-2] ;
x[3*N/4+2*n] = yi[n] * w[N/4-2*n-1] ;
x[3*N/4+2*n+1] = -yr[N/4-n-1] * w[N/4-2*n-2] ;
}
yr[n] = real(y[n])
yi[n] = imag(y[n])
w[n] 是窗系数,见AC3表7.33
Step6 交叠加
for(n=0; n<N/2; n++)
{
pcm[n] = 2 * (x[n] + delay[n]) ;
delay[n] = x[N/2+n) ;
}
3.2 短块执行步骤
Step1
定义变换系数 X[k], k = 0, 1,...N/2–1.
for(k=0; k<N/4; k++)
{
X1[k] = X[2*k] ;
X2[k] = X[2*k+1] ;
}
Step2
N/8-point 复数乘产生Z1(k) 和 Z2(k), k = 0, 1,...N/8–1.
for(k=0; k<N/8; k++)
{
/* Z1[k] = (X1[N/4-2*k-1] + j * X1[2*k]) * (xcos2[k] + j * xsin2[k]); */
Z1[k]=(X1[N/4-2*k-1]*xcos2[k]-X1[2k]*xsin2[k])+j*(X1[2*k]*xcos2[k]+X1[N/4-2*k-1]*xsin2[k]) ;
/* Z2[k] = (X2[N/4-2*k-1] + j * X2[2*k]) * (xcos2[k] + j * xsin2[k]) ; */
Z2[k]=(X2[N/4-2*k-1]*xcos2[k]-X2[2*k]*xsin2[k])+j*(X2[2*k]*xcos2[k]+X2[N/4-2*k-1]*xsin2[k]) ;
}
在这里
xcos2[k] = -cos(2p*(8*k+1)/(4*N)), xsin2(k) = -sin(2p*(8*k+1)/(4*N))
Step3
计算N/8点的IFFT得到复数值序列z1[n],z2[n]
for(n=0; n<N/8; n++)
{
z1[n] = 0. ;
z2[n] = 0. ;
for(k=0; k<N/8; k++)
{
z1[n] + = Z1[k] * (cos(16*π*k*n/N) + j * sin(16*π*k*n/N)) ;
z2[n] + = Z2[k] * (cos(16*π*k*n/N) + j * sin(16*π*k*n/N)) ;
}
}
Step4
计算N/8点的复数乘产生y1[n] and y2[n], n = 0, 1,...N/8–1.
for(n=0; n<N/8; n++)
{
/* y1[n] = z1[n] * (xcos2[n] + j * xsin2[n]) ; */
y1[n] = (zr1[n] * xcos2[n] - zi1[n] * xsin2[n]) + j * (zi1[n] * xcos2[n] + zr1[n] * xsin2[n]) ;
/* y2[n] = z2[n] * (xcos2[n] + j * xsin2[n]) ; */
y2[n] = (zr2[n] * xcos2[n] - zi2[n] * xsin2[n]) + j * (zi2[n] * xcos2[n] + zr2[n] * xsin2[n]) ;
}
Step5
计算加窗的时域信号x[n].
for(n=0; n<N/8; n++)
{
x[2*n] = -yi1[n] * w[2*n] ;
x[2*n+1] = yr1[N/8-n-1] * w[2*n+1] ;
x[N/4+2*n] = -yr1[n] * w[N/4+2*n] ;
x[N/4+2*n+1] = yi1[N/8-n-1] * w[N/4+2*n+1] ;
x[N/2+2*n] = -yr2[n] * w[N/2-2*n-1] ;
x[N/2+2*n+1] = yi2[N/8-n-1] * w[N/2-2*n-2] ;
x[3N/4+2*n] = yi2[n] * w[N/4-2*n-1] ;
x[3N/4+2*n+1] = -yr2[N/8-n-1] * w[N/4-2*n-2] ;
}
其中
yr1[n] = real(y1[n])
yi1[n] = imag(y1[n])
yr2[n] = real(y2[n])
yi2[n] = imag(y2[n])
w[n]是窗函数
Step6 交叠加
当前块的前半部分数据和前一个块的后半部分数据相加
for(n=0; n<N/2; n++)
{
pcm[n] = 2 * (x[n] + delay[n]) ;
delay[n] = x[N/2+n] ;
}
4 参考代码
AC3的参考代码部分实现方法与快速算法的伪代码几乎完全一致。故略去。


