逆向中的常见密码的识别(持续更新中)
最近半年打了很多比赛,也见了很多的逆向方向的题目。对于解决对比密文类的逆向题,往往绕不开的一个问题就是对于加密算法的识别。
下面就分类对于各种加密的特征以及识别方法进行总结。
流密码
常见的有 RC4、Salsa20 以及 ChaCha20。但是识别出是指定加密是何种流密码其实并不是非常的重要,一般情况下只要识别出来是流密码就可以了,特征就是密文仅由明文与密钥流经过异或运算得到。只要识别出流密码,我们就可以选择动态调试获取密钥流或者直接把目标密文 patch 进去拿输出就可以了。
RC4
/*初始化函数*/ void rc4_init(unsigned char *s, unsigned char *key, unsigned long Len) { int i = 0, j = 0; char k[256] = {0}; unsigned char tmp = 0; for (i = 0; i < 256; i++) { s[i] = i; k[i] = key[i % Len]; } for (i = 0; i < 256; i++) { j = (j + s[i] + k[i]) % 256; tmp = s[i]; s[i] = s[j]; // 交换s[i]和s[j] s[j] = tmp; } } /*加解密*/ void rc4_crypt(unsigned char *s, unsigned char *Data, unsigned long Len) { int i = 0, j = 0, t = 0; unsigned long k = 0; unsigned char tmp; for (k = 0; k < Len; k++) { i = (i + 1) % 256; j = (j + s[i]) % 256; tmp = s[i]; s[i] = s[j]; // 交换s[x]和s[y] s[j] = tmp; t = (s[i] + s[j]) % 256; Data[k] ^= s[t]; } }
RC4 实现非常简单,特征也非常明显:
长度为 256 的 S 盒,且在每一步生成与加密过程中都伴随着 S 盒的 swap
Salsa20
Salsa20算法通过将 32 字节(或者 16 字节)的密钥 和 **8 字节的iv **扩展为伪随机密钥字节流,通过伪随机密钥字节流和异或操作实现加解密。
伪随机密钥字节流的生成
伪随机密钥字节流的生成其实是使用 密钥、iv、以及一些常量构成 64 字节数据,输入到核心函数中得到 64 字节的输出。
Salsa20 密钥拓展规则如下:
# key 为 32 字节时 c[0] + key[0:16] + c[1] + iv + 计数器(8 bytes) + key[16:32] + c[4] c = [0x61707865, 0x3320646e, 0x79622d32, 0x6b206574] # expand 32-byte k # key 为 16 字节时 c[0] + key[0:16] + c[1] + iv + 计数器(8 bytes) + key[0:16] + c[4] c = [0x61707865, 0x3120646e, 0x79622d36, 0x6b206574] # expand 16-byte k
** 核心函数实现: **
#define R(a,b) (((a) << (b)) | ((a) >> (32 - (b)))) void salsa20_word_specification(uint32 out[16],uint32 in[16]) { int i; uint32 x[16]; for (i = 0; i < 16; ++i) x[i] = in[i]; for (i = 20; i > 0; i -= 2) { // 迭代次数,注意每次 i -= 2 ! // 每列 x[ 4] ^= R(x[ 0]+x[12], 7); x[ 8] ^= R(x[ 4]+x[ 0], 9); x[12] ^= R(x[ 8]+x[ 4],13); x[ 0] ^= R(x[12]+x[ 8],18); x[ 9] ^= R(x[ 5]+x[ 1], 7); x[13] ^= R(x[ 9]+x[ 5], 9); x[ 1] ^= R(x[13]+x[ 9],13); x[ 5] ^= R(x[ 1]+x[13],18); x[14] ^= R(x[10]+x[ 6], 7); x[ 2] ^= R(x[14]+x[10], 9); x[ 6] ^= R(x[ 2]+x[14],13); x[10] ^= R(x[ 6]+x[ 2],18); x[ 3] ^= R(x[15]+x[11], 7); x[ 7] ^= R(x[ 3]+x[15], 9); x[11] ^= R(x[ 7]+x[ 3],13); x[15] ^= R(x[11]+x[ 7],18); // 每行 x[ 1] ^= R(x[ 0]+x[ 3], 7); x[ 2] ^= R(x[ 1]+x[ 0], 9); x[ 3] ^= R(x[ 2]+x[ 1],13); x[ 0] ^= R(x[ 3]+x[ 2],18); x[ 6] ^= R(x[ 5]+x[ 4], 7); x[ 7] ^= R(x[ 6]+x[ 5], 9); x[ 4] ^= R(x[ 7]+x[ 6],13); x[ 5] ^= R(x[ 4]+x[ 7],18); x[11] ^= R(x[10]+x[ 9], 7); x[ 8] ^= R(x[11]+x[10], 9); x[ 9] ^= R(x[ 8]+x[11],13); x[10] ^= R(x[ 9]+x[ 8],18); x[12] ^= R(x[15]+x[14], 7); x[13] ^= R(x[12]+x[15], 9); x[14] ^= R(x[13]+x[12],13); x[15] ^= R(x[14]+x[13],18); } for (i = 0;i < 16;++i) out[i] = x[i] + in[i]; }
后面接着就是 xor 了,看了前面的实现代码,我相信这种加密的识别也并不困难
首先,构造核心函数输入时的参数,是最容易识别的。(当然也是最容易魔改的)
其次,核心函数中的标志性循环左移,以及每一位对应的位移数,不要看着复杂,其实就是 7、9、13、18,可以看到上面的代码中我把每4个分成了一组,因为在实现的时候有时候会把每四个作为一组来处理。
#define quarter(a,b,c,d) do {\ b ^= R(d+a, 7);\ c ^= R(a+b, 9);\ d ^= R(b+c, 13);\ a ^= R(c+d, 18);\ } while (0) void salsa20_words(uint32_t *out, uint32_t in[16]) { uint32_t x[4][4]; int i; for (i=0; i<16; ++i) x[i/4][i%4] = in[i]; for (i=0; i<10; ++i) { // 10 double rounds = 20 rounds // column round: quarter round on each column; start at ith element and wrap quarter(x[0][0], x[1][0], x[2][0], x[3][0]); quarter(x[1][1], x[2][1], x[3][1], x[0][1]); quarter(x[2][2], x[3][2], x[0][2], x[1][2]); quarter(x[3][3], x[0][3], x[1][3], x[2][3]); // row round: quarter round on each row; start at ith element and wrap around quarter(x[0][0], x[0][1], x[0][2], x[0][3]); quarter(x[1][1], x[1][2], x[1][3], x[1][0]); quarter(x[2][2], x[2][3], x[2][0], x[2][1]); quarter(x[3][3], x[3][0], x[3][1], x[3][2]); } for (i=0; i<16; ++i) out[i] = x[i/4][i%4] + in[i]; }
最后提醒下,Salsa20 核心函数中的 20 轮也是可以魔改的。
ChaCha20
ChaCha20 加密基本上和 Salsa20差不多,作者也是同一个人。ChaCha20 的 密钥为 32 字节,iv 为 12 字节, 计数器为 4 字节
伪随机密钥字节流的生成
ChaCha20 密钥拓展规则如下:
c[0:4] + key[0:32] + 计数器(4 bytes) + iv c = [0x61707865, 0x3320646e, 0x79622d32, 0x6b206574] # expand 32-byte k
核心函数的实现:
static inline void u32t8le(uint32_t v, uint8_t p[4]) { p[0] = v & 0xff; p[1] = (v >> 8) & 0xff; p[2] = (v >> 16) & 0xff; p[3] = (v >> 24) & 0xff; } static inline uint32_t u8t32le(uint8_t p[4]) { uint32_t value = p[3]; value = (value << 8) | p[2]; value = (value << 8) | p[1]; value = (value << 8) | p[0]; return value; } static inline uint32_t rotl32(uint32_t x, int n) { // http://blog.regehr.org/archives/1063 return x << n | (x >> (-n & 31)); } // https://tools.ietf.org/html/rfc7539#section-2.1 static void chacha20_quarterround(uint32_t *x, int a, int b, int c, int d) { x[a] += x[b]; x[d] = rotl32(x[d] ^ x[a], 16); x[c] += x[d]; x[b] = rotl32(x[b] ^ x[c], 12); x[a] += x[b]; x[d] = rotl32(x[d] ^ x[a], 8); x[c] += x[d]; x[b] = rotl32(x[b] ^ x[c], 7); } static void chacha20_serialize(uint32_t in[16], uint8_t output[64]) { int i; for (i = 0; i < 16; i++) { u32t8le(in[i], output + (i << 2)); } } static void chacha20_block(uint32_t in[16], uint8_t out[64], int num_rounds) { int i; uint32_t x[16]; memcpy(x, in, sizeof(uint32_t) * 16); for (i = num_rounds; i > 0; i -= 2) { chacha20_quarterround(x, 0, 4, 8, 12); chacha20_quarterround(x, 1, 5, 9, 13); chacha20_quarterround(x, 2, 6, 10, 14); chacha20_quarterround(x, 3, 7, 11, 15); chacha20_quarterround(x, 0, 5, 10, 15); chacha20_quarterround(x, 1, 6, 11, 12); chacha20_quarterround(x, 2, 7, 8, 13); chacha20_quarterround(x, 3, 4, 9, 14); } for (i = 0; i < 16; i++) { x[i] += in[i]; } chacha20_serialize(x, out); }
和 Salsa20 整体来说基本一致,识别方法也基本一样,对于二者的区别主要是:
密钥拓展规则的不同
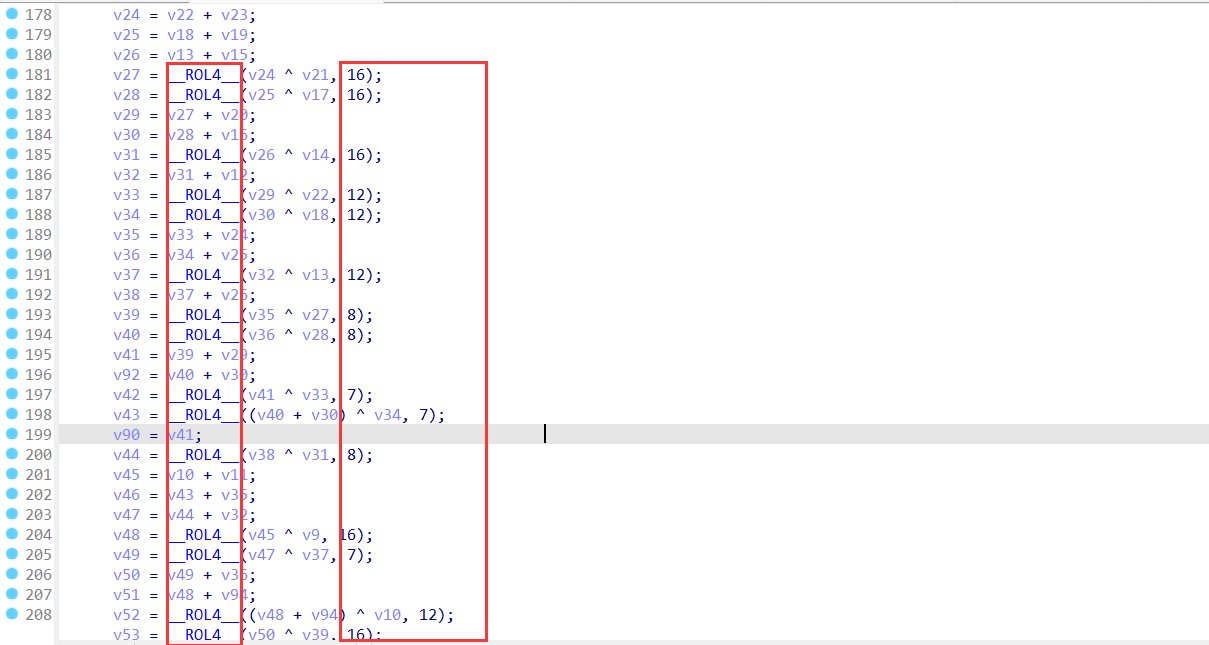
quarterround 也不同,其中做容易看出来的就是 ChaCha20 的移位为 16 12 8 7,其他的就要看具体的运算逻辑了
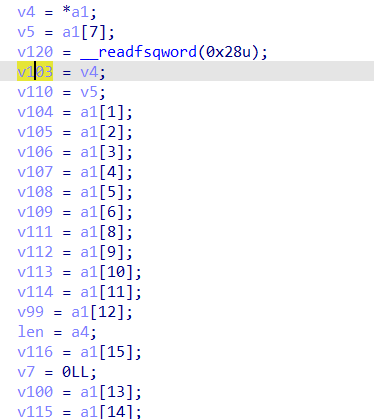
比如最近 RCTF2022 中的checkserver 中的加密,
单看密钥 64 字节,没有iv,也没有常量,看起来好像不是 ChaCha20,但是看后面,标志性的循环左移16 12 8 7,我们就可以很容易的识别出来,这是一个去除了密钥拓展的 ChaCha20.
分组密码
TEA
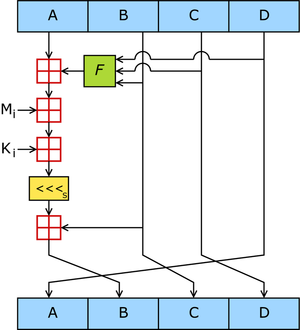
微型加密算法(Tiny Encryption Algorithm,TEA)是一种易于描述和执行的分组密码,密钥长度为128位,分组长度为 64 位,基于 Feistel 结构,流程图如下:
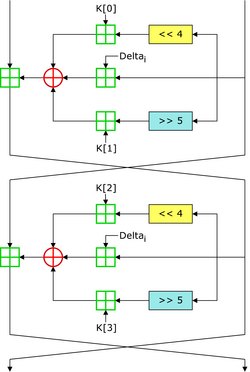
下面是 TEA 的实现
#include <stdint.h> void encrypt (uint32_t* v, uint32_t* k) { uint32_t v0=v[0], v1=v[1], sum=0, i; /* set up */ uint32_t delta=0x9e3779b9; /* a key schedule constant */ uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */ for (i=0; i < 32; i++) { /* basic cycle start */ sum += delta; v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1); v1 += ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3); } /* end cycle */ v[0]=v0; v[1]=v1; } void decrypt (uint32_t* v, uint32_t* k) { uint32_t v0=v[0], v1=v[1], sum=0xC6EF3720, i; /* set up */ uint32_t delta=0x9e3779b9; /* a key schedule constant */ uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */ for (i=0; i<32; i++) { /* basic cycle start */ v1 -= ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3); v0 -= ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1); sum -= delta; } /* end cycle */ v[0]=v0; v[1]=v1; }
可以看出,TEA 的实现确实非常简单,对于TEA的识别,特征常量 delta 0x9e3779b9 是一个非常重要的特征,但是delta在赛题中往往会被魔改为其他数值,这种情况下就需要通过对 Feistel 结构的识别和移位操作的识别来识别了。
XTEA
#include <stdint.h> /* take 64 bits of data in v[0] and v[1] and 128 bits of key[0] - key[3] */ void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) { unsigned int i; uint32_t v0=v[0], v1=v[1], sum=0, delta=0x9E3779B9; for (i=0; i < num_rounds; i++) { v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]); sum += delta; v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]); } v[0]=v0; v[1]=v1; } void decipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) { unsigned int i; uint32_t v0=v[0], v1=v[1], delta=0x9E3779B9, sum=delta*num_rounds; for (i=0; i < num_rounds; i++) { v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]); sum -= delta; v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]); } v[0]=v0; v[1]=v1; }
和 TEA 很像,二者区别最简单的方法看 sum += delta 的位置
XXTEA
#define DELTA 0x9e3779b9 #define MX ((z>>5^y<<2) + (y>>3^z<<4) ^ (sum^y) + (k[p&3^e]^z)) long btea(long* v, long n, long* k) { unsigned long z=v[n-1], y=v[0], sum=0, e; long p, q ; if (n > 1) { /* Coding Part */ q = 6 + 52/n; while (q-- > 0) { sum += DELTA; e = (sum >> 2) & 3; for (p=0; p<n-1; p++) y = v[p+1], z = v[p] += MX; y = v[0]; z = v[n-1] += MX; } return 0 ; } else if (n < -1) { /* Decoding Part */ n = -n; q = 6 + 52/n; sum = q*DELTA ; while (sum != 0) { e = (sum >> 2) & 3; for (p=n-1; p>0; p--) z = v[p-1], y = v[p] -= MX; z = v[n-1]; y = v[0] -= MX; sum -= DELTA; } return 0; } return 1; }
一般来说,识别可以通过,delta 以及 round = 6 + 52/n 、(sum >> 2) & 3这种特殊的运算来判断。
DES
详细的实现介绍可以看之前组会分享的 PPT
CTF DES加密 .pdf
主要通过 S盒 以及各个置乱表来识别,可以使用插件来自动化识别这些特征。
AES
AES(Advanced Encryption Standard,高级加密标准),分组大小是 128 位,根据密钥长度和轮数可以分为 AES-128、AES-192、AES-256,具体区别如下表:
| AES-128 | AES-192 | AES-256 | |
|---|---|---|---|
| 密钥长度(bit) | 128 | 192 | 256 |
| 轮数 | 10 | 12 | 14 |
整体流程
整体来说AES加密有如下几步
- 密钥拓展,使用密钥拓展算法通过初始密钥获取轮密钥
- 初始轮密钥加
- 前 9 (或 11,或 13 ) 轮
- S 盒代换(SubBytes )
- 行移位 (ShiftRows )
- 列混合 (MixColumns )
- 轮密钥加(AddRoundKey)
- 最后一轮
- S 盒代换(SubBytes )
- 行移位 (ShiftRows )
- 轮密钥加(AddRoundKey)
每个步骤详解
下面分别对每个步骤进行介绍
- SubBytes—通过一个非线性的替换函数,用查找表的方式把每个字节替换成对应的字节。
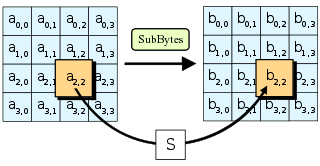
- ShiftRows—将矩阵中的每行进行循环移位。
- 第 1 行不变,第 2 行循环左移 1, 第 3 行 循环左移 2, 第 4 行循环左移 3
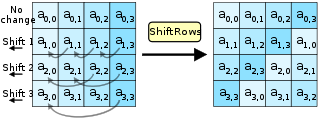
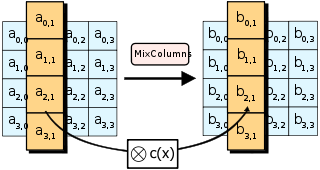
- MixColumns—使用可逆线性转换将状态每一列的四个字节混合在一起,输入输出都是 4 个字节(也就是1列)。
- 变换公式如下:

各个值在相加时使用的是模2加法(异或运算)
- 更一般的,可以认为是把每列看作
上的多项式,让其与一个固定的多项式
相乘,然后模
,通过运算可以证明此运算与上述矩阵运算等价
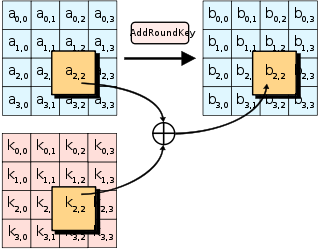
- AddRoundKey—矩阵中的每一个字节都与该轮的轮密钥(round key)做xor运算;每个子密钥由密钥生成方案产生。
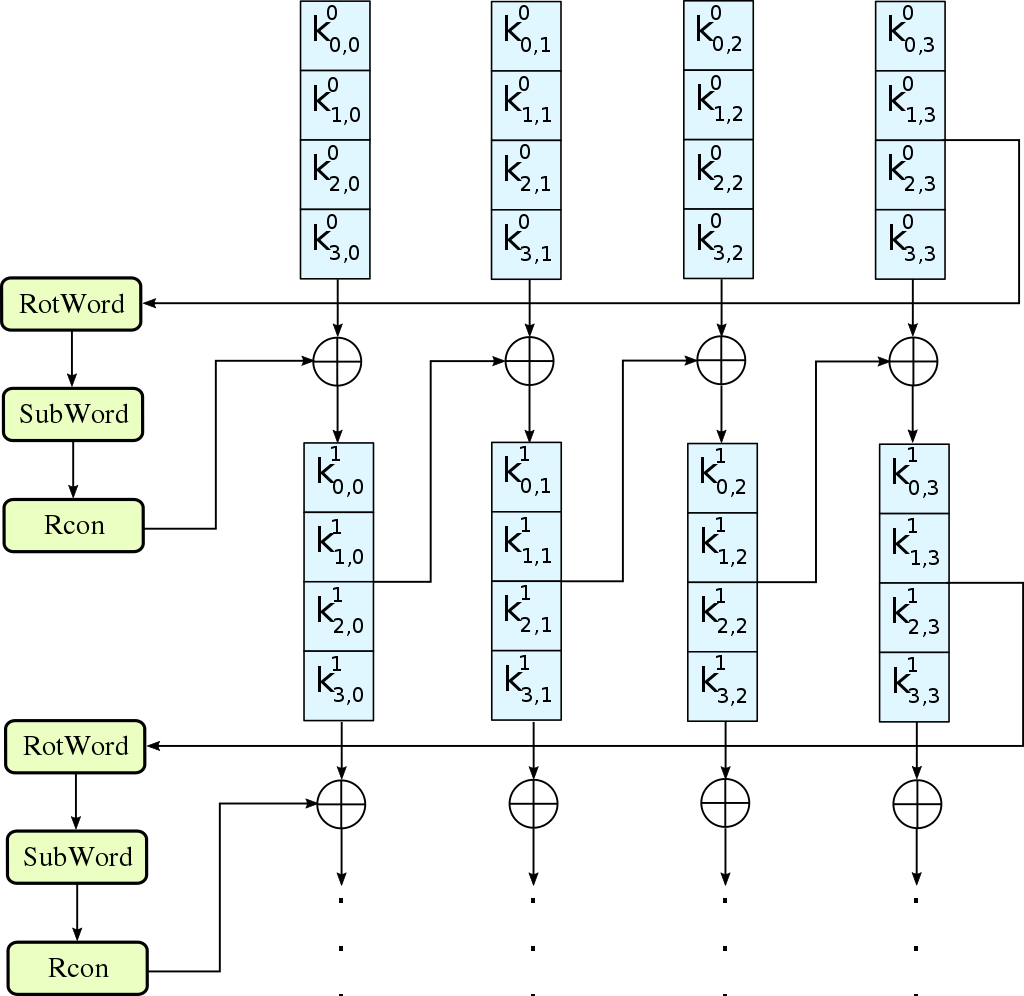
轮密钥生成算法
每个轮密钥是 128 bit,
uint8_t R[] = {0x02, 0x00, 0x00, 0x00}; uint8_t * Rcon(uint8_t i) { if (i == 1) { R[0] = 0x01; // x^(1-1) = x^0 = 1 } else if (i > 1) { R[0] = 0x02; i--; while (i > 1) { R[0] = gmult(R[0], 0x02); i--; } } return R; } void sub_word(uint8_t *w) { uint8_t i; for (i = 0; i < 4; i++) { w[i] = s_box[w[i]]; } } void rot_word(uint8_t *w) { uint8_t tmp; uint8_t i; tmp = w[0]; for (i = 0; i < 3; i++) { w[i] = w[i+1]; } w[3] = tmp; } void coef_add(uint8_t a[], uint8_t b[], uint8_t d[]) { d[0] = a[0]^b[0]; d[1] = a[1]^b[1]; d[2] = a[2]^b[2]; d[3] = a[3]^b[3]; } void aes_key_expansion(uint8_t *key, uint8_t *w) { uint8_t tmp[4]; uint8_t i; uint8_t len = Nb*(Nr+1); for (i = 0; i < Nk; i++) { w[4*i+0] = key[4*i+0]; w[4*i+1] = key[4*i+1]; w[4*i+2] = key[4*i+2]; w[4*i+3] = key[4*i+3]; } for (i = Nk; i < len; i++) { tmp[0] = w[4*(i-1)+0]; tmp[1] = w[4*(i-1)+1]; tmp[2] = w[4*(i-1)+2]; tmp[3] = w[4*(i-1)+3]; if (i % Nk == 0) { rot_word(tmp); sub_word(tmp); coef_add(tmp, Rcon(i / Nk), tmp); } else if (Nk > 6 && i % Nk == 4) { sub_word(tmp); } w[4*i+0] = w[4*(i-Nk)+0]^tmp[0]; w[4*i+1] = w[4*(i-Nk)+1]^tmp[1]; w[4*i+2] = w[4*(i-Nk)+2]^tmp[2]; w[4*i+3] = w[4*(i-Nk)+3]^tmp[3]; } }
Rcon 也可以用以下的表格来实现
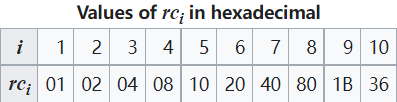
优化算法
类似前面介绍的DES加密的SP盒,AES也有着类似的优化算法,除了轮密钥加,以下三个步骤
- S 盒代换(SubBytes )
- 行移位 (ShiftRows )
- 列混合 (MixColumns )
可以合并为一步表格置换叫做 Te 表
白盒 AES
只见过一次,2022年国赛分区赛逆向有个,解法可以参考下面的文章:
https://bbs.pediy.com/thread-254042.htm
SM4
SM4是国密算法,由国家密码局发布,分组长度为128比特,密钥长度为128比特。
这个加密在22年的比赛中还没遇到过,但是还是简单介绍下
轮函数
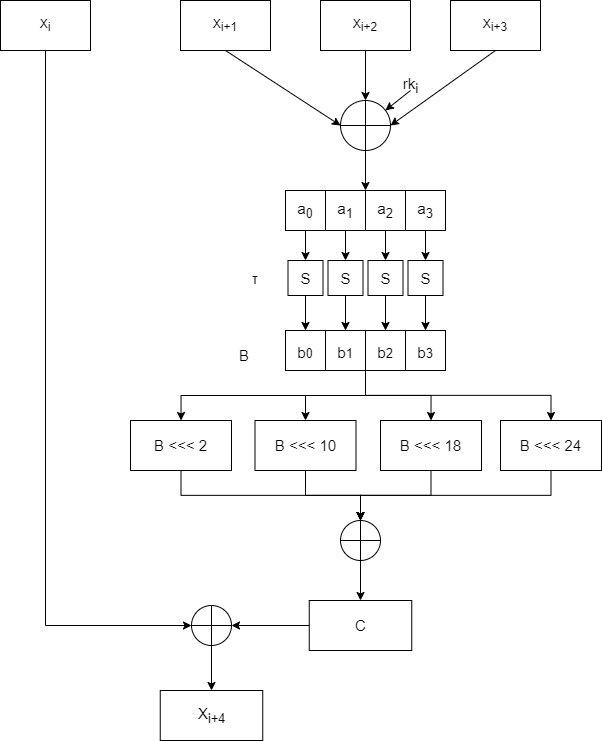
密钥拓展算法
T' 和合成置换T基本类似,只是换了线性置换L为L'
static const uint32_t FK[4] = {0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc}; static const uint32_t CK[32] = { 0x00070E15, 0x1C232A31, 0x383F464D, 0x545B6269, 0x70777E85, 0x8C939AA1, 0xA8AFB6BD, 0xC4CBD2D9, 0xE0E7EEF5, 0xFC030A11, 0x181F262D, 0x343B4249, 0x50575E65, 0x6C737A81, 0x888F969D, 0xA4ABB2B9, 0xC0C7CED5, 0xDCE3EAF1, 0xF8FF060D, 0x141B2229, 0x30373E45, 0x4C535A61, 0x686F767D, 0x848B9299, 0xA0A7AEB5, 0xBCC3CAD1, 0xD8DFE6ED, 0xF4FB0209, 0x10171E25, 0x2C333A41, 0x484F565D, 0x646B7279 };
识别方法
由上面的介绍,可以看出,SM4也有着 S盒、FK、CK几个常量表,所以使用插件也可以自动化识别。
分组密码的工作模式
密码学中,分组密码的工作模式(mode of operation)允许使用同一个分组密码密钥对多于一块的数据进行加密,并保证其安全性。
分组密码自身只能加密长度等于密码分组长度的单块数据,若要加密变长数据,则数据必须先被划分为一些单独的密码块。通常而言,最后一块数据也需要使用合适填充方式将数据扩展到符合密码块大小的长度。一种工作模式描述了加密每一数据块的过程,并常常使用基于一个通常称为初始化向量的附加输入值以进行随机化,以保证安全。
电子密码本(ECB)
最简单的加密模式即为电子密码本(Electronic codebook,ECB)模式。需要加密的消息按照块密码的块大小被分为数个块,并对每个块进行独立加密。
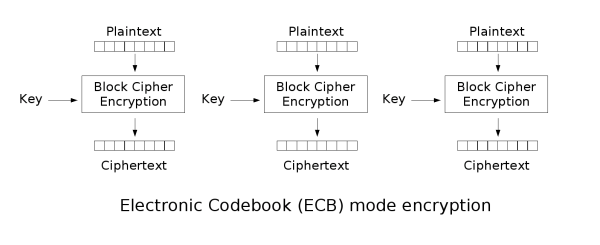
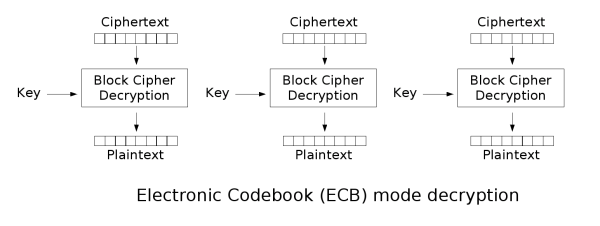
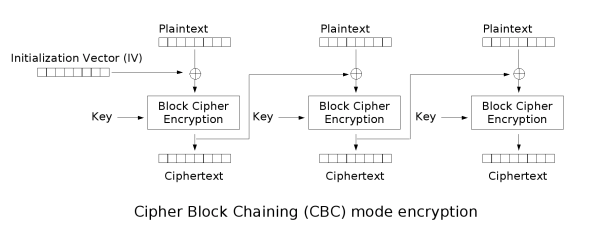
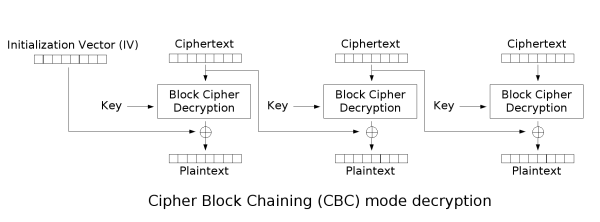
密码块链接(CBC)
在CBC模式中,每个明文块先与前一个密文块进行异或后,再进行加密。在这种方法中,每个密文块都依赖于它前面的所有明文块。同时,为了保证每条消息的唯一性,在第一个块中需要使用初始化向量。
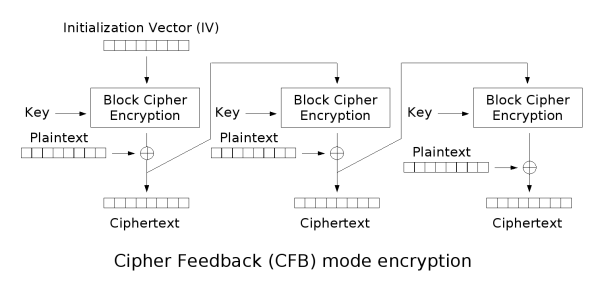
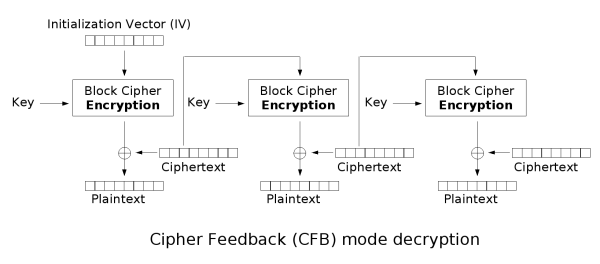
密文反馈(CFB)
密文反馈(CFB,Cipher feedback)模式类似于CBC,可以将块密码变为自同步的流密码;工作过程亦非常相似,CFB的解密过程几乎就是颠倒的CBC的加密过程:
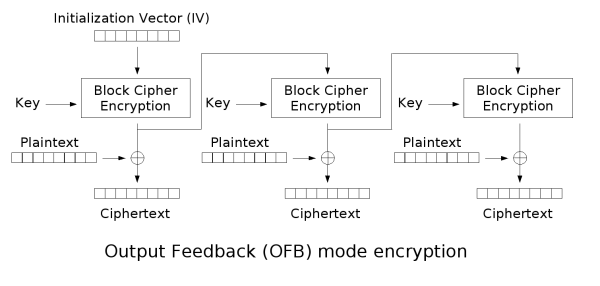
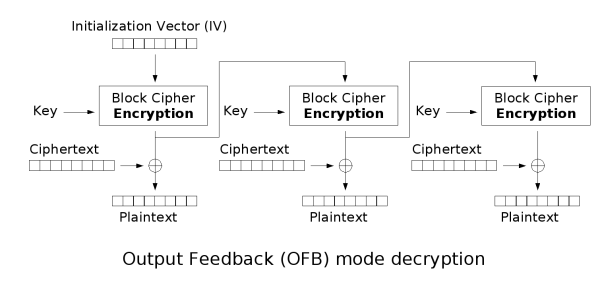
输出反馈(OFB)
输出反馈模式(Output feedback, OFB)可以将块密码变成同步的流密码。它产生密钥流的块,然后将其与明文块进行异或,得到密文。与其它流密码一样,密文中一个位的翻转会使明文中同样位置的位也产生翻转。这种特性使得许多错误校正码,例如奇偶校验位,即使在加密前计算,而在加密后进行校验也可以得出正确结果。
非对称密码
RSA
产生公钥和私钥:
- 随机选择两个大素数
和
,且
,计算
- 求得
- 选择一个小于
的整数
,使
与
互质。求
,令
(e, N) 是公钥,(d,N) 是私钥
加密
解密
识别
对于RSA的识别,关键是对于大数运算库函数的识别,常见的大数运算库有:GMP、Miracl
或者一些密码学的库 OpenSSL、Crypto++、libtomcrypt(用的GMP) 也有着对应的实现。
单向散列函数
MD5
MD5消息摘要算法(MD5,Message-Digest Algorithm),一种被广泛使用的密码散列函数,可以产生出一个128位(16 bytes)的散列值。
下面是C语言具体实现:
// Constants are the integer part of the sines of integers (in radians) * 2^32. const uint32_t k[64] = { 0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501, 0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821, 0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa, 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8, 0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a, 0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70, 0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05, 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665, 0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1, 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1, 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391 }; // r specifies the per-round shift amounts const uint32_t r[] = {7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21}; #define LEFTROTATE(x, c) (((x) << (c)) | ((x) >> (32 - (c)))) void to_bytes(uint32_t val, uint8_t *bytes) { bytes[0] = (uint8_t) val; bytes[1] = (uint8_t) (val >> 8); bytes[2] = (uint8_t) (val >> 16); bytes[3] = (uint8_t) (val >> 24); } uint32_t to_int32(const uint8_t *bytes) { return (uint32_t) bytes[0] | ((uint32_t) bytes[1] << 8) | ((uint32_t) bytes[2] << 16) | ((uint32_t) bytes[3] << 24); } void md5(const uint8_t *initial_msg, size_t initial_len, uint8_t *digest) { // These vars will contain the hash uint32_t h0, h1, h2, h3; // Message (to prepare) uint8_t *msg = NULL; size_t new_len, offset; uint32_t w[16]; uint32_t a, b, c, d, i, f, g, temp; // Initialize variables - simple count in nibbles: h0 = 0x67452301; h1 = 0xefcdab89; h2 = 0x98badcfe; h3 = 0x10325476; //Pre-processing: //append "1" bit to message //append "0" bits until message length in bits ≡ 448 (mod 512) //append length mod (2^64) to message for (new_len = initial_len + 1; new_len % (512/8) != 448/8; new_len++); msg = (uint8_t*)malloc(new_len + 8); memcpy(msg, initial_msg, initial_len); msg[initial_len] = 0x80; // append the "1" bit; most significant bit is "first" for (offset = initial_len + 1; offset < new_len; offset++) msg[offset] = 0; // append "0" bits // append the len in bits at the end of the buffer. to_bytes(initial_len*8, msg + new_len); // initial_len>>29 == initial_len*8>>32, but avoids overflow. to_bytes(initial_len>>29, msg + new_len + 4); // Process the message in successive 512-bit chunks: //for each 512-bit chunk of message: for(offset=0; offset<new_len; offset += (512/8)) { // break chunk into sixteen 32-bit words w[j], 0 ≤ j ≤ 15 for (i = 0; i < 16; i++) w[i] = to_int32(msg + offset + i*4); // Initialize hash value for this chunk: a = h0; b = h1; c = h2; d = h3; // Main loop: for(i = 0; i<64; i++) { if (i < 16) { f = (b & c) | ((~b) & d); // F g = i; } else if (i < 32) { f = (d & b) | ((~d) & c); // G g = (5*i + 1) % 16; } else if (i < 48) { f = b ^ c ^ d; // H g = (3*i + 5) % 16; } else { f = c ^ (b | (~d)); // I g = (7*i) % 16; } temp = d; d = c; c = b; b = b + LEFTROTATE((a + f + k[i] + w[g]), r[i]); a = temp; } // Add this chunk's hash to result so far: h0 += a; h1 += b; h2 += c; h3 += d; } // cleanup free(msg); //var char digest[16] := h0 append h1 append h2 append h3 //(Output is in little-endian) to_bytes(h0, digest); to_bytes(h1, digest + 4); to_bytes(h2, digest + 8); to_bytes(h3, digest + 12); }
识别
首先常数 0x67452301, 0xefcdab89, 0x98badcfe, 0x10325476,是识别MD5的一大关键,其次就是 k 和 r 两个表(这俩不一定会写成数组的格式,也有可能硬编码到代码里),一般来说MD5是可以通过插件识别的。
SHA
安全散列算法(Secure Hash Algorithm,缩写为SHA)是一个密码散列函数家族,是FIPS所认证的安全散列算法。
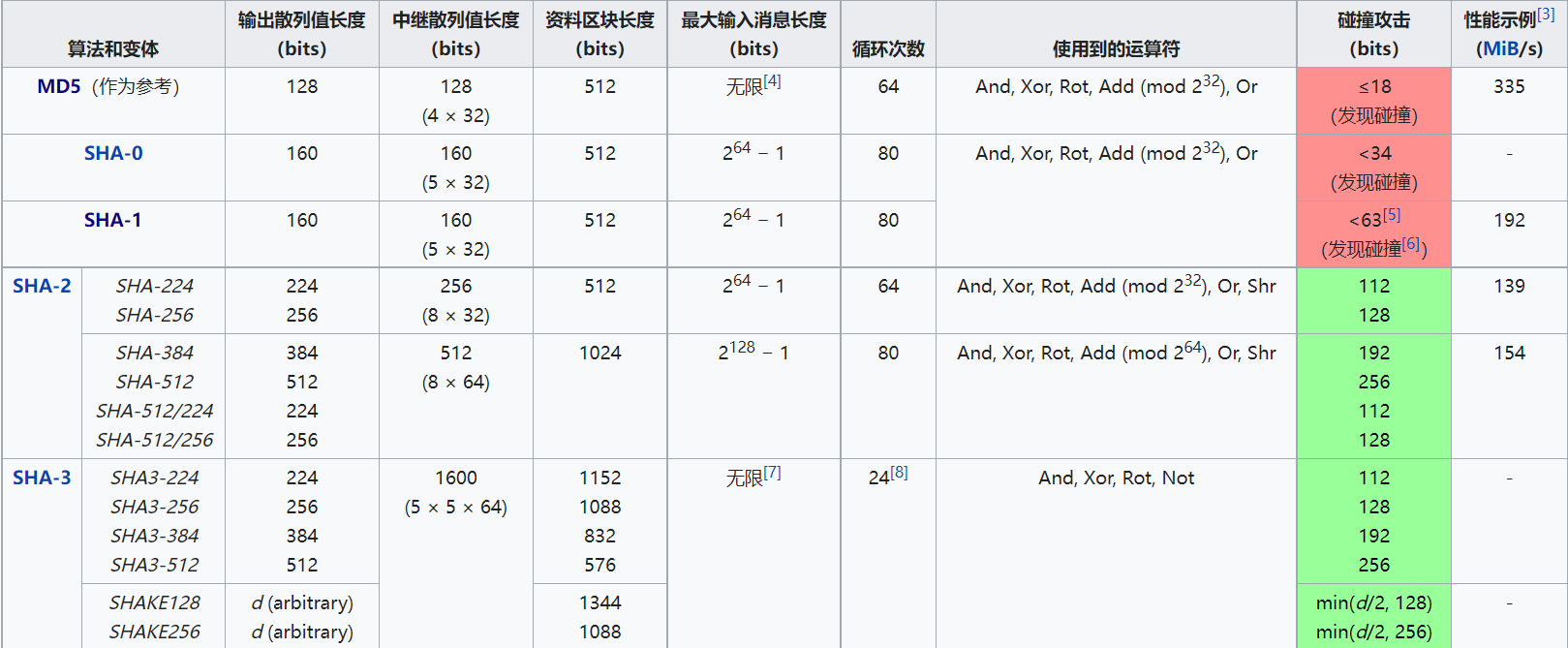
比较常见的有 SHA-1, SHA2-256,SHA2-512,下面是他们的特征:
// SHA-1 的初始散列值 uint32_t h[5] = {0x67452301, 0xEFCDAB89, 0x98BADCFE, 0x10325476, 0xC3D2E1F0}; // SHA2-256 的初始散列值 uint32_t h[8] = {0x6a09e667, 0xbb67ae85, 0x3c6ef372, 0xa54ff53a, 0x510e527f, 0x9b05688c, 0x1f83d9ab, 0x5be0cd19}; // SHA2-512 的初始散列值 uint64_t h[8] = {0x6a09e667f3bcc908, 0xbb67ae8584caa73b, 0x3c6ef372fe94f82b, 0xa54ff53a5f1d36f1, 0x510e527fade682d1, 0x9b05688c2b3e6c1f, 0x1f83d9abfb41bd6b, 0x5be0cd19137e2179};
太多啦,实现细节就不展开了,SHA2中 224和256实现相似,384和512实现相似,但是这四个的初始哈希值都是不一样的,只不过较短的都是截断了最后的 h7
识别
与 md5 类似(也是有表的只不过没列出来),就不再赘述了。
BaseXX 系列
Base64
Base64是网络上最常见的用于传输字节码的编码方式之一,Base64就是一种基于64个可打印字符来表示二进制数据的方法。它的工作方式可以简单的用wiki上的三张图来描述:
- 待加密数据字节数是 3 的整数倍,3 * 8 = 4 * 6,即最完美的情况,不需要Padding
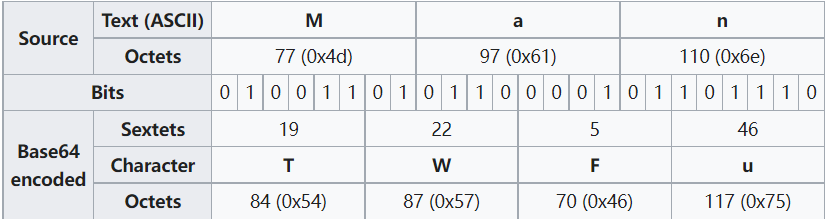
- len % 3 = 2,2 * 8 + 2 = 3 * 6, 即需要补 2 个 0,此时后面要添加 1 个等号作为标志
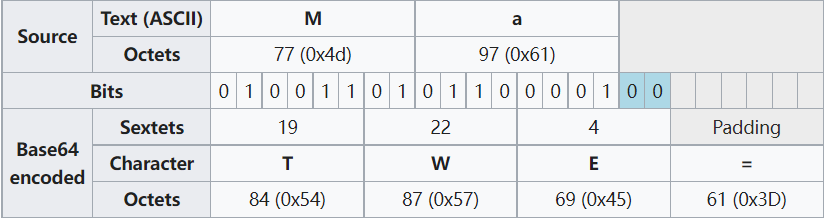
- len % 3 = 1,1 * 8 + 4 = 2 * 6, 即需要补 4 个 0,此时后面要添加 2 个等号作为标志

常见实现
unsigned int base64_encode(const unsigned char *in, unsigned int inlen, char *out) { int s; unsigned int i; unsigned int j; unsigned char c; unsigned char l; s = 0; l = 0; for (i = j = 0; i < inlen; i++) { c = in[i]; switch (s) { case 0: s = 1; out[j++] = base64en[(c >> 2) & 0x3F]; break; case 1: s = 2; out[j++] = base64en[((l & 0x3) << 4) | ((c >> 4) & 0xF)]; break; case 2: s = 0; out[j++] = base64en[((l & 0xF) << 2) | ((c >> 6) & 0x3)]; out[j++] = base64en[c & 0x3F]; break; } l = c; } switch (s) { case 1: out[j++] = base64en[(l & 0x3) << 4]; out[j++] = BASE64_PAD; out[j++] = BASE64_PAD; break; case 2: out[j++] = base64en[(l & 0xF) << 2]; out[j++] = BASE64_PAD; break; } out[j] = 0; return j; }
char *b64_encode(const unsigned char *src, size_t len) { int i = 0; int j = 0; char *enc = NULL; size_t size = 0; unsigned char buf[4]; unsigned char tmp[3]; // alloc enc = (char *)b64_buf_malloc(); if (NULL == enc) { return NULL; } // parse until end of source while (len--) { // read up to 3 bytes at a time into `tmp' tmp[i++] = *(src++); // if 3 bytes read then encode into `buf' if (3 == i) { buf[0] = (tmp[0] & 0xfc) >> 2; buf[1] = ((tmp[0] & 0x03) << 4) + ((tmp[1] & 0xf0) >> 4); buf[2] = ((tmp[1] & 0x0f) << 2) + ((tmp[2] & 0xc0) >> 6); buf[3] = tmp[2] & 0x3f; // allocate 4 new byts for `enc` and // then translate each encoded buffer // part by index from the base 64 index table // into `enc' unsigned char array enc = (char *)b64_buf_realloc(enc, size + 4); for (i = 0; i < 4; ++i) { enc[size++] = b64_table[buf[i]]; } // reset index i = 0; } } // remainder if (i > 0) { // fill `tmp' with `\0' at most 3 times for (j = i; j < 3; ++j) { tmp[j] = '\0'; } // perform same codec as above buf[0] = (tmp[0] & 0xfc) >> 2; buf[1] = ((tmp[0] & 0x03) << 4) + ((tmp[1] & 0xf0) >> 4); buf[2] = ((tmp[1] & 0x0f) << 2) + ((tmp[2] & 0xc0) >> 6); buf[3] = tmp[2] & 0x3f; // perform same write to `enc` with new allocation for (j = 0; (j < i + 1); ++j) { enc = (char *)b64_buf_realloc(enc, size + 1); enc[size++] = b64_table[buf[j]]; } // while there is still a remainder // append `=' to `enc' while ((i++ < 3)) { enc = (char *)b64_buf_realloc(enc, size + 1); enc[size++] = '='; } } // Make sure we have enough space to add '\0' character at end. enc = (char *)b64_buf_realloc(enc, size + 1); enc[size] = '\0'; return enc; }
识别
- 有
ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/码表(或者类似的长度是64就行) - 基本上实现就是上面两种形式,对照一下就行
比如下面这个,显然就是上面的第一种形式
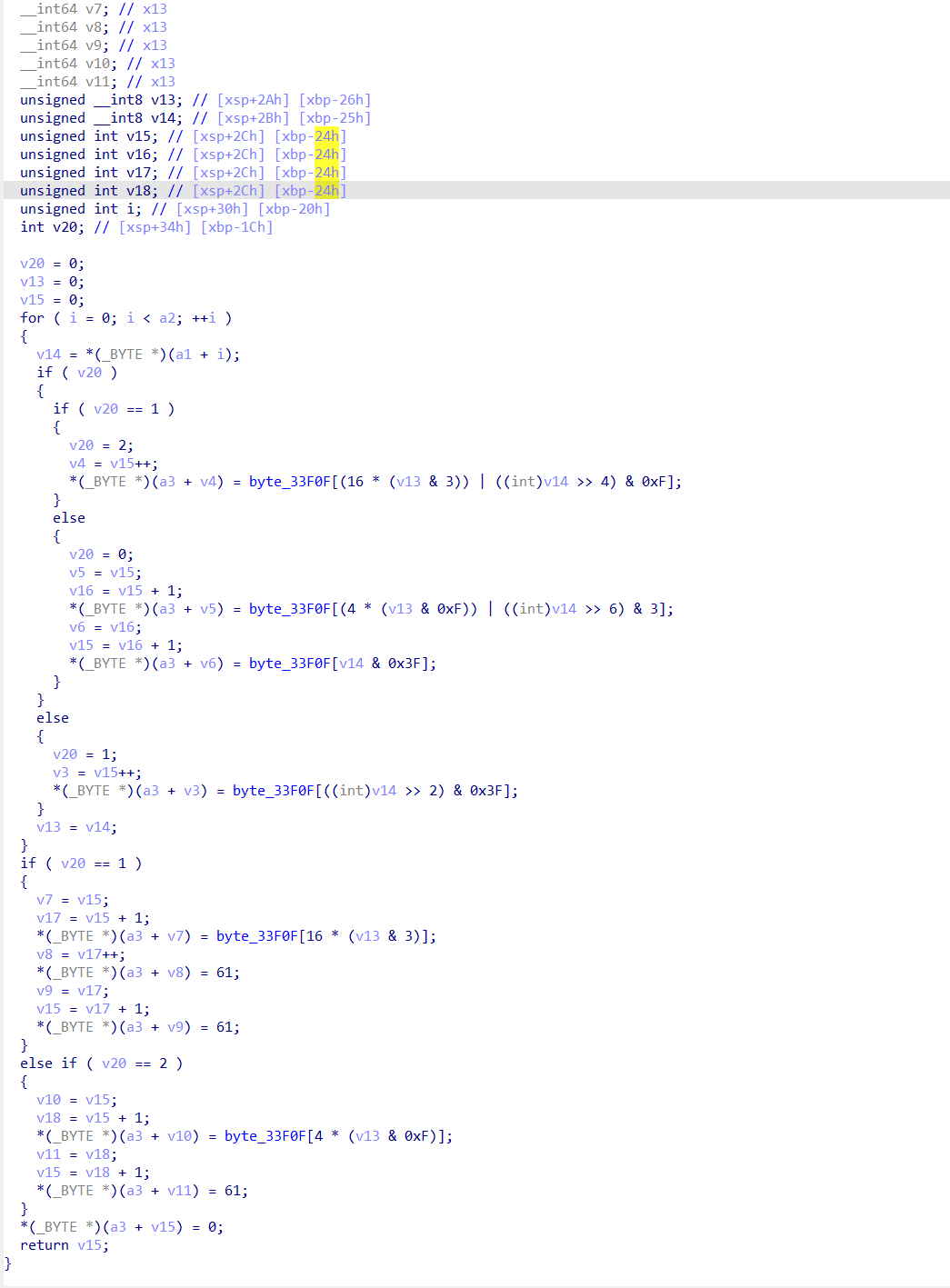
Base32
就是把 Base64 的 3 * 8 = 4 * 6 改成 5 * 8 = 8 * 5 而已,不再展开。
Base58
static const char b58digits_ordered[] = "123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz"; bool b58enc(char *b58, size_t *b58sz, const void *data, size_t binsz) { const uint8_t *bin = data; int carry; size_t i, j, high, zcount = 0; size_t size; while (zcount < binsz && !bin[zcount]) ++zcount; size = (binsz - zcount) * 138 / 100 + 1; uint8_t buf[size]; memset(buf, 0, size); for (i = zcount, high = size - 1; i < binsz; ++i, high = j) { for (carry = bin[i], j = size - 1; (j > high) || carry; --j) { carry += 256 * buf[j]; buf[j] = carry % 58; carry /= 58; if (!j) { // Otherwise j wraps to maxint which is > high break; } } } for (j = 0; j < size && !buf[j]; ++j); if (*b58sz <= zcount + size - j) { *b58sz = zcount + size - j + 1; return false; } if (zcount) memset(b58, '1', zcount); for (i = zcount; j < size; ++i, ++j) b58[i] = b58digits_ordered[buf[j]]; b58[i] = '\0'; *b58sz = i + 1; return true; }
关键特征为长度为 58 的码表 ,和 mod 58 、 除以 58 操作,以及奇怪的 * 138 / 100 + 1
比如下面这个
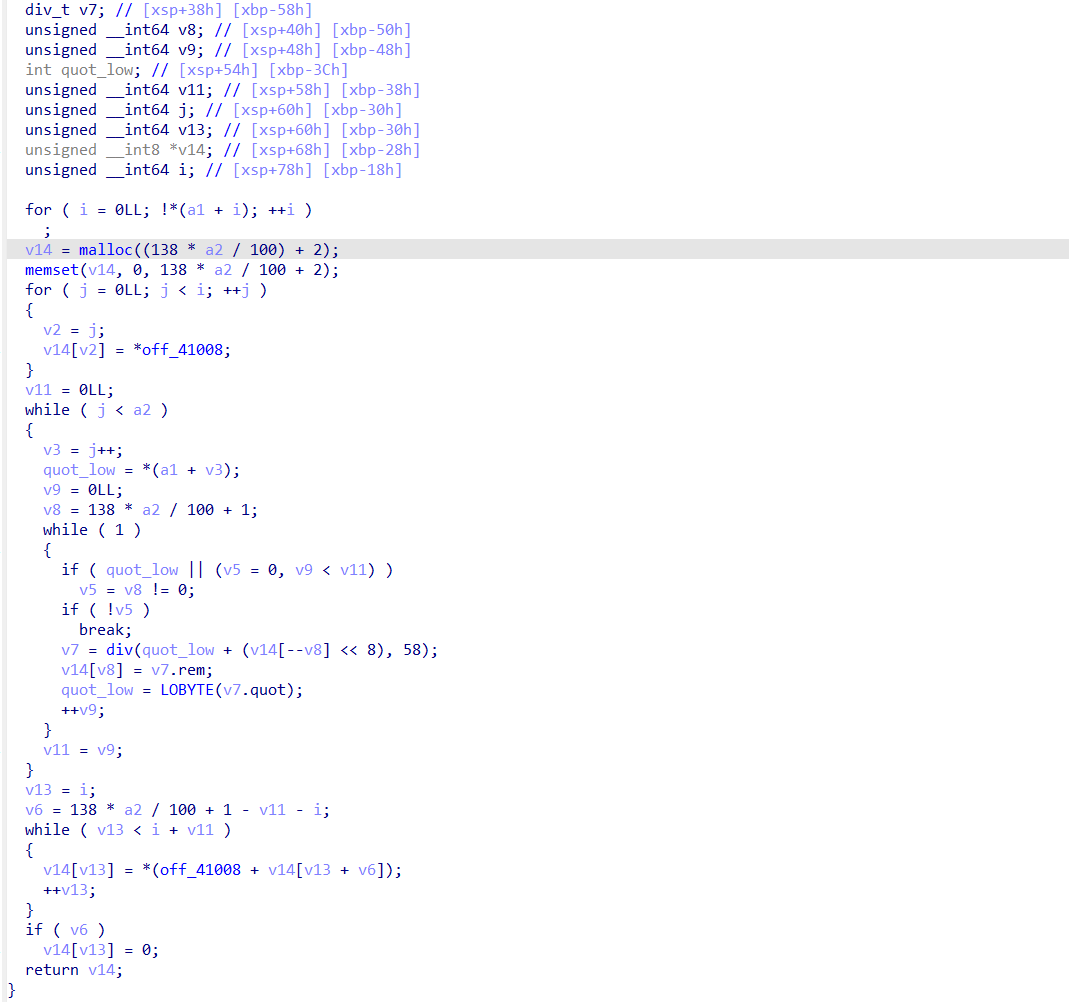
Base24
Base24实现非常简单,简单到没必要了解,因为只需要看一下加密,就能写出来解密。
但是还是给一下实现:
const char base24code[] = { 'B','C','D','F','G', 'H','J','K','M','P', 'Q','R','T','V','W', 'X','Y','2','3','4', '6','7','8','9', '\0' }; char *base24encode(char *buf, unsigned char *byst, size_t sizeOfBytes) { int i = 0; unsigned char *p = byst; while ((size_t)(i = (p-byst)) < sizeOfBytes) { buf[2*i] = base24code[((*p) >> 4)]; buf[(2*i)+1] = base24code[23 - ((*p) & 0x0f)]; p++; } buf[(2*i)+1] = '\0'; return buf; }
循环冗余码
CRC32
一般的实现就是两种,查表的,还有不用表的
uint32_t crc32(const void* buf, size_t size) { const uint8_t* p = buf; uint32_t crc = ~0U; while (size--) { crc = crc32_tab[(crc ^ *p++) & 0xFF] ^ (crc >> 8); } return ~crc; }
uint crc32(byte *data, int size) { uint r = ~0; byte *end = data + size; while(data < end) { r ^= *data++; for(int i = 0; i < 8; i++) { uint t = ~((r&1) — 1); r = (r>>1) ^ (0xEDB88320 & t); } } return ~r; }

















