抛物线正等测投影数值解的求法

背景：为锻炼代同学，老师给了她一个反向工程微信“跳一跳”小游戏的任务，希望做一个一样的出来。跳一跳中，有方块，有小人，小人站在方块上。

这个游戏的玩法是，用手指按住手机屏幕，松开手指小人飞出。随着屏幕按压时间的增加，跳跃距离也会增加。

做出猜测

感谢代同学提供图片。
根据生活常识，物体在空中飞行的轨迹是一条抛物线。

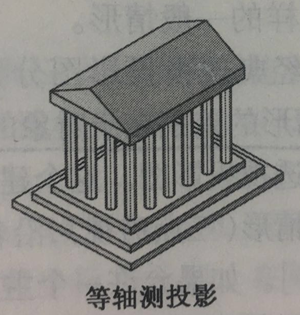
观察到游戏中的抛物线并不对称，猜测它是在三维空间建模投影到一个平面上的。看《交互式计算机图形学》（Edward Angel，交互式计算机图形学，电子工业出版社，2012.5，p141）中，正等测（正等测等价于等轴测）的例子和跳一跳游戏中方块（上图）很相似，猜测它使用的是三维空间正等测投影到二维平面上的投影。假设跳一跳的方块是由三维直角坐标系下的方块做正等测投影得到的，观察跳一跳方块中朝向我们的角，三个角都是120度，这和正等测的定义相符合。

矩阵与坐标变换

在计算机图形学中，三维的点用四维齐次坐标表示。点的投影，可以通过点左乘一个变换矩阵来实现。正等测的变换矩阵是：

如何使用它呢？

附一段matlab代码及其执行的结果。

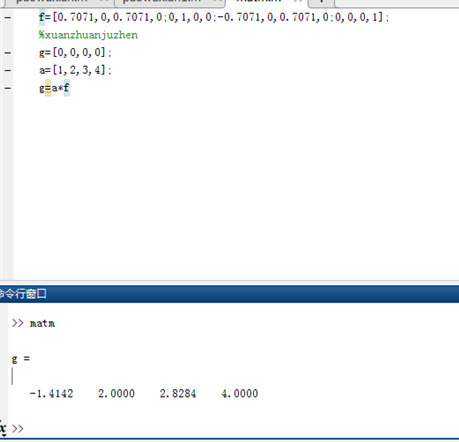
数值解的基本思路—采样与近似

求出抛物线在三维空间中的方程，等间距采样200个点。
在数值计算中，由于函数的定义域集合大小通常为无穷大，我们不可能计算出每一个点。在本文关注的问题中也是如此。我们等间距的在抛物线上选取200个点，并保证这200个点关于对称轴对称。由于现实生活经验中，在地面抛出落在地面的抛物线段也满足“关于对称轴对称”，故我们这样采样。

采样是为了近似表现曲线。曲线是由点组成的，我们已知这些点，把这些点用平滑的曲线连接起来，就成了曲线。

然后把每个被采样的三维空间中抛物线上的点乘以变换矩阵，投影到平面上。投影后的点，是二维平面上抛物线上的点。

由于手机屏幕不大，直接在200个点中选取一些，作为旗子跳跃动画中棋子坐标是可以接受的。假设动画时长2秒，一秒30帧，那么60帧也就是60个点是完全够用的。