线性代数:方程组的几何解释
感谢笛卡尔让代数和几何结合起来。
大学的时候讲矩阵感觉就是突然进入一个新的世界,和以前的世界没有任何的联系,我认为任何的新知识如果不能用旧的知识去引导,去结合,那么这个知识一定难以理解。感谢Gilbert Strang以一种循序渐进的讲课方式把线性方程组和矩阵进行了结合。
线性方程组忘记是哪个阶段的知识了,才开始是使用消元法进行解方程组,后来使用几何的方式来表示这种方式。就是在笛卡尔坐标系上划线,这应该是初中知识,当然也会划曲线和直线的交叉,这不是线性方程组的领域了,参考百度百科线性方程的解释,线性方程也称一次方程。指未知数都是一次的方程。其一般的形式是ax+by+...+cz+d=0。线性方程的本质是等式两边乘以任何相同的非零数,方程的本质都不受影响。这也许就是这门学科叫线性代数的原因。
线性方程组一定有解吗?,答案是不一定,我依然记得当时考试的时候经常遇到无解的方程组,老师一个考场一个考场的通知把某个变量的系数修改下。
线性方程组和矩阵结合
通过把线性方程组系数抽出来形成一个矩阵然后乘上未知数的列向量
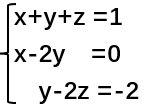 =》
=》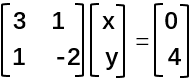 =》Ax=b
=》Ax=b线性方程组图表示
就像初中一行,我们需要在笛卡尔坐标系中画出方程组的解。
行图
和初中一样,一次在坐标系中画出一个方程的线。相交的地方就是方程组的解。
列图
在画列图之间,要把矩阵转成向量的方式。
 =》
=》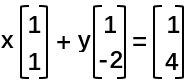
图形如下
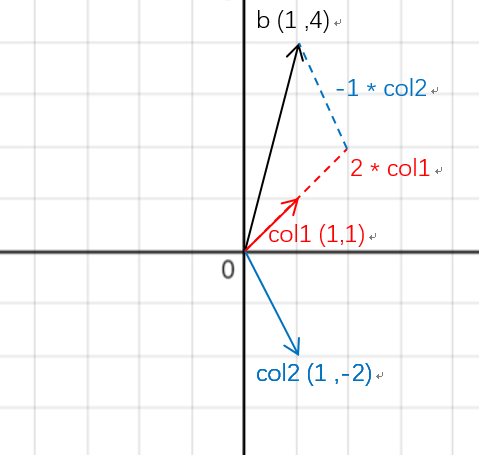
老头有句话不错:
矩阵乘以向量的结果是矩阵列的线性组合
我的理解
矩阵乘与矩阵结果是矩阵乘与向量的结合



 浙公网安备 33010602011771号
浙公网安备 33010602011771号