直接法

 前言

　　直接法是视觉里程计另一主要分支，它与特征点法有很大不同。随着SVO、LSD-SLAM等直接法SLAM方案的流行，直接法本身也得到越来越多的关注。特征点法与直接究竟谁更好一些，是近年视觉里程计研究领域一个非常有趣的问题。本讲，我们将介绍直接法的原理，并利用g2o实现基于直接法的视觉里程计。

---

 1. 直接法的引出

　　尽管特征点法在视觉里程计中占据主流地位，研究者们认识它至少有以下几个缺点：

1. 关键点的提取与描述子的计算非常耗时。实践当中，SIFT目前在CPU上是无法实时计算的，而ORB也需要近20毫秒的计算。如果整个SLAM以30毫秒/帧的速度运行，那么一大半时间都花在计算特征点上。
2. 使用特征点时，忽略了除特征点以外的所有信息。一张图像有几十万个像素，而特征点只有几百个。只使用特征点丢弃了大部分可能有用的图像信息。
3. 相机有时会运动到特征缺失的地方，往往这些地方都没有什么明显的纹理信息。例如，有时我们会面对一堵白墙，或者一个空荡荡的走廓。这些场景下特征点数量会明显减少，我们可能找不到足够的匹配点来计算相机运动。

　　我们看到使用特征点确实存在一些问题。针对这些缺点，也存在若干种可行的方法：

1. 只计算关键点，不计算描述子。同时，使用光流法（Optical Flow）来跟踪特征点的运动。这样可以回避计算和匹配描述子带来的时间，但光流本身的计算需要一定时间；
2. 只计算关键点，不计算描述子。同时，使用直接法来计算特征点在下一时刻图像的位置。这同样可以跳过描述子的计算过程，而且直接法的计算更加简单。
3. 既不计算关键点、也不计算描述子——根据像素来直接计算相机运动。

　　第一种方法仍然使用特征点，只是把匹配描述子替换成了光流跟踪，估计相机运动时仍使用PnP或ICP算法。而在，后两个方法中，我们会根据图像的像素信息来计算相机运动，它们称为直接法。
　　使用特征点法估计相机运动时，我们把特征点看作固定在三维空间的不动点。根据它们在相机中的投影位置，通过最小化重投影误差（Reprojection error）来优化相机运动。在这个过程中，我们需要精确地知道空间点在两个相机中投影后的像素位置——这也就是我们为何要对特征进行匹配或跟踪的理由。而在直接法中，我们最小化的不再是重投影误差，而是测量误差（Phometric error）。
　　直接法是本讲介绍的重点。它的存在就是为了克服特征点法的上述缺点（虽然它会引入另一些问题）。直接法直接根据像素亮度信息，估计相机的运动，可以完全不用计算关键点和描述子。于是，直接法既避免了特征的计算时间，也避免了特征缺失的情况。只要场景中存在明暗变化（可以是渐变，不形成局部的图像特征），直接法就能工作。根据使用像素的数量，直接法分为稀疏、稠密和半稠密三种，具有恢复稠密结构的能力。相比于特征点法通常只能重构稀疏特征点，直接法和稠密重建有更紧密的联系。
　　历史上，虽然早期也有一些对直接法的使用，但直到RGB-D相机出现后，人们才发现直接法对RGB-D相机，进而对单目相机，都是行之有效的方法。随着一些使用直接法的开源项目的出现（如SVO、LSD-SLAM等），它们逐渐地走上主流舞台，成为视觉里程计算法中重要的一部分。

---

 2. 直接法数学推导

　　直接法和光流非常相似，它们都是基于灰度不变假设的：

灰度不变假设：同一个空间点的像素灰度，在各个图像中是固定不变的。

　　灰度不变假设是一个很强的假设，实际当中很可能不成立。事实上，由于物体的材质不同，像素会出现高光和阴影部分；有时，相机会自动调整曝光参数，使得图像整体变亮或变暗。这些时候灰度不变假设都是不成立的，因此直接法/光流的结果也不一定可靠。不过，暂且让我们认为该假设成立，从而看看如何计算相机的运动。我们先介绍直接法的原理，然后使用g2o实现直接法。

　　

　　考虑某个空间点 $P$ 和两个时刻的相机。$P$ 的世界坐标为 $[X,Y,Z]$，它在两个相机上成像，其非齐次像素坐标为 $\mathbf{p}_1, \mathbf{p}_2$。我们的目标是求第一个相机到第二个相机的相对位姿变换。设第一个相机旋转、平移为 $\mathbf{I}, \mathbf{0}$，第二个相机外参为 $\mathbf{R}, \mathbf{t}$（李代数为$\mathbf{\xi}$）。同时，两相机的内参相同，记为$\mathbf{K}$。为清楚起见，我们列写完整的投影方程：

\[{\mathbf{p}_1} = {\left[ \begin{array}{l}
    u\\
    v
    \end{array} \right]_1} = \mathbf{D} \frac{1}{Z_1} \mathbf{KP} \]
\[{\mathbf{p}_2} = {\left[ \begin{array}{l}
    u\\
    v
    \end{array} \right]_2} = \mathbf{D}\frac{1}{Z_2} \mathbf{K}\left( {\mathbf{RP} +\mathbf{t}} \right) = \mathbf{D}\frac{1}{Z_2} \mathbf{K} \exp \left( {{\mathbf{\xi} ^ \wedge }} \right) \mathbf{P}\]

　　其中 $Z_1,Z_2$ 是 $P$ 在两个相机坐标系下的深度坐标值。$\mathbf{D}$ 为齐次坐标到非齐次坐标的转换矩阵：
\[\begin{equation}
\mathbf{D} = \left[ {\begin{array}{*{20}{c}}
    1&0&0\\
    0&1&0
    \end{array}} \right]
\end{equation}\]

　　在直接法中，我们同样是解一个优化问题，但这个优化最小化的不是重投影误差，而是测量误差（Photometric Error），也就是 $P$ 的两个像的亮度误差：
\[\begin{equation}
e = {\mathbf{I}_1}\left( {{\mathbf{p}_1}} \right) - {\mathbf{I}_2}\left( {{\mathbf{p}_2}} \right)
\end{equation}\]

　　我们优化该误差的二范数：

\[\begin{equation}
\mathop {\min }\limits_{\mathbf{\xi}}  J\left( \mathbf{\xi}  \right) = { e^T} e
\end{equation}\]

 　　能够做这种优化的理由即灰度不变假设。在直接法中，我们假设一个空间点在各个视角下，成像的灰度是不变的。同样的，这依然是一个很强的假设，而且与光流法十分相似。实际当中，我们有许多个（比如$N$个）空间点$P_i$，那么，整个相机位姿估计问题变为：
\[\begin{equation}\label{key}
\mathop {\min }\limits_{\mathbf{\xi}}  J\left( \mathbf{\xi}  \right) = \sum\limits_{i = 1}^N {e_i^T{e_i}}, \quad {e_i} = { \mathbf{I}_1}\left( {{\mathbf{p}_{1,i}}} \right) - {\mathbf{I}_2}\left( {{ \mathbf{p}_{2,i}}} \right)
\end{equation}\]

　　为了求解这个优化问题，我们关心误差$e$是如何随着相机位姿$\mathbf{\xi}$变化的，需要分析它们的导数关系。因此，使用李代数上的扰动模型。我们给$\exp (\mathbf{\xi})$左乘一个小扰动$\exp( \delta \mathbf{\xi} )$，得：

　　\[\begin{equation}\begin{array}{ll}
e\left( { \mathbf{\xi}  \oplus \delta \mathbf{\xi} } \right) &= { \mathbf{I} _1}\left( {\frac{1}{{{Z_1}}} \mathbf{DKP} } \right) - {\mathbf{I}_2}\left( {\frac{1}{{{Z_2}}} \mathbf{DK}\exp \left( {\delta {\mathbf{\xi} ^ \wedge }} \right)\exp \left( {{\mathbf{\xi} ^ \wedge }} \right) \mathbf{P}} \right)\\
& \approx {\mathbf{I}_1}\left( {\frac{1}{{{Z_1}}} \mathbf{DKP}} \right) - {\mathbf{I}_2}\left( {\frac{1}{{{Z_2}}} \mathbf{DK} \left( {1 + \delta {\mathbf{\xi} ^ \wedge }} \right)\exp \left( {{ \mathbf{\xi} ^ \wedge }} \right) \mathbf{P} } \right)\\
&= {\mathbf{I}_1}\left( {\frac{1}{{{Z_1}}} \mathbf{DKP}} \right) - {\mathbf{I}_2}\left( {\frac{1}{{{Z_2}}} \mathbf{DK}\exp \left( {{\mathbf{\xi} ^ \wedge }} \right) \mathbf{P} + \frac{1}{{{Z_2}}} \mathbf{DK} \delta { \mathbf{\xi} ^ \wedge }\exp \left( {{\mathbf{\xi} ^ \wedge }} \right) \mathbf{P}} \right)
\end{array}\end{equation}\]

　　记
\[\begin{equation}\begin{array}{ll}
\mathbf{q} &= \delta \mathbf{\xi} ^\wedge \exp \left( {{ \mathbf{\xi} ^ \wedge }} \right) \mathbf{P} \\
\mathbf{u} &= \frac{1}{{{Z_2}}} \mathbf{DK} \mathbf{q}
\end{array}\end{equation}\]

　　$\mathbf{q}$ 即 $P$ 在第二个相机坐标系下的坐标，而$\mathbf{u}$为它的像素坐标。于是，利用一阶泰勒展开，有：

\[\begin{equation}\begin{array}{ll}
e \left( { \mathbf{\xi}  \oplus \delta \mathbf{\xi} } \right) &= {\mathbf{I}_1}\left( {\frac{1}{{{Z_1}}} \mathbf{DKP}} \right) - {\mathbf{I}_2}\left( {\frac{1}{{{Z_2}}} \mathbf{DK} \exp \left( {{\mathbf{\xi} ^ \wedge }} \right) \mathbf{P} + \mathbf{u}} \right)\\
& \approx { \mathbf{I}_1}\left( {\frac{1}{{{Z_1}}} \mathbf{DKP}} \right) - {\mathbf{I}_2}\left( {\frac{1}{{{Z_2}}} \mathbf{DK}\exp \left( {{\mathbf{\xi} ^ \wedge }} \right) \mathbf{P}} \right) - \frac{{\partial { \mathbf{I}_2}}}{{\partial \mathbf{u}}}\frac{{\partial \mathbf{u}}}{{\partial \mathbf{q}}}\frac{{\partial \mathbf{q}}}{{\partial \delta \mathbf{\xi} }}\delta \mathbf{\xi} \\
&= e\left( \mathbf{\xi}  \right) - \frac{{\partial {\mathbf{I}_2}}}{{\partial \mathbf{u}}}\frac{{\partial \mathbf{u}}}{{\partial \mathbf{q}}}\frac{{\partial \mathbf{q}}}{{\partial \delta \mathbf{\xi} }}\delta \mathbf{\xi}
\end{array}\end{equation}\]

　　我们看到，一阶导数由于链式法则分成了三项，而这三项都是容易计算的：

1. $ \partial \mathbf{I}_2 / \partial \mathbf{u} $ 为$\mathbf{u}$处的像素梯度；
2.  $ \partial \mathbf{u} / \partial \mathbf{q} $ 为投影方程关于相机坐标系下的三维点的导数。我们把投影方程展开，为：    \[\begin{equation}
       u = \frac{{{f_x}X + {c_x}}}{Z},v = \frac{{{f_y}Y + {c_y}}}{Z}
       \end{equation}\]于是导数为：
       \[\begin{equation}
       \frac{{\partial \mathbf{u}}}{{\partial \mathbf{q}}} = \left[ {\begin{array}{*{20}{c}}
           {\frac{{\partial u}}{{\partial X}}}&{\frac{{\partial u}}{{\partial Y}}}&{\frac{{\partial u}}{{\partial Z}}}\\
           {\frac{{\partial v}}{{\partial X}}}&{\frac{{\partial v}}{{\partial Y}}}&{\frac{{\partial v}}{{\partial Z}}}
           \end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
           {\frac{{{f_x}}}{{\rm{Z}}}}&0&{ - \frac{{{f_x}X}}{{{Z^2}}}}\\
           0&{\frac{{{f_y}}}{Z}}&{ - \frac{{{f_y}Y}}{{{Z^2}}}}
           \end{array}} \right]
       \end{equation}\]
3. ${\partial \mathbf{q}}/{\partial \delta \mathbf{\xi} }$为变换后的三维点对变换的导数，这在李代数章节已经介绍过了：
       \[\begin{equation}
       \frac{{\partial \mathbf{q}}}{{\partial \delta \mathbf{\xi} }} = \left[ { \mathbf{I}, - {\mathbf{q}^ \wedge }} \right]
       \end{equation}\]

　　在实践中，由于后两项只与三维点$\mathbf{q}$有关，而与图像无关，我们经常把它合并在一起：

\[\begin{equation}
\frac{{\partial \mathbf{u}}}{{\partial \delta \mathbf{\xi} }} = \left[ {\begin{array}{*{20}{c}}
    {\frac{{{f_x}}}{Z}}&0&{ - \frac{{{f_x}X}}{{{Z^2}}}}&{ - \frac{{{f_x}XY}}{{{Z^2}}}}&{{f_x} + \frac{{{f_x}{X^2}}}{{{Z^2}}}}&{ - \frac{{{f_x}Y}}{Z}}\\
    0&{\frac{{{f_y}}}{Z}}&{ - \frac{{{f_y}Y}}{{{Z^2}}}}&{ - {f_y} - \frac{{{f_y}{Y^2}}}{{{Z^2}}}}&{\frac{{{f_y}XY}}{{{Z^2}}}}&{\frac{{{f_y}X}}{Z}}
    \end{array}} \right]
\end{equation}\]

　　于是，现在我们推导了误差相对于李代数的雅可比矩阵：

\[ \begin{equation}
\label{eq:jacobianofDirect}
\mathbf{J} =  - \frac{{\partial { \mathbf{I}_2}}}{{\partial \mathbf{u}}}\frac{{\partial \mathbf{u}}}{{\partial \delta \mathbf{\xi} }}
\end{equation}\]

对于$N$个点的问题，我们可以用这种方法计算优化问题的雅可比，然后使用G-N或L-M计算增量，迭代求解。例如，在G-N方法下，增量$\delta {\mathbf{\xi} ^*} $的计算方式为：
\[\begin{equation}
\left( {\sum\limits_{i = 1}^N { \mathbf{J}_i^T \mathbf{J}_i} } \right)\delta {\mathbf{\xi} ^*} =  - \sum\limits_{i = 1}^N {{\mathbf{J}_i^T}{e_i}}
\end{equation}\]
至此，我们推导了直接法估计相机位姿的整个流程，下面我们讲讲直接法是如何使用的。

---

 3. 直接法的使用

　　在我们上面的推导中，$P$是一个已知位置的空间点，它是怎么来的呢？在RGB-D相机下，我们可以把任意像素反投影到三维空间，然后投影到下一个图像中。如果在单目相机中，我们也可以使用已经估计好位置的特征点（虽然是特征点，但直接法里是可以避免计算描述子的）。根据$P$的来源，我们可以把直接法进行分类：

1. $P$来自于稀疏特征点，我们称之为稀疏直接法。通常我们使用数百个特征点，并且会像L-K光流那样，假设它周围像素也是不变的。这种稀疏直接法速度不必计算描述子，并且只使用数百个像素，因此速度最快，但只能计算稀疏的重构。
2. $P$来自部分像素。我们看到式（\ref{eq:jacobianofDirect}）中，如果像素梯度为零，整一项雅可比就为零，不会对计算运动增量有任何贡献。因此，可以考虑只使用带有梯度的像素点，舍弃像素梯度不明显的地方。这称之为半稠密（Semi-Dense）的直接法，可以重构一个半稠密结构。
3. $P$为所有像素，称为稠密直接法。稠密重构需要计算所有像素（一般几十万至几百万个），因此多数不能在现有的 CPU上实时计算，需要GPU的加速。

　　可以看到，从稀疏到稠密重构，都可以用直接法来计算。它们的计算量是逐渐增长的。稀疏方法可以快速地求解相机位姿，而稠密方法可以建立完整地图。具体使用哪种方法，需要视机器人的应用环境而定。

---

 4. 使用g2o实现直接法

　　现在，我们来演示如何使用稀疏的直接法。由于我们不涉及GPU编程，稠密的直接法就省略掉了。同时，为了保持程序简单，我们使用RGB-D数据而非单目数据，这样可以省略掉单目的深度恢复部分（这个很麻烦，我们之后另讲）。
　　求解直接法最后等价于求解一个优化问题，因此我们可以使用g2o这样的通用优化库帮助我们求解。在使用g2o之前，需要把直接法抽象成一个图优化问题。显然，直接法是由以下顶点和边组成的：

• 优化变量为一个相机位姿，因此需要一个位姿顶点。由于我们在推导中使用了李代数，故程序中使用李代数表达的$SE(3)$位姿顶点，如g2o/types/types\_six\_dof\_expmap.h中的“VertexSE3Expmap”。
• 误差项为一个像素的测量误差。由于整个优化过程中$\mathbf{I}_1(\mathbf{p}_1)$保持不变，我们可以把它当成一个固定的预设值，从而调整相机位姿，使$\mathbf{I}_2(\mathbf{p}_2)$接近这个值。于是，这种边只连接一个顶点，为 一元边。由于g2o中本身没有计算测量误差的边，我们需要自己定义一种新的边。

　　整个直接法图优化问题是由一个相机位姿顶点与许多条一元边组成。如果使用稀疏的直接法，那我们大约会有几百至几千条这样的边；稠密直接法则会有几十万条边。优化问题对应的线性方程是计算李代数增量（6$\times$1），本身规模不大，所以主要的计算时间会花费在每条边的误差与雅可比的计算上。下面的实验中，我们先来定义一种专门用于计算直接法的边，然后，使用该边构建图优化问题并求解之。

实验工程位于：https://github.com/gaoxiang12/slambook 中的 ch8/directMethod中。

　　工程目录下的g2o\_types.h中给出了自定义边的声明，g2o\_types.cpp中给出实现，我们在CMakeLists.txt里将它们编译了成一个库。

#ifndef G2O_TYPES_DIRECT_H_
#define G2O_TYPES_DIRECT_H_

// 定义应用于直接法的g2o边
#include <Eigen/Geometry>
#include <g2o/core/base_unary_edge.h>
#include <g2o/types/sba/types_six_dof_expmap.h>
#include <opencv2/core/core.hpp>
namespace g2o
{
// project a 3d point into an image plane, the error is photometric error 
// an unary edge with one vertex SE3Expmap (the pose of camera)
class EdgeSE3ProjectDirect: public BaseUnaryEdge< 1, double, VertexSE3Expmap>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    
    EdgeSE3ProjectDirect() {}
    
    EdgeSE3ProjectDirect( Eigen::Vector3d point, float fx, float fy, float cx, float cy, cv::Mat* image )
    : x_world_(point), fx_(fx), fy_(fy), cx_(cx), cy_(cy), image_(image)
    {}
    
    virtual void computeError(); 
    
    // plus in manifold 
    virtual void linearizeOplus( ); 
    
    // dummy read and write functions because we don't care... 
    virtual bool read( std::istream& in );
    virtual bool write( std::ostream& out ) const ;
    
protected:
    float getPixelValue( float x, float y ); 
public:
    // 3d point in world frame 
    Eigen::Vector3d x_world_; 
    // Pinhole camera intrinsics 
    float cx_=0, cy_=0, fx_=0, fy_=0; 
    // the reference image 
    cv::Mat* image_=nullptr;
};
} // namespace g2o 
#endif // G@O_TYPES_DIRECT_H_

 　　我们的边继承自g2o::BaseUnaryEdge。在继承时，需要在模板参数里填入测量值的维度、类型，以及连接此边的顶点，同时，我们把空间点$P$、相机内参和图像存储在该边的成员变量中。为了让g2o优化该边对应的误差，我们需要覆写两个虚函数：用computeError()计算误差值，用linearizeOplus()计算雅可比。其余的存储和读取函数，由于本次实验不关心，就略去了。下面我们给出这两个函数的实现：

#include "g2o_types.h"
#include <g2o/core/factory.h>

#include <iostream>

using namespace std; 

namespace g2o
{
    
G2O_REGISTER_TYPE(EDGE_PROJECT_SE3_DIRECT, EdgeSE3ProjectDirect );

// compute the photometric error
void EdgeSE3ProjectDirect::computeError()
{
    const VertexSE3Expmap* v  =static_cast<const VertexSE3Expmap*> ( _vertices[0] );
    Eigen::Vector3d x_local = v->estimate().map ( x_world_ );
    float x = x_local[0]*fx_/x_local[2] + cx_;
    float y = x_local[1]*fy_/x_local[2] + cy_;
    // check x,y is in the image
    if ( x-4<0 || ( x+4 ) >image_->cols || ( y-4 ) <0 || ( y+4 ) >image_->rows )
        _error(0,0) = 999.0;
    else
    {
        _error(0,0) = getPixelValue(x,y) - _measurement;
    }
}

// the bilinear interpolated pixel value
float EdgeSE3ProjectDirect::getPixelValue ( float x, float y )
{
    uchar* data = & image_->data[ int(y) * image_->step + int(x) ];
    float xx = x - floor ( x );
    float yy = y - floor ( y );
    float v = (
                 ( 1-xx ) * ( 1-yy ) * data[0] +
                 xx* ( 1-yy ) * data[1] +
                 ( 1-xx ) *yy*data[ image_->step ] +
                 xx*yy*data[image_->step+1]
             );
    return v;
}

// plus in manifold
void EdgeSE3ProjectDirect::linearizeOplus()
{
    VertexSE3Expmap* vtx = static_cast<VertexSE3Expmap*> ( _vertices[0] );

    Eigen::Vector3d xyz_trans = vtx->estimate().map ( x_world_ );

    double x = xyz_trans[0];
    double y = xyz_trans[1];
    double invz = 1.0/xyz_trans[2];
    double invz_2 = invz*invz;

    float u = x*fx_*invz + cx_;
    float v = y*fy_*invz + cy_;
    
    // jacobian from se3 to u,v
    // note that in g2o the Lie algebra is (\omega, \epsilon), where \omega is so(3) and \epsilon the translation
    Eigen::Matrix<double, 2, 6> jacobian_uv_ksai;

    jacobian_uv_ksai ( 0,0 ) = - x*y*invz_2 *fx_;
    jacobian_uv_ksai ( 0,1 ) = ( 1+ ( x*x*invz_2 ) ) *fx_;
    jacobian_uv_ksai ( 0,2 ) = - y*invz *fx_;
    jacobian_uv_ksai ( 0,3 ) = invz *fx_;
    jacobian_uv_ksai ( 0,4 ) = 0;
    jacobian_uv_ksai ( 0,5 ) = -x*invz_2 *fx_;

    jacobian_uv_ksai ( 1,0 ) = -( 1+y*y*invz_2 ) *fy_;
    jacobian_uv_ksai ( 1,1 ) = x*y*invz_2 *fy_;
    jacobian_uv_ksai ( 1,2 ) = x*invz *fy_;
    jacobian_uv_ksai ( 1,3 ) = 0;
    jacobian_uv_ksai ( 1,4 ) = invz *fy_;
    jacobian_uv_ksai ( 1,5 ) = -y*invz_2 *fy_;

    Eigen::Matrix<double, 1, 2> jacobian_pixel_uv;
    
    jacobian_pixel_uv ( 0,0 ) = ( getPixelValue(u+1,v)-getPixelValue(u,v) );
    jacobian_pixel_uv ( 0,1 ) = ( getPixelValue(u,v+1)-getPixelValue(u,v) );
    
    _jacobianOplusXi = jacobian_pixel_uv*jacobian_uv_ksai;
}
bool EdgeSE3ProjectDirect::read( std::istream& in )
{
    return true;
}

bool EdgeSE3ProjectDirect::write( std::ostream& out ) const
{
    return true;
}


}// namespace g2o

 　　可以看到，这里的雅可比计算与式（\ref{eq:jacobianofDirect}）是一致的。注意我们在程序中的误差计算里，使用了$\mathbf{I}_2(\mathbf{p}_2) - \mathbf{I}_1(\mathbf{p}_1)$的形式，因此前面的负号可以省去，只需把像素梯度乘以像素到李代数的梯度即可。

　　在程序中，相机位姿是用浮点数表示的，投影到像素坐标也是浮点形式。为了更精细地计算像素亮度，我们要对图像进行插值。我们这里采用了简单的双线性插值，您也可以使用更复杂的插值方式，但计算代价可能会变高一些。

---

 5. 使用直接法估计相机运动

　　定义了g2o边后，我们将节点和边组合成图，就可以调用g2o进行优化了。实现代码位于 slambook/ch8/directMethod/direct\_sparse.cpp中，请读者阅读该部分代码并编译它。我们将代码编译的步骤留作习题吧（一脸贱笑中）。

#include <iostream>
#include <fstream>
#include <list>
#include <vector>
#include <chrono>
#include <ctime>
#include <climits>

#include <opencv2/core/core.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/features2d/features2d.hpp>

#include "g2o_types.h"
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <g2o/core/robust_kernel.h>
#include <g2o/types/sba/types_six_dof_expmap.h>

using namespace std;

// 一次测量的值，包括一个世界坐标系下三维点与一个灰度值
struct Measurement
{
    Measurement( Eigen::Vector3d p, float g ): pos_world(p), grayscale(g) {}
    Eigen::Vector3d pos_world;
    float grayscale;
};

inline Eigen::Vector3d project2Dto3D ( int x, int y, int d, float fx, float fy, float cx, float cy, float scale )
{
    float zz = float ( d ) /scale;
    float xx = zz* ( x-cx ) /fx;
    float yy = zz* ( y-cy ) /fy;
    return Eigen::Vector3d ( xx, yy, zz );
}

inline Eigen::Vector2d project3Dto2D( float x, float y, float z, float fx, float fy, float cx, float cy )
{
    float u = fx*x/z+cx;
    float v = fy*y/z+cy;
    return Eigen::Vector2d(u,v);
}

// 直接法估计位姿
// 输入：测量值（空间点的灰度），新的灰度图，相机内参； 输出：相机位姿
// 返回：true为成功，false失败
bool poseEstimationDirect( const vector<Measurement>& measurements, cv::Mat* gray, Eigen::Matrix3f& intrinsics, Eigen::Isometry3d& Tcw );

int main ( int argc, char** argv )
{
    if ( argc != 2 )
    {
        cout<<"usage: useLK path_to_dataset"<<endl;
        return 1;
    }
    srand( (unsigned int) time(0) );
    string path_to_dataset = argv[1];
    string associate_file = path_to_dataset + "/associate.txt";

    ifstream fin ( associate_file );

    string rgb_file, depth_file, time_rgb, time_depth;
    cv::Mat color, depth, gray;
    vector<Measurement> measurements;
    // 相机内参
    float cx = 325.5;
    float cy = 253.5;
    float fx = 518.0;
    float fy = 519.0;
    float depth_scale = 1000.0;
    Eigen::Matrix3f K;
    K<<fx,0.f,cx,0.f,fy,cy,0.f,0.f,1.0f;

    Eigen::Isometry3d Tcw = Eigen::Isometry3d::Identity(); 

    cv::Mat prev_color;
    //  我们演示两个图像间的直接法计算
    for ( int index=0; index<2; index++ )
    {
        cout<<"*********** loop "<<index<<" ************"<<endl;
        fin>>time_rgb>>rgb_file>>time_depth>>depth_file;
        color = cv::imread ( path_to_dataset+"/"+rgb_file );
        depth = cv::imread ( path_to_dataset+"/"+depth_file, -1 );
        cv::cvtColor ( color, gray, cv::COLOR_BGR2GRAY );
        if ( index ==0 )
        {
            // 对第一帧提取FAST特征点
            vector<cv::KeyPoint> keypoints;
            cv::Ptr<cv::FastFeatureDetector> detector = cv::FastFeatureDetector::create();
            detector->detect ( color, keypoints );
            for ( auto kp:keypoints )
            {
                // 去掉邻近边缘处的点
                if ( kp.pt.x < 20 || kp.pt.y < 20 || (kp.pt.x+20)>color.cols || (kp.pt.y+20)>color.rows )
                    continue;
                ushort d = depth.ptr<ushort> ( int( kp.pt.y ) ) [ int(kp.pt.x) ];
                if ( d==0 )
                    continue;
                Eigen::Vector3d p3d = project2Dto3D ( kp.pt.x, kp.pt.y, d, fx, fy, cx, cy, depth_scale );
                float grayscale = float ( gray.ptr<uchar> ( int(kp.pt.y) ) [ int(kp.pt.x) ] );
                measurements.push_back ( Measurement( p3d, grayscale ) );
            }
            prev_color = color.clone();
            continue;
        }
        // 使用直接法计算相机运动及投影点
        chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
        poseEstimationDirect( measurements, &gray, K, Tcw );
        chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
        chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>( t2-t1 );
        cout<<"direct method costs time: "<<time_used.count()<<" seconds."<<endl;
        cout<<"Tcw="<<Tcw.matrix()<<endl;
        
        // plot the feature points 
        cv::Mat img_show( color.rows, color.cols*2, CV_8UC3 );
        prev_color.copyTo( img_show( cv::Rect(0,0,color.cols, color.rows) ) );
        color.copyTo( img_show(cv::Rect(color.cols,0,color.cols, color.rows)) );
        for ( Measurement m:measurements )
        {
            Eigen::Vector3d p = m.pos_world;
            Eigen::Vector2d pixel_prev = project3Dto2D( p(0,0), p(1,0), p(2,0), fx, fy, cx, cy );
            Eigen::Vector3d p2 = Tcw*m.pos_world;
            Eigen::Vector2d pixel_now = project3Dto2D( p2(0,0), p2(1,0), p2(2,0), fx, fy, cx, cy );
            
            float b = 255*float(rand())/RAND_MAX;
            float g = 255*float(rand())/RAND_MAX;
            float r = 255*float(rand())/RAND_MAX;
            cv::circle(img_show, cv::Point2d(pixel_prev(0,0), pixel_prev(1,0)), 5, cv::Scalar(b,g,r),1 );
            cv::circle(img_show, cv::Point2d(pixel_now(0,0)+color.cols, pixel_now(1,0)), 5, cv::Scalar(b,g,r),1 );
            cv::line( img_show, cv::Point2d(pixel_prev(0,0), pixel_prev(1,0)), cv::Point2d(pixel_now(0,0)+color.cols, pixel_now(1,0)), cv::Scalar(b,g,r), 1 );
        }
        cv::imshow( "result", img_show );
        cv::waitKey(0);
        
    }
    return 0;
}

bool poseEstimationDirect ( const vector< Measurement >& measurements, cv::Mat* gray, Eigen::Matrix3f& K, Eigen::Isometry3d& Tcw )
{
    // 初始化g2o
    typedef g2o::BlockSolver<g2o::BlockSolverTraits<6,1>> DirectBlock;  // 求解的向量是6＊1的
    DirectBlock::LinearSolverType* linearSolver = new g2o::LinearSolverDense< DirectBlock::PoseMatrixType > ();
    DirectBlock* solver_ptr = new DirectBlock( linearSolver );
    g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
    g2o::SparseOptimizer optimizer; 
    optimizer.setAlgorithm( solver );
    optimizer.setVerbose( true );       // 打开调试输出
    
    g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); 
    pose->setEstimate( g2o::SE3Quat(Tcw.rotation(), Tcw.translation()) );
    pose->setId(0);
    optimizer.addVertex( pose );
    
    // 添加边
    int id=1;
    for( Measurement m: measurements )
    {
        g2o::EdgeSE3ProjectDirect* edge = new g2o::EdgeSE3ProjectDirect(
            m.pos_world,
            K(0,0), K(1,1), K(0,2), K(1,2), gray
        );
        edge->setVertex( 0, pose );
        edge->setMeasurement( m.grayscale );
        edge->setInformation( Eigen::Matrix<double,1,1>::Identity() );
        edge->setId( id++ );
        optimizer.addEdge(edge);
    }
    cout<<"edges in graph: "<<optimizer.edges().size()<<endl;
    optimizer.initializeOptimization();
    optimizer.optimize(10);
    Tcw = pose->estimate();
}

 　　在这个实验中，我们读取TUM数据集的两对RGB-D图像。然后，对第一张图像提取FAST关键点（不需要描述子），并使用直接法估计这些关键点在第二个图像中的位置，以及第二个图像的相机位姿。这就构成了一种简单的稀疏直接法。最后，我们画出这些关键点在第二个图像中的投影。运行

build/direct_sparse ~/dataset/rgbd_dataset_freiburg1_desk

 　　程序会在作图之后暂停，您可以特征点的位置关系，也可以看到迭代误差的下降过程。图：稀疏直接法的实验。左：误差随着迭代下降。右：参考帧与后1至3帧对比（选取部分关键点）。

---

 6. 直接法的讨论

　　相比于特征点法，直接法完全依靠像优化来求解相机位姿。从式（\ref{eq:jacobianofDirect}）中可以看到，像素梯度引导着优化的方向。如果我们想要得到正确的优化结果，就必须保证大部分像素梯度能够把优化引导到正确的方向。

　　这是什么意思呢？我们希望更深入地理解直接法的做法。现在，我们来扮演一下优化算法。假设对于参考图像，我们测量到一个灰度值为229的像素。并且，由于我们知道它的深度，可以推断出空间点$P$的位置。

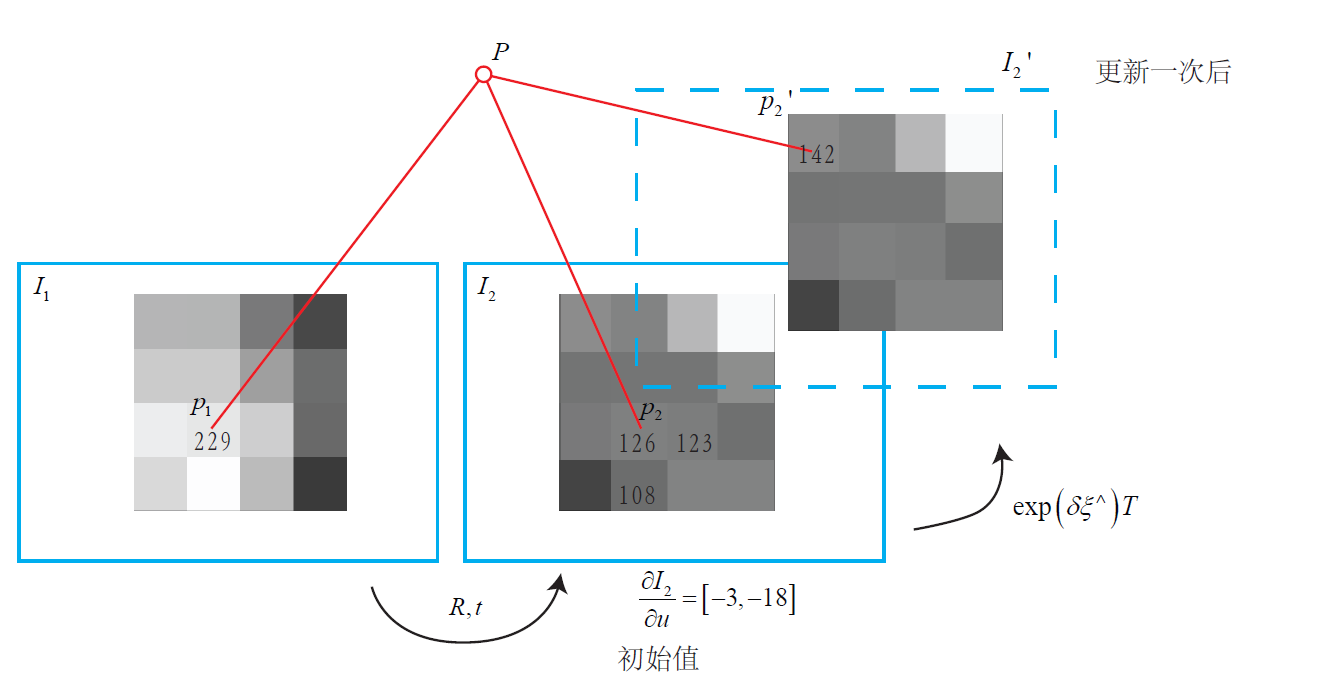
　　此时我们又得到了一张新的图像，需要估计它的相机位姿。这个位姿是由一个初值再上不断地优化迭代得到的。假设我们的初值比较差，在这个初值下，空间点$P$投影后的像素灰度值是126。于是，这个像素的误差为$229-126=103$，我们希望微调相机的位姿，使像素更亮一些。
　　怎么知道往哪里微调，像素会更亮呢？这就需要用到像素梯度。我们在图像中发现，沿$u$轴往前走一步，该处的灰度值变成了123，即减去了3。同样地，沿$v$轴往前走一步，灰度值减18，变成108。在这个像素周围，我们看到梯度是$[-3,-18]$，为了提高亮度，我们会建议优化算法微调相机，使$P$的像往左上方移动。由于这个梯度是在局部求解的，这个移动量不能太大。
　　但是，优化算法不能只听这个像素的一面之词，还需要听取其他像素的建议。综合听取了许多像素的意见之后，优化算法选择了一个和我们建议的方向偏离不远的地方，计算出一个更新量$\exp ({\mathbf{\xi}^\wedge } )$。加上更新量后，图像从$I_2$移动到了$I_2'$，像素的投影位置也变到了一个更亮的地方。我们看到，通过这次更新，误差变小了。在理想情况下，我们期望误差会不断下降，最后收敛。

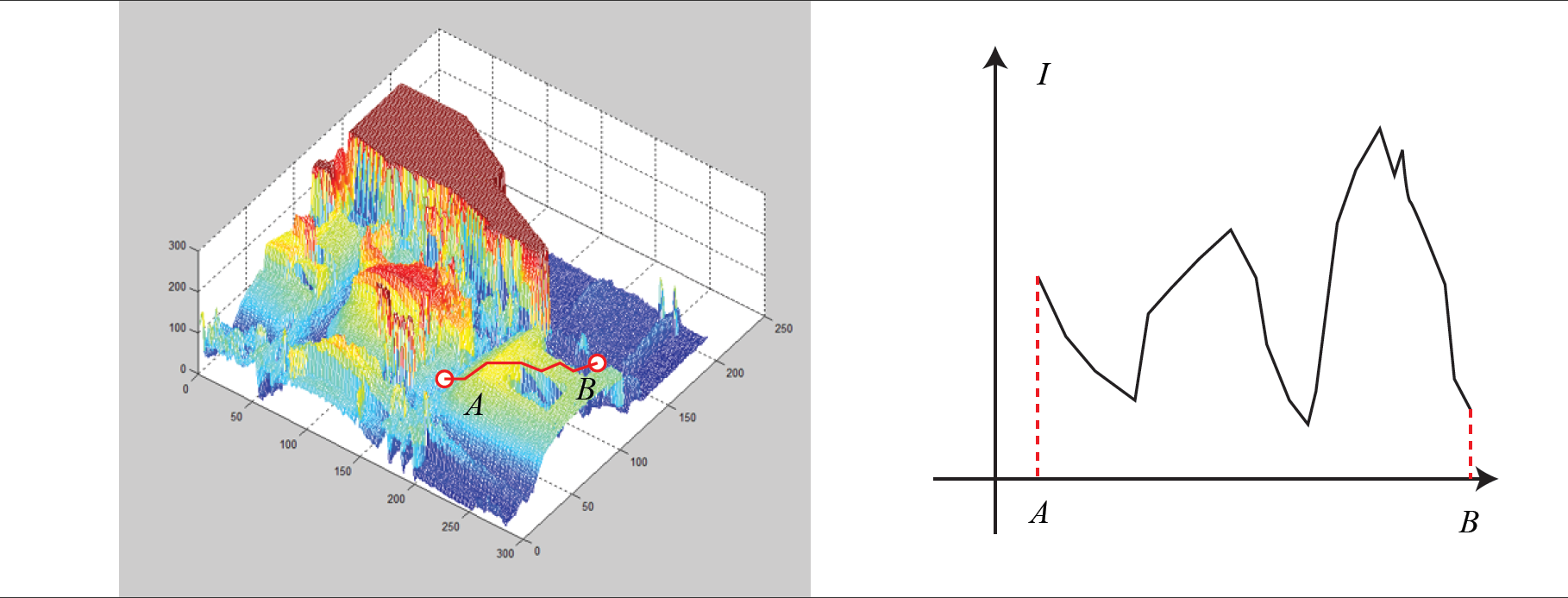
　　但是实际是不是这样呢？我们是否真的只要沿着梯度方向走，就能走到一个最优值？注意到，直接法的梯度是直接由图像梯度确定的，因此我们必须保证沿着图像梯度走时，灰度误差会不断下降。然而，图像通常是一个很强烈的非凸函数，如下图所示。实际当中，如果我们沿着图像梯度前进，很容易由于图像本身的非凸性（或噪声）落进一个局部极小值中，无法继续优化。只有当相机运动很小，图像中的梯度不会有很强的非凸性时，直接法才能成立。

　　在例程中，我们只计算了单个像素的差异，并且这个差异是由灰度直接相减得到的。然而，单个像素没有什么区分性，周围很可能有好多像素和它的亮度差不多。所以，我们有时会使用小的图像块（patch），并且使用更复杂的差异度量方式，例如归一化相关性（Normalized Cross Correlation，NCC）等。而例程为了简单起见，使用了误差的平方和，以保持和推导的一致性。

---

 7. 直接法的优缺点总结

　　最后，我们总结一下直接法的优缺点。大体来说，它的优点如下：

• 可以省去计算特征点、描述子的时间。
• 只要求有像素梯度即可，无须特征点。因此，直接法可以在特征缺失的场合下使用。比较极端的例子是只有渐变的一张图像。它可能无法提取角点类特征，但可以用直接法估计它的运动。
• 可以构建半稠密乃至稠密的地图，这是特征点法无法做到的。

　　另一方面，它的缺点也很明显：

• 非凸性——直接法完全依靠梯度搜索，降低目标函数来计算相机位姿。其目标函数中需要取像素点的灰度值，而图像是强烈非凸的函数。这使得优化算法容易进入极小，只在运动很小时直接法才能成功。
• 单个像素没有区分度。找一个和他像的实在太多了！——于是我们要么计算图像块，要么计算复杂的相关性。由于每个像素对改变相机运动的“意见”不一致。只能少数服从多数，以数量代替质量。
• 灰度值不变是很强的假设。如果相机是自动曝光的，当它调整曝光参数时，会使得图像整体变亮或变暗。光照变化时亦会出现这种情况。特征点法对光照具有一定的容忍性，而直接法由于计算灰度间的差异，整体灰度变化会破坏灰度不变假设，使算法失败。

　　直接法就是这样一种优缺点都非常明显的方法，你有没有爱上它呢？