Attention 机制
有一篇paper叫做attention is all your need,好霸气的名字。。不过它值得,哈哈,但是我现在不打算解析paper
一开始以为是attention不理解,其实是seq-seq的encoder和decoder部分没搞明白,感觉现在差不多了,可以自己复述了。
Attention
注意力机制就是为了解决当解码的序列太长时,越到后面效果就越差。因为在未引入注意力机制之前,解码时仅仅只依靠上一时刻的输出而忽略的编码阶段每个时刻的输出(“称之为记忆”)。注意力机制的思想在于,希望在解码的时刻能够参考编码阶段的记忆,对上一时刻输出的信息做一定的处理(也就是只注意其中某一部分),然后再喂给下一时刻做解码处理。这样就达到了解码当前时刻时,仅仅只接受与当前时刻有关的输入,类似与先对信息做了一个筛选(注意力选择)。Encoder 把所有的输入序列编码成了一个c向量,然后使用c向量来进行解码,因此, 向量中必须包含了原始序列中的所有信息,所以它的压力其实是很大的,而且由于 RNN 容易把前面的信息“忘记”掉,所以基本的 Seq2Seq 模型,对于较短的输入来说,效果还是可以接受的,但是在输入序列比较长的时候, 向量存不下那么多信息,就会导致生成效果大大折扣。
解码的时候参考编码阶段的记忆,对于encoder输出的信息做一定的筛选,保留重要的一部分,前筛。。
既然一个上下文\(c\)向量存不了,那么就引入多个\(c\)向量,称之为\(c_1\) 、\(c_2\)、…、\(c_i\),在解码的时候,这里的\(c_i\)对应着Decoder的解码位次,每次解码就利用对应的\(c_i\)向量来解码.这里的每个\(c_i\)向量其实包含了当前所输出与输入序列各个部分重要性的相关的信息。
还是需要借助大神的一张清晰的图
这个是一个seq-seq模型的翻译demo
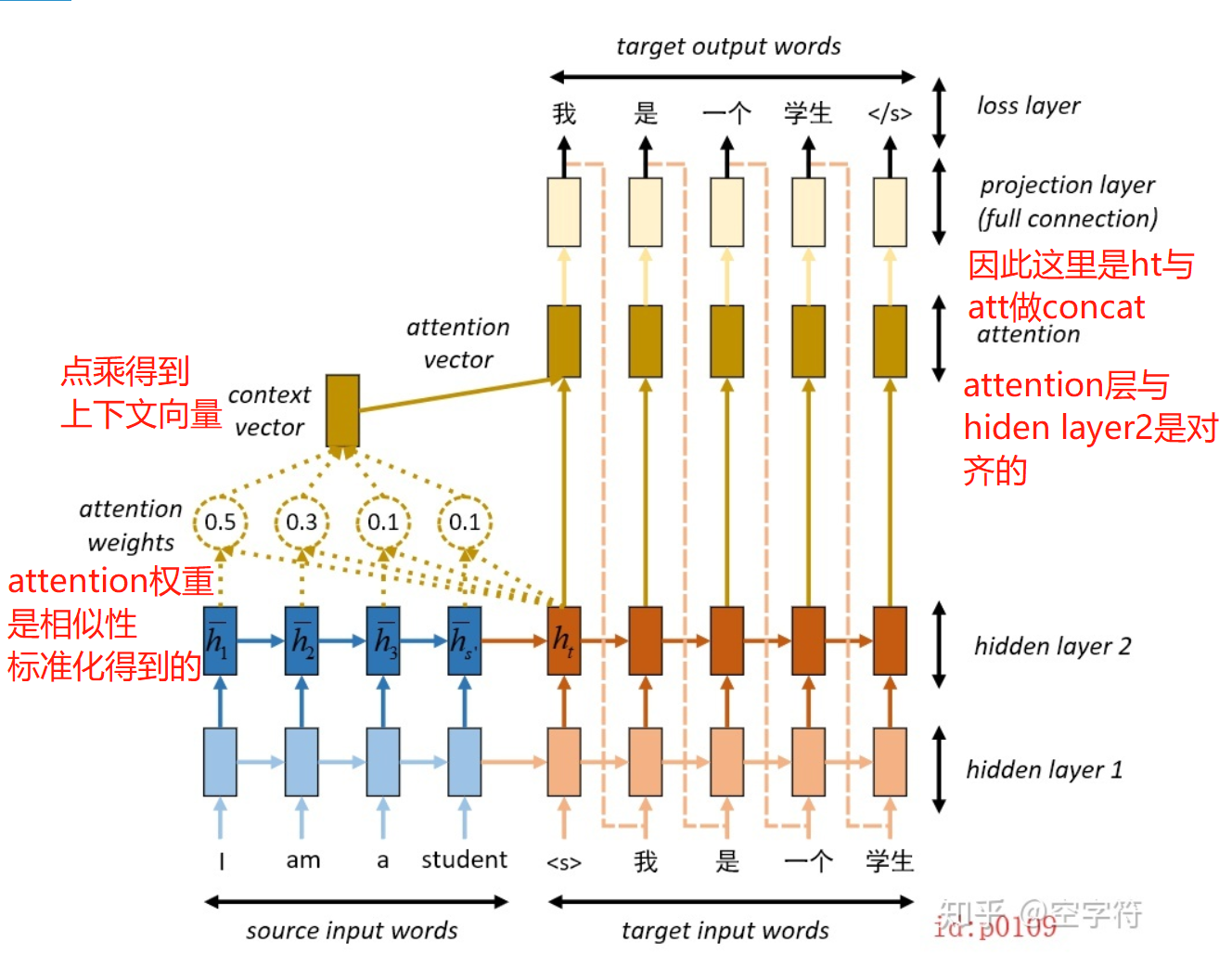
上图右边的输入部分的实线表示是训练时的输入,虚线表示预测时的输入。注意向量(attention vector)是由解码部分每个时刻的计算产生的,此处以计算第一个时刻为例。
encoder-decoder
英文句子“I am a student”被输入到一个两个的LSTM编码网络(蓝色部分),经过编码(encoder)后输入到另外一个两层的LSTM解码网络(棕色部分)。当网络在按时刻进行翻译decoder
(解码)的时候,第一个时刻输出的就是图中的 \(h_t\)。在前面我们说到,我们希望网络也能同我们人脑的思考过程一样,在依次翻译每个时刻时,网络所“联想”到的都是与当前时刻最相关(相似)的映射。换句话说,在神经网络将"I am a student"翻译成中文的过程中,当解码到第一个时刻时,我们希望网络仅仅只是将注意力集中到单词"I"上,而尽可能忽略其它单词的影响。可这说起来容易,具体该怎么做,怎么体现呢?
\(\overline{h_{1}}\)是encoder部分的hiden layer
我们知道 \(h_t\) 是第一个解码时刻的隐含状态,同时以上帝视角来看,最与 \(h_t\)相关的部分应该是"I"对应的编码状态 \(\overline{h_{1}}\) 。因此,只要网络在解码第一个时刻时,将注意力主要集中于 \(\overline{h_{1}}\),也就算达成目的了。但我们怎么才能让解码部分的网络也能知道这一事实呢?好在此时的 \(h_t\) 与编码部分的隐含状态都处于同一个Embedding space,所以我们可以通过相似度对比来告诉解码网络:哪个编码时刻的隐含状态与当前解码时刻的隐含状态最为相似。这样,在解码当前时刻时,网络就能将“注意力”尽可能多的集中于对应编码时刻的隐含状态。
简单的来说做下encoder与decoder的相似度
相似度得分有两种计算方式
\(\operatorname{score}\left(h_{t}, \bar{h}_{s}\right)=\left\{\begin{array}{ll}h_{t}^{T} W \bar{h}_{s}, & \text { [Luong's multiplicative style } ] \\ v^{T} \tanh \left(w_{1} h_{t}+w_{2} \bar{h}_{s}\right), & \text { [Bahdanau's additive style] }\end{array}\right.\)
把相似度得分进行标准化也就是使用softmax,就会得到一个0-1之间的值,找个值就是对应的attention的权重
\(\alpha_{t s}=\frac{\exp \left(\operatorname{score}\left(h_{t}, \bar{h} s\right)\right)}{\sum s^{\prime}=1^{S} \exp \left(s \operatorname{core}\left(h_{t}, \bar{h} s^{\prime}\right)\right)}\)
[Attention weights]
当网络分别得到当前解码时刻与所有编码时刻对应的相似度系数之后(图中的attention weights),再以加权就和的形式将所有的编码状态累加起来得到context vector,最终与 \(h_t\) 组合得到当前decoder解码时刻的输出。之所以要以加权求和的形式进行是因为,虽然此时的\(h_t\)仅仅只与 \(\overline{h_{1}}\)最为相关,但同样也受其它编码状态的影响(例如到句型复杂的时候)。但是,若是换了应用场景,只进行对应权重乘以对应隐含状态,不进行累加也是可以的。
context vector
也就是attention-weight与\(\overline{h_{1}}\)做mutmal矩阵相乘
\(c_{t}=\sum_{s} \alpha t s \bar{h}_{s} \quad[\text { Context vector }]\)
得到的att向量是context vector与decoder端的hiden layer :\(h_t\)做的concatenate
注意,attention vector与\(h_t\)是一一对应的关系,不然办法做concatenate。
\(c_{t}=\sum_{s} \alpha t s \bar{h}_{s} \quad[\text { Context vector }]\)
我觉得到这里attention机制如何工作以及怎样计算是ok的,attention就是一个找相似度的过程。但是如何得知将attention机制放到哪一层hiden layer呢?
因此,不知道放到哪个hiden layer:\(h_t\),创造一个hiden layer:\(h_t\)然后跟着网络一起训练,可以得到一个动态的weight
将 \(c_{t}\),\(h_t\)结合作为输出,也可以直接将 \(c_{t}\)作为输出,感觉前者的预测效果更好
concatenate的用法
import numpy as np
import keras.backend as K
import tensorflow as tf
a = K.variable(np.array([[[1, 2], [2, 3]], [[4, 4], [5, 3]]]))
b = K.variable(np.array([[[7, 4], [8, 4]], [[2, 10], [15, 11]]]))
c1 = K.concatenate([a, b], axis=0)
c2 = K.concatenate([a, b], axis=1)
c3 = K.concatenate([a, b], axis=2)
#试试默认的参数
c4 = K.concatenate([a, b])
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
print(sess.run(c1))
print()
print(sess.run(c2))
print()
print(sess.run(c3))
print()
print(sess.run(c4))
以上的axis=0表示列维,1表示行维,沿着通道维度连接两个张量。
输出的结果会是这样的:
[[[ 1. 2.]
[ 2. 3.]]
[[ 4. 4.]
[ 5. 3.]]
[[ 7. 4.]
[ 8. 4.]]
[[ 2. 10.]
[15. 11.]]]
[[[ 1. 2.]
[ 2. 3.]
[ 7. 4.]
[ 8. 4.]]
[[ 4. 4.]
[ 5. 3.]
[ 2. 10.]
[15. 11.]]]
[[[ 1. 2. 7. 4.]
[ 2. 3. 8. 4.]]
[[ 4. 4. 2. 10.]
[ 5. 3. 15. 11.]]]
[[[ 1. 2. 7. 4.]
[ 2. 3. 8. 4.]]
[[ 4. 4. 2. 10.]
[ 5. 3. 15. 11.]]]
另外,除联合维度之外其它维度都必须相等。
相似度度量
Q,K,V
解释一下attention中出现的这三个矩阵

