generalization error
泛化误差
机器学习中的Bias(偏差),Error(误差),和Variance(方差)有什么区别和联系?
准与确的关系
bias
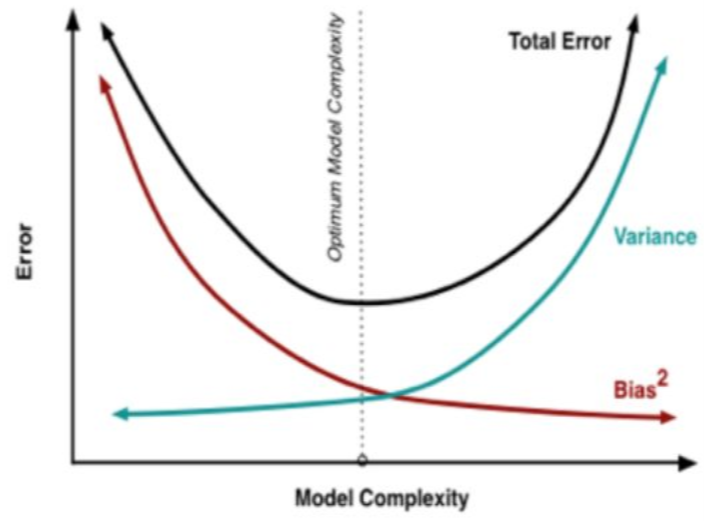
偏差:模型越复杂,模型的偏差越小,方差越小,因此会出现overfitting
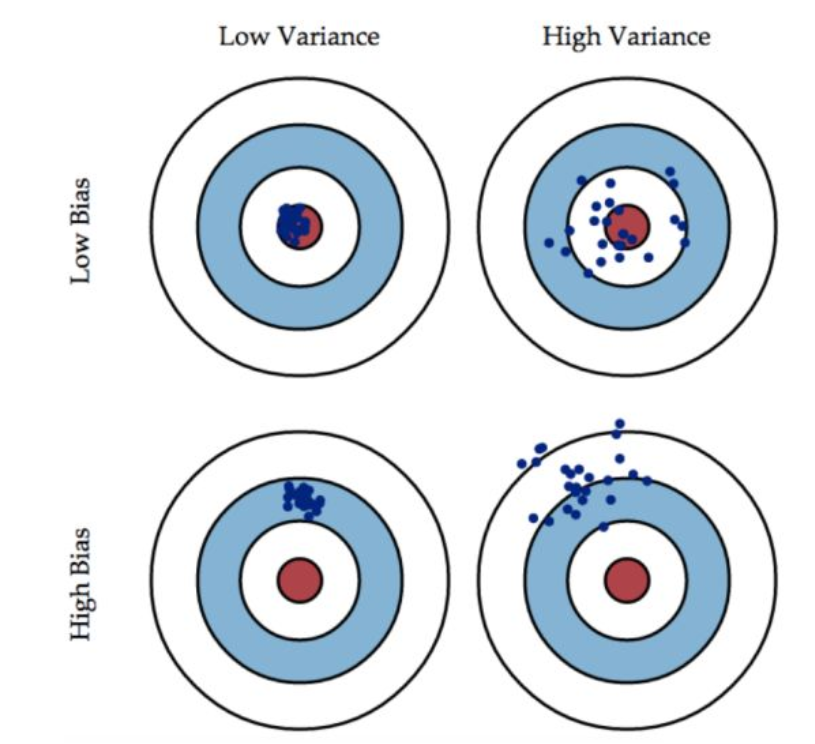
准:bias描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距:\(E|y_{真实}-y_{预测}|\),就是分类器在样本上(测试集)上拟合的好不好。因此想要降低bias,就要复杂化模型,增加模型的参数,容易导致过拟合,过拟合对应的是上面的high variance,点比较分散。low bias对应的就是点都打在靶心附近,所以描述的是准,但是不一定稳
variance
方差:模型越简单,模型的拟合度一般,模型方差越小,偏差越大,因此会出现underfitting
描述的是样本训练出来的模型在测试集上的表现,想要降低variance,就要简化模型,减少模型的复杂程度,这样比较容易欠拟合,low variance对应的就是点打的都很集中,但是不一定准
这个靶子上的点(hits)可以理解成一个个的拟合模型,如果许多个拟合模型都聚集在一堆,位置比较偏,如图中high bias ,low variance这种情景,意味着无论什么样子的数据灌进来,拟合的模型都差不多,这个模型过于简陋了,参数太少了,复杂度太低了,这就是欠拟合:但如果是图中low bias, high variance这种情景,你看,所有拟合模型都围绕中间那个correct target均匀分布,但又不够集中,很散,这就意味着,灌进来的数据一有风吹草动,拟合模型就跟着剧烈变化,这说明这个拟合模型过于复杂了,不具有普适性,就是过拟合。
所以bias和variance的选择是一个tradeoff(取舍思维),过高的varance对应的概念,有点「剑走偏锋」[矫枉过正」的意思,如果说一个人variance比较高, 可以理解为,这个人性格比较极端偏执,眼光比较狭窄,没有大局观。而过高的bias对应的概念,有点像「面面俱到」「大巧若拙] 的意思,如果说一个人bias比较高,可以理解为,这个人是个好好先生,谁都不得罪, 圆滑世故,说话的时候,什么都说了,但又好像什么都没说,眼光比较长远,有大局观。(感觉好分裂 ),或许可以说泛化能力更强,谁都适用,就是没啥用。

总结
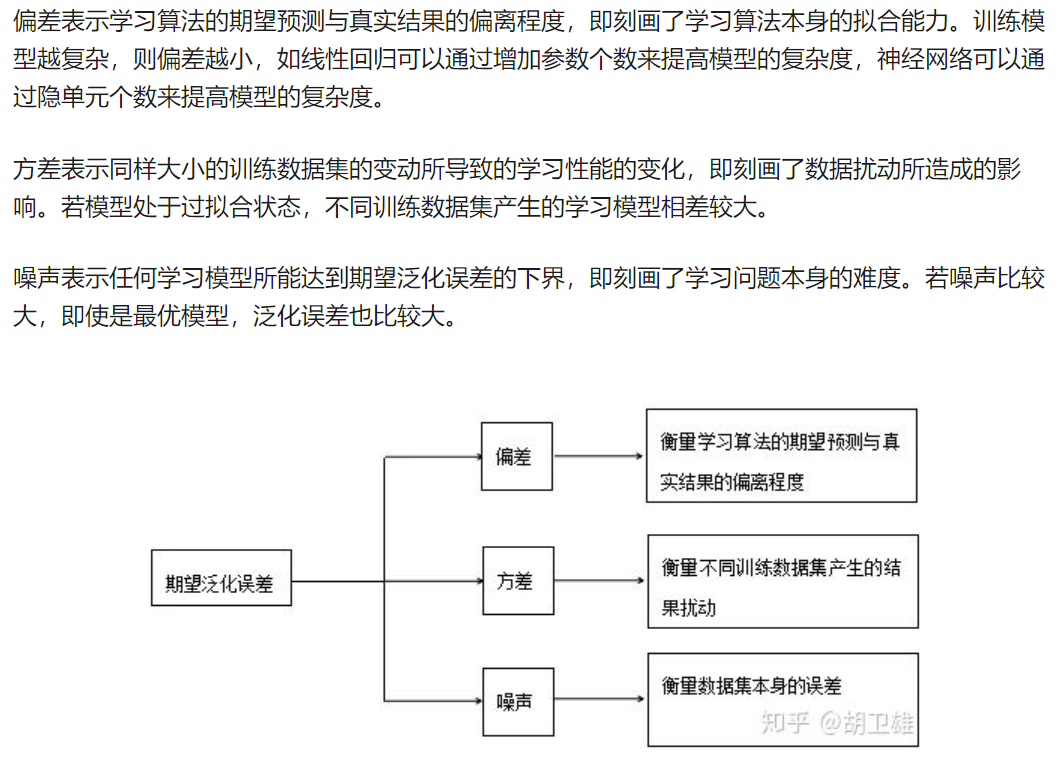
偏差度量了学习算法的期望预测与真实结果的偏离程度,即刻画了算法本身的拟合能力;
方差度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响;
噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了学习问题的本身难度
偏差-方差分解说明,泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定的学习任务,为了取得好的泛化性能,则需使偏差较小,即能够充分拟合数据,并且使方差较小,即使数据扰动产生的影响小。一般来说方差与偏差是有冲突的,这称为方差-偏差窘境csdn
error
Error反映的是整个模型的准确度,说白了就是你给出的模型,input一个变量,和理想的output之间吻合程度,吻合度高就是Error低。Bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度
\(error=bias+variance+噪声\)
Error反映的是整个模型的准确度,Bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度,Variance反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性
在一个实际系统中,Bias与Variance往往是不能兼得的。如果要降低模型的Bias,就一定程度上会提高模型的Variance,反之亦然。造成这种现象的根本原因是,我们总是希望试图用有限训练样本去估计无限的真实数据。当我们更加相信这些数据的真实性,而忽视对模型的先验知识,就会尽量保证模型在训练样本上的准确度,这样可以减少模型的Bias。但是,这样学习到的模型,很可能会失去一定的泛化能力,从而造成过拟合,降低模型在真实数据上的表现,增加模型的不确定性。相反,如果更加相信我们对于模型的先验知识,在学习模型的过程中对模型增加更多的限制,就可以降低模型的variance,提高模型的稳定性,但也会使模型的Bias增大。
Bias与Variance两者之间的trade-off是机器学习的基本主题之一,机会可以在各种机器模型中发现它的影子。具体到K-fold Cross Validation的场景,其实是很好的理解的。首先看Variance的变化,还是举打靶的例子。假设我把抢瞄准在10环,虽然每一次射击都有偏差,但是这个偏差的方向是随机的,也就是有可能向上,也有可能向下。那么试验次数越多,应该上下的次数越接近,那么我们把所有射击的目标取一个平均值,也应该离中心更加接近。更加微观的分析,模型的预测值与期望产生较大偏差,
在模型固定的情况下,原因还是出在数据上,比如说产生了某一些异常点。在最极端情况下,我们假设只有一个点是异常的,如果只训练一个模型,那么这个点会对整个模型带来影响,使得学习出的模型具有很大的variance。但是如果采用k-fold Cross Validation进行训练,只有1个模型会受到这个异常数据的影响,而其余k-1个模型都是正常的。在平均之后,这个异常数据的影响就大大减少了。相比之下,模型的bias是可以直接建模的,只需要保证模型在训练样本上训练误差最小就可以保证bias比较小,而要达到这个目的,就必须是用所有数据一起训练,才能达到模型的最优解。因此,k-fold Cross Validation的目标函数破坏了前面的情形,所以模型的Bias必然要会增大。
如何处理 variance 较大的问题
减少特征数量
使用更简单的模型
增大你的训练数据集
使用正则化
加入随机因子,例如采用 bagging 和 boosting 方法
如何处理 bias 较大的问题
增加特征数量
使用更复杂的模型
去掉正则化jianshu