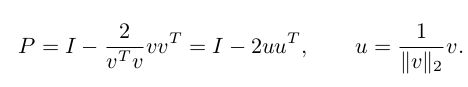机器学习中的矩阵方法02:正交
机器学习中的矩阵方法02:正交
说明:Matrix Methods in Data Mining and Pattern Recognition 读书笔记
1. 正交的一些概念和性质
在前一章的最小二乘的问题中,我们知道不恰当的基向量会出现条件数过大,系统防干扰能力差的现象,这实际上和基向量的正交性有关。
两个向量的内积如果是零, 那么就说这两个向量是正交的,在三维空间中,正交的两个向量相互垂直。如果相互正交的向量长度均为 1, 那么他们又叫做标准正交基。
正交矩阵则是指列向量相互正交的方阵。标准正交矩阵有具有如下性质:
-
-
若 P 和 Q 是标准正交矩阵,那么 X = PQ 也是标准正交矩阵。
-
正交矩阵最重要的性质之一是它的变换可以保证一个向量的长度不变,包括 Euclidean lenght , matrix norm 和 Frobenius norm.
2. 正交矩阵
在之前 coding the matrix 系列博客的第一篇我们知道,在复平面内,将一个向量逆时针旋转 度角度,只需要在该复数前面乘以
即可,现在我们要顺时针旋转,利用欧拉公式:
假设现在有一个复数: a + i b
左乘上面公式得到:
上述运算写成矩阵相乘的形式即为:

其中,左边的平面旋转矩阵就是一个标准的正交方阵,可以保证旋转后的向量与原来的向量长度相同。
有了 Givens 旋转方法,只要确定两个坐标之间的夹角,我们可以将任意向量旋转到单位向量 e1 上,过程如下:

用公式可以表示为:

有性质2推导出这个变换矩阵也是一个标准正交矩阵。
所以,向量长度不变:

3. Householder Transformations
现在手头有某一个向量 x, 想通过一个标准正交矩阵 P 将 x 转换为 y,有什么方法可以求出矩阵 P?一种方法是通过上面的旋转一步一步完成,P = G1G2G3。这里,我们有一个更加快捷的公式,即为 Householder Transformations.
拿上一小节的例子,求转换矩阵 P 的运算过程如下:
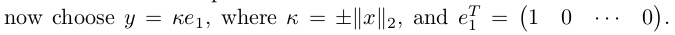 ,
,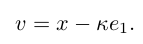 ,
,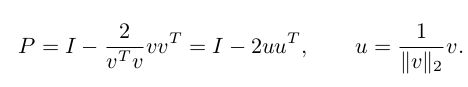
运算很简单,可以用笔验证上述过程是否正确。
用维基百科里面的一个图可以将上述运算过程表示成:

The goal is to find a linear transformation that changes the vector into a vector of same length which is collinear to . We could use an orthogonal projection (Gram-Schmidt) but this will be numerically unstable if the vectors and are close to orthogonal. Instead, the Householder reflection reflects through the dotted line (chosen to bisect the angle between and ). The maximum angle with this transform is at most 45 degrees.



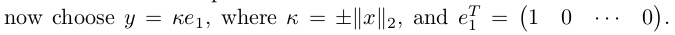 ,
,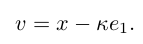 ,
,