线性回归——最小二乘法_实例(一)
上篇文章介绍了最小二乘法的理论与证明、计算过程,这里给出两个最小二乘法的计算程序代码;
Octave代码
clear all;close all;
% 拟合的数据集
x = [2;6;9;13];
y = [4;8;12;21];
% 数据长度
N = length(x); % 3
%% 计算x平均值
m_x = sum(x)/N;
%%
% 计算t的平均值
m_t = sum(y)/N;
%%
% 计算t*x的平均值
m_xt = sum(y.*x)/N;
%%
% 计算x平方的平均值
m_xx = sum(x.*x)/N;
%% 根据公式计算出f(x;m,c)=mx+c中m的值
w_1 = (m_xt - m_x*m_t)/(m_xx - m_x^2);
%% 计算出f(x;m,c)=mx+c中c的值
w_0 = m_t - w_1*m_x;
%% 在画板上绘制出数据集的点
figure(1);hold off
plot(x,y,'bo','markersize',5,'linewidth',2)
set(gca,'xtick',0:1:25)
% 画布大小为25*25
xplot = [0 25];
yplot = [0 25];
xlim(xplot)
ylim(yplot)
hold on
% 打印出拟合的线段
plot(xplot,w_0+w_1*xplot,'r','linewidth',2)
set(gca,'yTick',0:1:150)
xlabel('x');
ylabel('y');
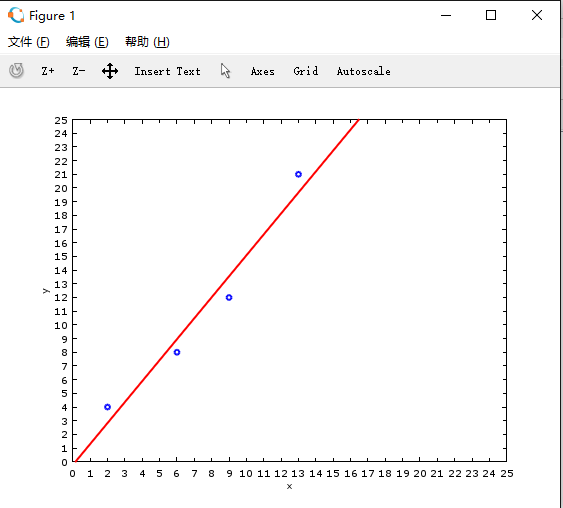
运行结果