【CVPR2022】On the Integration of Self-Attention and Convolution
【CVPR2022】On the Integration of Self-Attention and Convolution
卷积和自注意力是表征学习的两种强大技术，它们通常被认为是两种截然不同的对等方法。在这个论文中，作者表明它们之间存在很强的潜在关系，并将二者高效结合在一起。
这个论文首先首先证明了k×k的传统卷积可以分解为\(k^2\) 个单独的1×1卷积。然后，将self-attention模块中queries, keys, values的投影解释为多个1×1卷积，然后计算注意权重和values的聚合。因此，两个模块的第一阶段包括类似的操作。更重要的是，与第二阶段相比，第一阶段的计算复杂度占主导地位（通道大小的平方）。作者思路如下图所示：
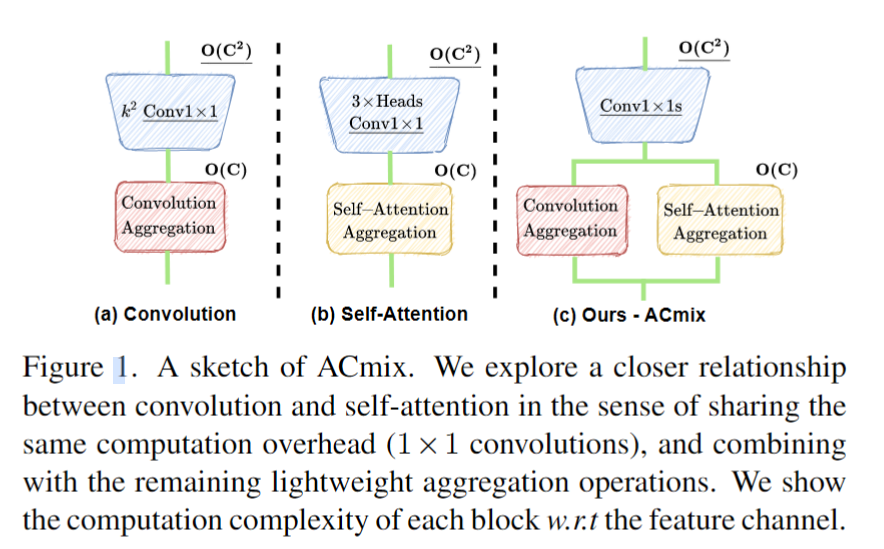
1、背景与动机
卷积算法是根据卷积核内内容的加权和，卷积核是全局共享的，为特征图添加了重要的归纳偏置。自注意力计算的是全局信息的加权平均，通过计算相关像素对之间的相似函数动态获得注意力权重，这种灵活性使自注意力模块可以自适应地关注不同区域，捕获更多的特征信息。
考虑到卷积和自注意力两者之间的不同以及互补性质，通过整合模块可能会从这两种范式中获益。当前大多方法的处理是：使用自注意力增强卷积模块；使用自注意力模块代替卷积模块；同时使用自注意力和卷积两种机制，但是分成了独立的路径，没有将二者真正结合。
总之，卷积和自注意力的内在联系没有得到充分挖掘。这篇论文试图挖掘自注意力和卷积之间更为密切的关系。
2、主要方法
（1）卷积
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hrhggRBn-1655485157601)(D:\pic\image-20220615215715815.png)]
传统卷积会通过k*k卷积核特征转换后，先聚合后再偏移进入下个位置再卷积，这里的卷积是通过1*1卷积核计算feature map所有的特征转换后，先偏移，再聚合，将其拆分成变换和偏移聚合两个阶段（如上图所示）：
- 第一步是卷积操作将kxk的卷积核拆分成kxk个1x1的卷积核，计算出每个kernel中的每个元素与feature map 相乘的值，不做加和处理，所以有k x k x cin x cout的计算量
- 第二步，是通过1x1的卷积核卷积后，需要对应到kxk的标准卷积上，那就需要将各个位置对应上在相加，第一个公式则是移位操作，第二个公式是对移位后的值在对应位置上加和操作，计算量为k x k x cout，第二步将第一步的输出进行加和，没有新的参数出来，所以参数量为0，计算量上，移位操作没有计算量的产生，总计算量为k x k x cout。
（2）Self-attention
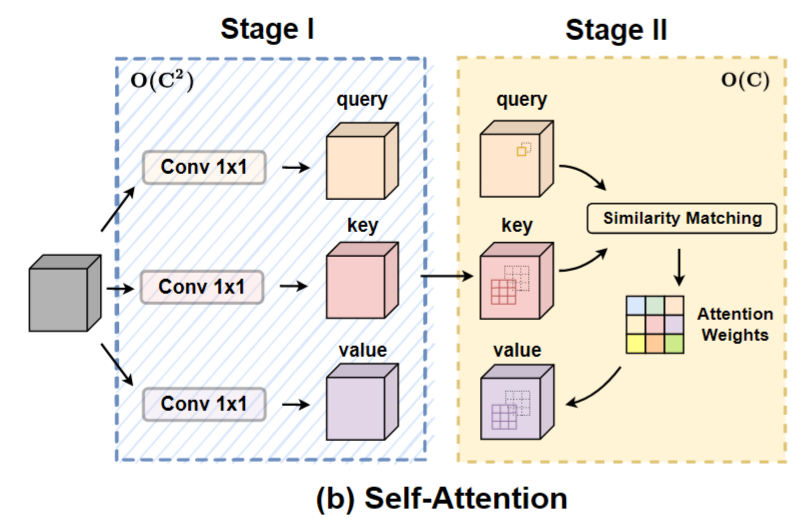
自注意力的计算也可以看作是两步：
- 第一步，通过1x1的卷积变换后，计算出quey，key，value。其实1X1的卷积可以等同于全连接。
- 第二步，对quey，key，value进行注意力权重的计算和 multi-head 拼接 操作，因为此时只考虑窗口kxk范围内的元素，即收集局部特征，所以计算量中序列长度也是固定的为kxk。所以在quey和key的计算中，计算量为kxcxk，在quey x key和value的计算中，计算量为kxkxc。所以整体为2倍kxkxc。而且此时没有额外的需要学习的参数，所以参数量为0。
这里进行QKV计算时，应该采用了一些独特的计算方法，论文里没有具体说明，但根据论文里的图示，我的理解是：query 里的一个像素，在key里取对应的3X3邻域进行相似度计算，得到一个3x3的权重矩阵，然后对 value 里的 3x3 区域进行加权计算得到 self-attention 的结果。（非常像 Neighborhood attention transformer，核心思路都是基本上一样的，不过 NAT 实现时有大量的CUDA代码，但 ACMix 里的attention 是完全用 pytorch 实现的）
q, k, v = self.conv1(x), self.conv2(x), self.conv3(x)
scaling = float(self.head_dim) ** -0.5
b, c, h, w = q.shape
# multi-head
q_att = q.view(b*self.head, self.head_dim, h, w) * scaling
k_att = k.view(b*self.head, self.head_dim, h, w)
v_att = v.view(b*self.head, self.head_dim, h, w)
# b*head, head_dim, k_att^2, h_out, w_out
unfold_k = self.unfold(self.pad_att(k_att)).view(b*self.head, self.head_dim, self.kernel_att*self.kernel_att, h_out, w_out)
# 位置编码：1, head_dim, k_att^2, h_out, w_out
unfold_rpe = self.unfold(self.pad_att(pe)).view(1, self.head_dim, self.kernel_att*self.kernel_att, h_out, w_out)
# 计算 Q 和 K 的相似性，两个张量逐元素相乘，最后在 head_dim 维度求和
# (b*head, head_dim, 1, h_out, w_out) * (b*head, head_dim, k_att^2, h_out, w_out) -> (b*head, k_att^2, h_out, w_out)
att = (q_att.unsqueeze(2)*(unfold_k + q_pe.unsqueeze(2) - unfold_rpe)).sum(1)
# softmax 归一化
att = self.softmax(att)
# V fold 成 (b*head, head_dim, k_atten^2, h_out, w_out )
out_att = self.unfold(self.pad_att(v_att)).view(b*self.head, self.head_dim, self.kernel_att*self.kernel_att, h_out, w_out)
# 权重矩阵和 fold 后的 V 相乘，然后在 k_att^2 这个维度求和
out_att = (att.unsqueeze(1) * out_att).sum(2).view(b, self.out_planes, h_out, w_out)
（3）总体框架
论文总体框架如下图所示，
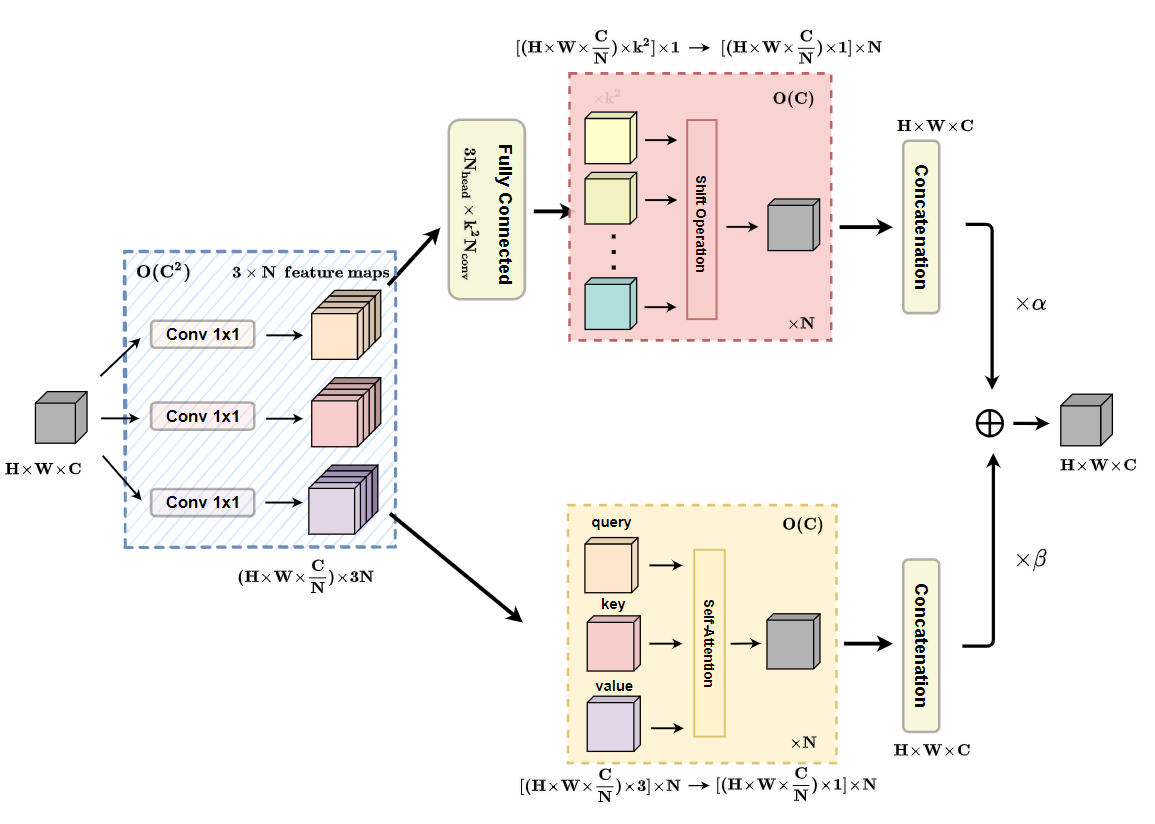
第一阶段： 通过3个1x1的卷积，生成3个feature map（主要是针对self attention的q、k和v），并将3个feature map分别在深度方向上分为N组(针对self attention的N 个 heads)。
第二阶段： 卷积部分，先通过通道层的全连接对通道扩张，后面处理和卷积第二步的处理相同，先对其偏移后，再去聚合成对应的维度。自注意力部分，按照上面的描述进行计算就可以。最后，将两个分支进行融合\(F_\text{out}=\alpha F_\text{att}+\beta F_\text{conv}\)，系数\(\alpha\)和\(\beta\)为可以学习的参数。
3、实验与分析
图像分类实验中，在参数占优的情况下，显著提升了准确率。
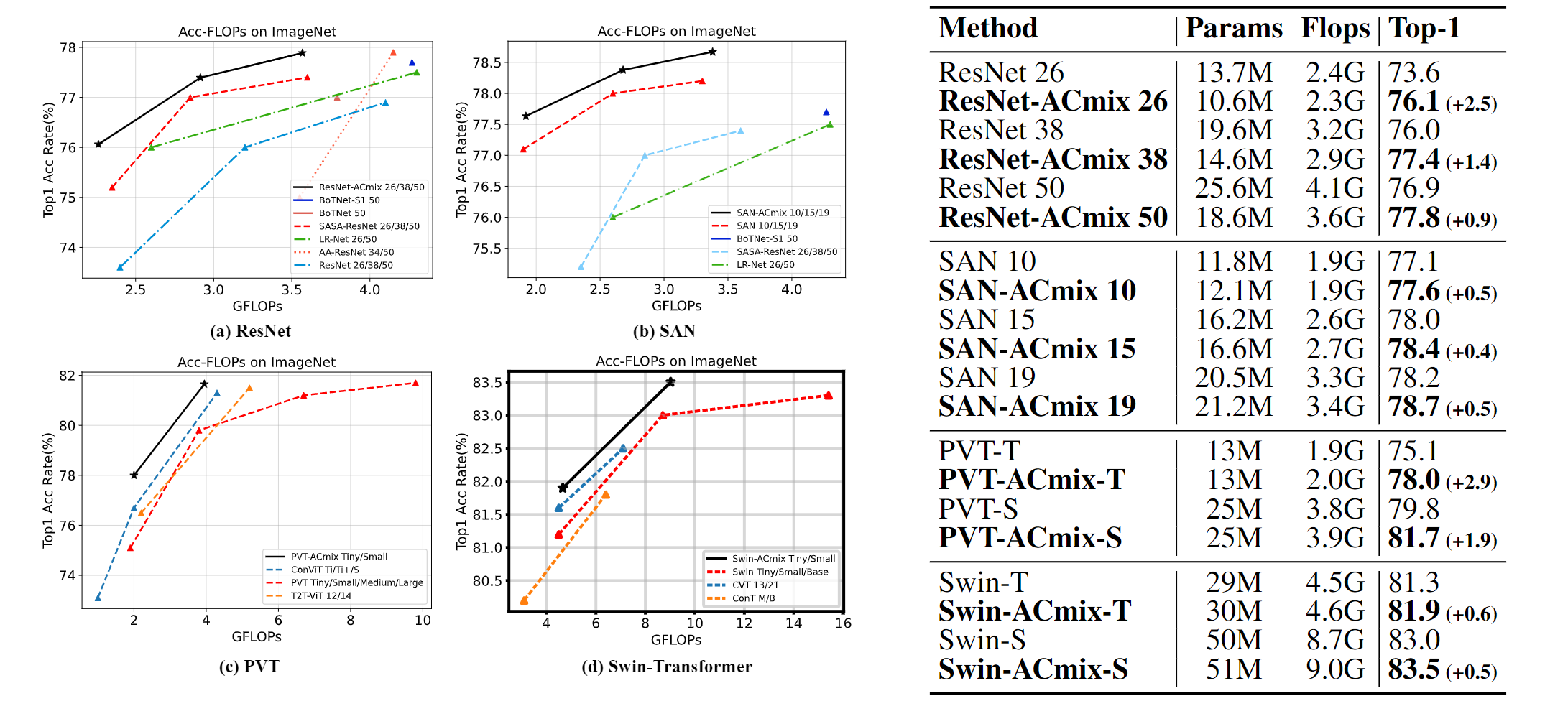
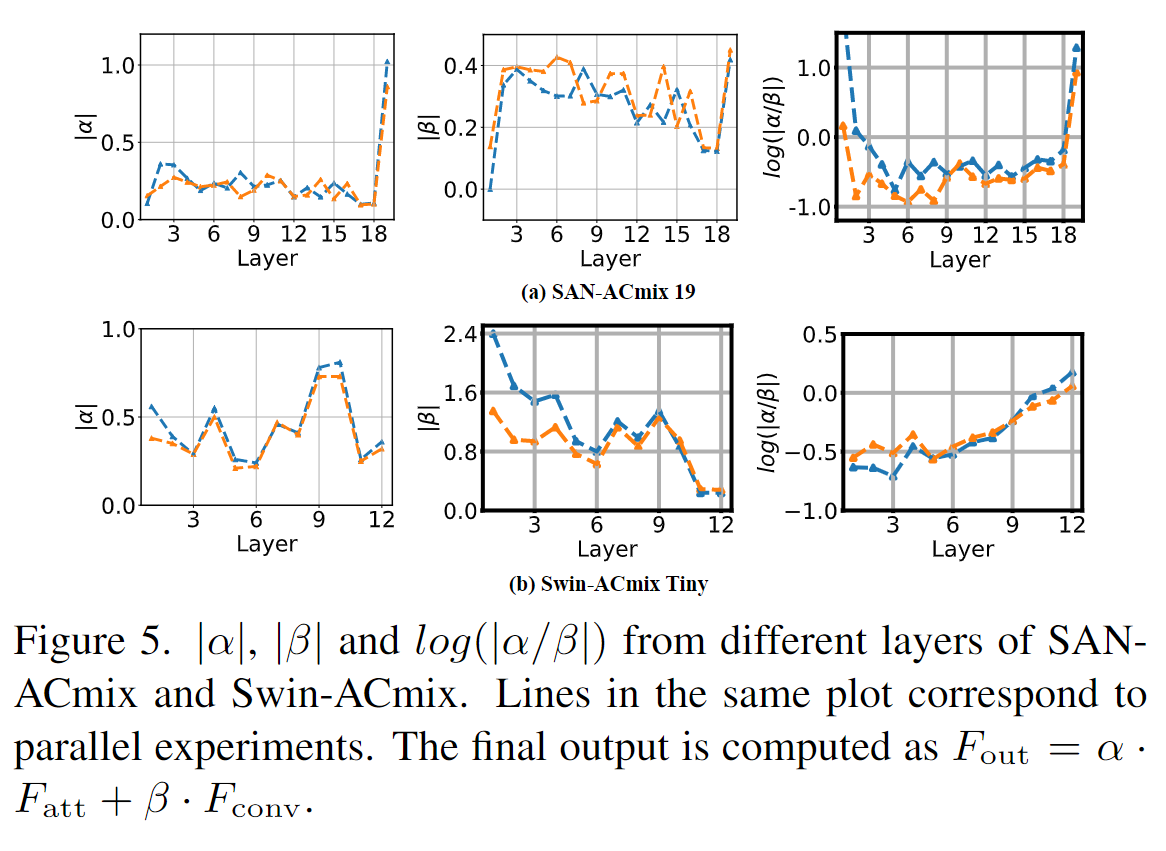
有趣的实验是，卷积 和 attention 两个部分权重的可视化，可以看出，网络浅期是卷积占主导地位，网络深层是 self-attention 占主导地位。（必须吐槽一下，图中两种颜色的线貌似没有说明，不清楚分别指的是什么。从第一行里，也看不出来作者描述的结论）
