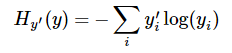1、求loss:tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits, labels, name=None))
1.求loss:
tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits, labels, name=None))
第一个参数logits:就是神经网络最后一层的输出,如果有batch的话,它的大小就是[batchsize,num_classes],单样本的话,大小就是num_classes
第二个参数labels:实际的标签,大小同上
具体的执行流程大概分为两步:
第一步是先对网络最后一层的输出做一个softmax,这一步通常是求取输出属于某一类的概率,对于单样本而言,输出就是一个num_classes([Y1,Y2,Y3...]其中Y1,Y2,Y3...分别代表了是属于该类的概率第二步是softmax的输出向量[Y1,Y2,Y3...]和样本的实际标签做一个交叉熵,公式如下:
其中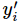
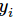
softmax的输出向量[Y1,Y2,Y3...]
显而易见,预测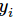
注意!!!这个函数的返回值并不是一个数,而是一个向量,如果要求交叉熵,我们要再做一步tf.reduce_sum操作,就是对向量里面所有元素求和,最后才得到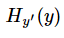
tf.reduce_mean操作,对向量求均值!
import tensorflow as tf logits=tf.constant([[1.0,2.0,3.0],[1.0,2.0,3.0],[1.0,2.0,3.0]]) y=tf.nn.softmax(logits) y_=tf.constant([[0.0,0.0,1.0],[0.0,0.0,1.0],[0.0,0.0,1.0]]) cross_entropy = -tf.reduce_sum(y_*tf.log(y)) #交叉熵公式 cross_entropy2=tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=y_))#代入函数 with tf.Session() as sess: softmax=sess.run(y) c_e = sess.run(cross_entropy) c_e2 = sess.run(cross_entropy2) print("step1:softmax result=") print(softmax) print("step2:cross_entropy result=") print(c_e) print("Function(softmax_cross_entropy_with_logits) result=") print(c_e2)
step1:softmax result=
[[0.09003057 0.24472848 0.66524094]
[0.09003057 0.24472848 0.66524094]
[0.09003057 0.24472848 0.66524094]]
step2:cross_entropy result=
1.222818
Function(softmax_cross_entropy_with_logits) result=
1.2228179