差分约束

差分约束系统

在一个差分约束系统(system of difference constraints)中，线性规划矩阵A的每一行包含一个1和一个-1，A的其他所有元素都为0。因此，由Ax≤b给出的约束条件是m个差分约束集合，其中包含n个未知量，对应的线性规划矩阵A为m行n列。每个约束条件为如下形式的简单线性不等式：xj-xi≤bk。其中1≤i,j≤n，1≤k≤m。

例如，考虑这样一个问题，寻找一个5维向量x=(xi)以满足：

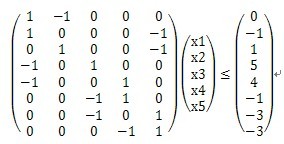
这一问题等价于找出未知量xi，i=1,2,…,5，满足下列8个差分约束条件：

x1-x2≤0

x1-x5≤-1

x2-x5≤1

x3-x1≤5

x4-x1≤4

x4-x3≤-1

x5-x3≤-3

x5-x4≤-3

该问题的一个解为x=(-5,-3,0,-1,-4)，另一个解y=(0,2,5,4,1)，这2个解是有联系的：y中的每个元素比x中相应的元素大5。

引理：设x=(x1,x2,…,xn)是差分约束系统Ax≤b的一个解，d为任意常数。则x+d=(x1+d,x2+d,…,xn+d)也是该系统Ax≤b的一个解。

http://poj.org/problem?id=3159

给n个人派糖果，给出m组数据，每组数据包含A，B，c  三个数，
意思是A的糖果数比B少的个数不多于c,即B的糖果数 - A的糖果数<= c 。
最后求n 比 1 最多多多少糖果。

算是裸题 v-u《=w 建有向边 u-》v 权值w 若有负环无解

 //大-小<=c ,有向边(小，大）：c

如果是大于等于的转化一下如下

//大-小>=c,小-大<=-c,有向边(大，小):-c

【解题思路】
这是一题典型的差分约束题。不妨将糖果数当作距离，把相差的最大糖果数看成有向边AB的权值，
我们得到 dis[B]-dis[A]<=w(A,B)。看到这里，我们联想到求最短路时的松弛技术，
即if(dis[B]>dis[A]+w(A,B), dis[B]=dis[A]+w(A,B)。
即是满足题中的条件dis[B]-dis[A]<=w(A,B），由于要使dis[B] 最大，
所以这题可以转化为最短路来求。
这题如果用SPFA 算法的话，则需要注意不能用spfa+queue 来求,会TLE ，而是用 spfa + stack

我用了priority的dij 因为题目保证了有解

 1 #include<cstdio>
 2 #include<queue>
 3 using namespace std;
 4 const int inf=0x3f3f3f3f;
 5 class Dijkstra { ///单源最短路 o(ME*log(MV))
 6     typedef int typec;///边权的类型
 7     static const int ME=2e5+10;///边的个数
 8     static const int MV=3e4+10;///点的个数
 9     struct Q {
10         int id;
11         typec w;
12         friend bool operator <(const Q &a,const Q &b) {
13             return a.w>b.w;
14         }
15     } now;
16     priority_queue<Q> q;
17     struct E {
18         int v,next;
19         typec w;
20     } e[ME];
21     int n,le,head[MV],u,v,i;
22     typec dist[MV],w;
23     bool used[MV];
24 public:
25     void init(int tn) {///传入点的个数
26         n=tn;
27         le=0;
28         for(i=0; i<=n; i++) head[i]=-1;
29     }
30     void add(int u,int v,typec w) {
31         e[le].v=v;
32         e[le].w=w;
33         e[le].next=head[u];
34         head[u]=le++;
35     }
36     void solve(int s) {///传入起点
37         for(i=0; i<=n; i++) {
38             used[i]=true;
39             dist[i]=inf;
40         }
41         dist[s]=0;
42         now.id=s;
43         now.w=0;
44         while(!q.empty()) q.pop();
45         q.push(now);
46         while(!q.empty()) {
47             now=q.top();
48             q.pop();
49             u=now.id;
50             if(used[u]) {
51                 used[u]=false;
52                 for(i=head[u]; ~i; i=e[i].next) {
53                     v=e[i].v;
54                     w=e[i].w;
55                     if(used[v]&&dist[v]>w+dist[u]) {
56                         dist[v]=w+dist[u];
57                         now.id=v;
58                         now.w=dist[v];
59                         q.push(now);
60                     }
61                 }
62             }
63         }
64     }
65     typec getdist(int id) {
66         return dist[id];
67     }
68 } g;
69 
70 int main(){
71     int n,m,u,v,w;
72     while(~scanf("%d%d",&n,&m)){
73         g.init(n);
74         while(m--){
75             scanf("%d%d%d",&u,&v,&w);
76             g.add(u,v,w);
77         }
78         g.solve(1);
79         printf("%d\n",g.getdist(n));
80     }
81     return 0;
82 }

View Code

poj http://poj.org/problem?id=3169

有》=也有《=，大于等于的移项一下，还是跟小于等于一样的建边，有负环是无解，最短路是inf是任意解，有最短路就是唯一解

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 #include<queue>
 5 #include<stack>
 6 #define mt(a,b) memset(a,b,sizeof(a))
 7 using namespace std;
 8 const int inf=0x3f3f3f3f;
 9 class Spfa { ///单源最短路o(k*ME)k~=2
10     typedef int typec;///边权的类型
11     static const int ME=2e4+10;///边的个数
12     static const int MV=1e3+10;///点的个数
13     struct E {
14         int v,next;
15         typec w;
16     } e[ME];
17     int n,le,head[MV],inque[MV],i,u,v;
18     typec dist[MV];
19     bool used[MV];
20     queue<int> q;
21 public:
22     void init(int tn) { ///传入点的个数
23         n=tn;
24         le=0;
25         for(i=0; i<=n; i++) head[i]=-1;
26     }
27     void add(int u,int v,typec w) {
28         e[le].v=v;
29         e[le].w=w;
30         e[le].next=head[u];
31         head[u]=le++;
32     }
33     bool solve(int s) { ///传入起点,存在负环返回false
34         for(i=0; i<=n; i++) {
35             dist[i]=inf;
36             used[i]=true;
37             inque[i]=0;
38         }
39         used[s]=false;
40         dist[s]=0;
41         inque[s]++;
42         while(!q.empty()) q.pop();
43         q.push(s);
44         while(!q.empty()) {
45             u=q.front();
46             q.pop();
47             used[u]=true;
48             for(i=head[u]; ~i; i=e[i].next) {
49                 v=e[i].v;
50                 if(dist[v]>dist[u]+e[i].w) {
51                     dist[v]=dist[u]+e[i].w;
52                     if(used[v]) {
53                         used[v]=false;
54                         q.push(v);
55                         inque[v]++;
56                         if(inque[v]>n) return false;
57                     }
58                 }
59             }
60         }
61         return true;
62     }
63     typec getdist(int id) {
64         return dist[id];
65     }
66 } g;
67 int main() {
68     int n;
69     int ML,MD;
70     int a,b,c;
71     while(~scanf("%d%d%d",&n,&ML,&MD)) {
72         g.init(n);
73         while(ML--) {
74             scanf("%d%d%d",&a,&b,&c);
75             if(a>b)swap(a,b);//注意加边顺序
76             g.add(a,b,c);
77             //大-小<=c ,有向边(小，大）：c
78         }
79         while(MD--) {
80             scanf("%d%d%d",&a,&b,&c);
81             if(a<b)swap(a,b);
82             g.add(a,b,-c);
83             //大-小>=c,小-大<=-c,有向边(大，小):-c
84         }
85         if(!g.solve(1)) printf("-1\n");//无解
86         else if(g.getdist(n)==inf) printf("-2\n");
87         else printf("%d\n",g.getdist(n));
88     }
89     return 0;
90 }

View Code

posted on 2015-05-06 22:42 gaolzzxin 阅读(208) 评论(0) 编辑收藏举报