luogu3629
P3629 [APIO2010]巡逻
题目描述
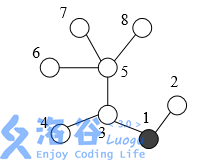
在一个地区中有 n 个村庄,编号为 1, 2, ..., n。有 n – 1 条道路连接着这些村 庄,每条道路刚好连接两个村庄,从任何一个村庄,都可以通过这些道路到达其 他任一个村庄。每条道路的长度均为 1 个单位。 为保证该地区的安全,巡警车每天要到所有的道路上巡逻。警察局设在编号 为 1 的村庄里,每天巡警车总是从警察局出发,最终又回到警察局。 下图表示一个有 8 个村庄的地区,其中村庄用圆表示(其中村庄 1 用黑色的 圆表示),道路是连接这些圆的线段。为了遍历所有的道路,巡警车需要走的距 离为 14 个单位,每条道路都需要经过两次。
为了减少总的巡逻距离,该地区准备在这些村庄之间建立 K 条新的道路, 每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束 (见下面的图例(c))。 一条新道路甚至可以是一个环,即,其两端连接到同一 个村庄。 由于资金有限,K 只能是 1 或 2。同时,为了不浪费资金,每天巡警车必须 经过新建的道路正好一次。 下图给出了一些建立新道路的例子:
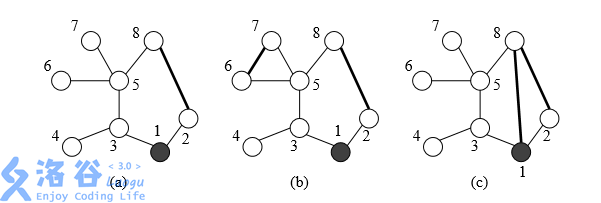
在(a)中,新建了一条道路,总的距离是 11。在(b)中,新建了两条道路,总 的巡逻距离是 10。在(c)中,新建了两条道路,但由于巡警车要经过每条新道路 正好一次,总的距离变为了 15。 试编写一个程序,读取村庄间道路的信息和需要新建的道路数,计算出最佳 的新建道路的方案使得总的巡逻距离最小,并输出这个最小的巡逻距离。
输入格式
第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1 行,每行两个整数 a, b, 表示村庄 a 与 b 之间有一条道路(1 ≤ a, b ≤ n)。
输出格式
输出一个整数,表示新建了 K 条道路后能达到的最小巡逻距离。
输入输出样例
8 1
1 2
3 1
3 4
5 3
7 5
8 5
5 6
11
8 2
1 2
3 1
3 4
5 3
7 5
8 5
5 6
10
5 2
1 2
2 3
3 4
4 5
6
说明/提示
10%的数据中,n ≤ 1000, K = 1;
30%的数据中,K = 1;
80%的数据中,每个村庄相邻的村庄数不超过 25;
90%的数据中,每个村庄相邻的村庄数不超过 150; 100%的数据中,3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。
sol:一开始有一个很fp的idea(大雾,就是找到一条直径以后再找一条不重复的次长链,就被ztn用下面这样的树叉掉了%%%ztnakking
显然找到最长链以后应该把中间两条连起来最优,这样就是把之前的直径上的边边权改为-1,因为如果再走会对答案造成负贡献,之前其实已经减掉了,在减-1相当于+1,然后在用dp跑一遍直径就好了

#include <bits/stdc++.h> using namespace std; typedef int ll; inline ll read() { ll s=0; bool f=0; char ch=' '; while(!isdigit(ch)) {f|=(ch=='-'); ch=getchar();} while(isdigit(ch)) {s=(s<<3)+(s<<1)+(ch^48); ch=getchar();} return (f)?(-s):(s); } #define R(x) x=read() inline void write(ll x) { if(x<0) {putchar('-'); x=-x;} if(x<10) {putchar(x+'0'); return;} write(x/10); putchar((x%10)+'0'); } #define W(x) write(x),putchar(' ') #define Wl(x) write(x),putchar('\n') const int N=200005,M=400005,inf=0x3f3f3f3f; int n,k; #define pii pair<int,int> #define Mp make_pair #define fi first #define se second pii rt1,rt2; int tot=0,Next[M],to[M],val[M],head[N],dep[N],fae[N],fa[N],dp[N][2]; bool inq[N],Bo[N]; inline void Link(int x,int y,int z) { Next[++tot]=head[x]; to[tot]=y; val[tot]=z; head[x]=tot; } inline pii bfs(int s) { int i,dd=0; queue<int>Que; memset(inq,0,sizeof inq); fa[s]=0; fae[s]=dep[s]=0; Que.push(s); inq[s]=1; while(!Que.empty()) { int x=Que.front(); Que.pop(); if(dep[x]>dep[dd]) dd=x; for(i=head[x];i;i=Next[i]) if(!inq[to[i]]) { fa[to[i]]=x; fae[to[i]]=i; dep[to[i]]=dep[x]+1; inq[to[i]]=1; Que.push(to[i]); } } return Mp(dd,dep[dd]); } inline void dfs(int x,int fat) { int e; dp[x][0]=dp[x][1]=0; for(e=head[x];e;e=Next[e]) if(to[e]!=fat) { // cout<<x<<' '<<to[e]<<' '<<val[e]<<endl; dfs(to[e],x); int tmp=dp[to[e]][0]+val[e]; // if(x==5) cout<<to[e]<<' '<<"tmp="<<tmp<<endl; dp[x][1]=max(dp[x][1],tmp+dp[x][0]); dp[x][0]=max(dp[x][0],tmp); } } int main() { int i,x,y,ans=-inf; R(n); R(k); for(i=1;i<n;i++) { R(x); R(y); Link(x,y,1); Link(y,x,1); } rt1=bfs(1); rt2=bfs(rt1.fi); if(k==1) Wl((n-1)*2-(rt2.se-1)); else { int oo=rt2.fi; while(oo!=rt1.fi) { // cout<<"oo="<<oo<<' '<<fa[oo]<<" "<<fae[oo]<<endl; val[fae[oo]]=val[(fae[oo]&1)?(fae[oo]+1):(fae[oo]-1)]=-1; oo=fa[oo]; } dfs(rt1.fi,0); for(i=1;i<=n;i++) { // cout<<"i:"<<i<<' '<<dp[i][0]<<' '<<dp[i][1]<<endl; ans=max(ans,dp[i][1]); } Wl((n-1)*2-(rt2.se-1)-(ans-1)); } return 0; } /* input 8 1 1 2 3 1 3 4 5 3 7 5 8 5 5 6 output 11 input 8 2 1 2 3 1 3 4 5 3 7 5 8 5 5 6 output 10 */




