洛谷P2698 [USACO12MAR]花盆Flowerpot

P2698 [USACO12MAR]花盆Flowerpot

题目描述

Farmer John has been having trouble making his plants grow, and needs your help to water them properly. You are given the locations of N raindrops (1 <= N <= 100,000) in the 2D plane, where y represents vertical height of the drop, and x represents its location over a 1D number line:

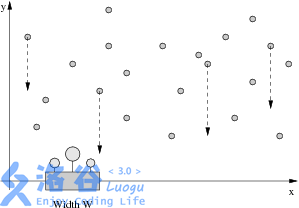
Each drop falls downward (towards the x axis) at a rate of 1 unit per second. You would like to place Farmer John's flowerpot of width W somewhere along the x axis so that the difference in time between the first raindrop to hit the flowerpot and the last raindrop to hit the flowerpot is at least some amount D (so that the flowers in the pot receive plenty of water). A drop of water that lands just on the edge of the flowerpot counts as hitting the flowerpot.

Given the value of D and the locations of the N raindrops, please compute the minimum possible value of W.

老板需要你帮忙浇花。给出N滴水的坐标，y表示水滴的高度，x表示它下落到x轴的位置。

每滴水以每秒1个单位长度的速度下落。你需要把花盆放在x轴上的某个位置，使得从被花盆接着的第1滴水开始，到被花盆接着的最后1滴水结束，之间的时间差至少为D。

我们认为，只要水滴落到x轴上，与花盆的边沿对齐，就认为被接住。给出N滴水的坐标和D的大小，请算出最小的花盆的宽度W。

输入输出格式

输入格式：

第一行2个整数 N 和 D。

第2.. N+1行每行2个整数，表示水滴的坐标(x,y)。

输出格式：

仅一行1个整数，表示最小的花盆的宽度。如果无法构造出足够宽的花盆，使得在D单位的时间接住满足要求的水滴，则输出-1。

输入输出样例

输入样例#1： 

4 5
6 3
2 4
4 10
12 15

输出样例#1： 

2

说明

【样例解释】

有4滴水， (6,3), (2,4), (4,10), (12,15).水滴必须用至少5秒时间落入花盆。花盆的宽度为2是必须且足够的。把花盆放在x=4..6的位置，它可以接到1和3水滴, 之间的时间差为10-3 = 7满足条件。

【数据范围】

40%的数据：1 ≤ N ≤ 1000，1 ≤ D ≤ 2000；

100%的数据：1 ≤ N ≤ 100000，1 ≤ D ≤ 1000000，0≤x,y≤10^6。

 

sol：单调队列蛮显然的吧（其实接近板子题）

维护一个递增的单调队列，当队尾与队首的高度差>D时弹队首，当队尾比当前元素大时弹队尾

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read()
{
    ll s=0;
    bool f=0;
    char ch=' ';
    while(!isdigit(ch))
    {
        f|=(ch=='-'); ch=getchar();
    }
    while(isdigit(ch))
    {
        s=(s<<3)+(s<<1)+(ch^48); ch=getchar();
    }
    return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
    if(x<0)
    {
        putchar('-'); x=-x;
    }
    if(x<10)
    {
        putchar(x+'0');    return;
    }
    write(x/10);
    putchar((x%10)+'0');
    return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const int N=100005,inf=0x3f3f3f3f;
int n,D;
struct Shuidi
{
    ll X,Y;
}Water[N];
inline bool cmp(Shuidi p,Shuidi q)
{
    return p.X<q.X;
}
struct Record
{
    ll Weiz,Shuz;
}Ddq[N];
int main()
{
    int i,j;
    R(n); R(D);
    for(i=1;i<=n;i++)
    {
        int x=read(),y=read();
        Water[i]=(Shuidi){x,y};
    }
    sort(Water+1,Water+n+1,cmp);
    int Head=1,Tail=0;
    ll ans=inf;
    for(i=1;i<=n;i++)
    {
        while(Head<Tail&&Water[Ddq[Head+1].Weiz].Y+D<=Water[Ddq[Tail].Weiz].Y) Head++;
        if(Water[Ddq[Head].Weiz].Y+D<=Water[Ddq[Tail].Weiz].Y) ans=min(ans,Ddq[Tail].Shuz-Ddq[Head].Shuz);
        while(Head<=Tail&&Water[Ddq[Tail].Weiz].Y>Water[i].Y) Tail--;
        Ddq[++Tail]=(Record){i,Water[i].X};
    }
    if(ans==inf) puts("-1");
    else Wl(ans);
    return 0;
}
/*
input
4 5
6 3
2 4
4 10
12 15
output
2
*/