一本通1660「一本通 6.6 练习 9」网格

题目描述

原题来自：BZOJ 3907

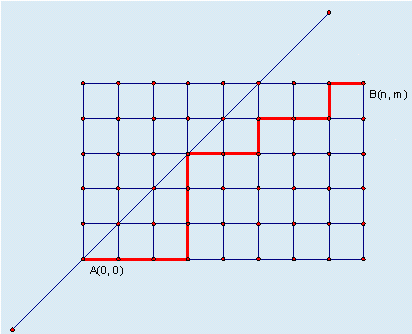
某城市的街道呈网格状，左下角坐标为 A(0, 0)，右上角坐标为 B(n, m)，其中 n≥m。现在从 A(0, 0) 点出发，只能沿着街道向正右方或者正上方行走，且不能经过图示中直线左上方的点，即任何途径的点 (x,y) 都要满足 x≥y，请问在这些前提下，到达 B(n, m) 有多少种走法。

输入格式

仅有一行，包含两个整数 n 和 m，表示城市街区的规模。

输出格式

仅有一个整数和一个换行回车符，表示不同的方案总数。

样例

样例输入

6 6

样例输出

132

数据范围与提示

对于全部数据，1≤m≤n≤5000。

 

sol：那幅图看上去就很像卡特兰数的那张图，不过卡特兰数满足n=m

其实差不多，答案就是C(n+m,n)-C(n+m,n+1)

Ps:python偷懒

Jiec={};
def C(n,m):
    return Jiec[n]/Jiec[m]/Jiec[n-m];
Jiec[0]=1;
for i in range(1,10000):
    Jiec[i]=Jiec[i-1]*i;
f=raw_input().split(" ");
n=int(f[0]); m=int(f[1]);
print(C(n+m,n)-C(n+m,n+1));