一本通1581旅游规划
1581:旅游规划
时间限制: 1000 ms 内存限制: 524288 KB
描述
W市的交通规划出现了重大问题,市政府下决心在全市的各大交通路口安排交通疏导员来疏导密集的车流。但由于人员不足,W市市长决定只在最需要安排人员的路口安放人员。具体说来,W市的交通网络十分简单,它包括n个交叉路口和n-1条街道,任意一条街道连接两个交叉路口,并且任意两个交叉路口之间都存在一条路径互相连接。经过长期调查结果显示如果一个交叉路口位于W市交通网的最长路径上,那么这个路口必然拥挤不堪,所谓最长路径定义为某条路径p=(v1,v2,v3…vk),路径经过的路口各不相同且城市中不存在长度>k的路径(因此可能存在着不唯一的最长路径)。因此W市市长希望知道有哪些路口位于城市交通网的最长路径之上。
格式
输入格式
第一行包括一个整数n。
之后的n-1行每行包括两个整数u, v表示编号为u和v的路口之间存在着一条街道(注意:路口被依次编号为0到n-1)
输出格式
输出包括若干行,每行包括一个整数——某个位于最长路上路口的编号。
为了确保解唯一,我们规定位于所有最长路上的路口按编号顺序从小到大输出。
样例1
样例输入1
10
0 1
0 2
0 4
0 6
0 7
1 3
2 5
4 8
6 9
样例输出1
0
1
2
3
4
5
6
8
9
提示
这里存在着若干条最长路径,其中的两条是3-1-0-2-5与8-4-0-6-9,他们的长度都是5,但是不存在长度>5的路径且所有最长路径都不包括路口7,所以答案中没有7。
数据范围:
对于50%的数据保证n<=1000
对于100%的数据保证n<=200000
先附上手绘的样例图(过于丑陋)
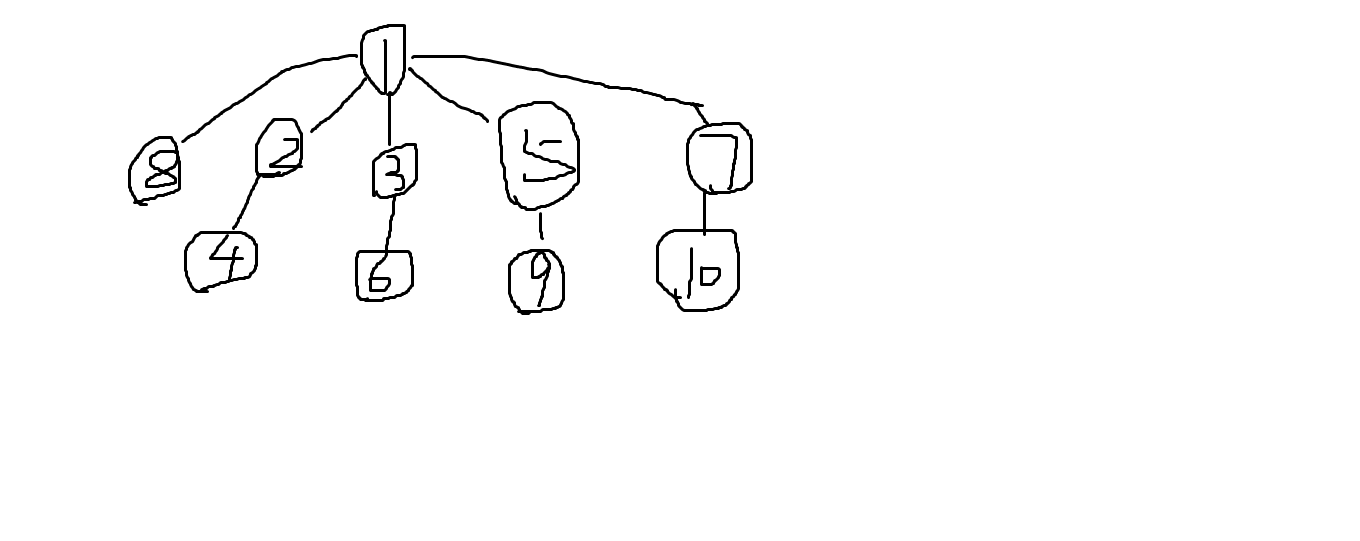
sol:一开始想求出直径的两个端点然后差分搞一下,然后发现非常wei,然后就想到如果一点在直径上,那么他不是只有两个方向延伸吗?(向儿子,或者向上爬几步爬到根或者爬到别的子树里去);所以两遍dfs就可以求出两个方向的最长值,还有注意下因为Up[x]=max(Up[fa]+1,Down[fa]+1),但是如果Down[fa]最大值就是x转移过来的话,要用Down[fa]的次大值来转移,所以Down要记录Zd和Cd

#include <bits/stdc++.h> using namespace std; inline int read() { int s=0; bool f=0; char ch=' '; while(!isdigit(ch)) { f|=(ch=='-'); ch=getchar(); } while(isdigit(ch)) { s=(s<<3)+(s<<1)+(ch^48); ch=getchar(); } return (f)?(-s):(s); } #define R(x) x=read() inline void write(int x) { if(x<0) { putchar('-'); x=-x; } if(x<10) { putchar(x+'0'); return; } write(x/10); putchar((x%10)+'0'); return; } inline void writeln(int x) { write(x); putchar('\n'); return; } #define W(x) write(x),putchar(' ') #define Wl(x) writeln(x) const int N=200005,M=400005; int n; struct Tree { int tot,Next[M],to[M],head[N]; inline void add(int x,int y) { Next[++tot]=head[x]; to[tot]=y; head[x]=tot; return; } int Down_Zd[N],From_Zd[N],Down_Cd[N],From_Cd[N]; inline void dfs_Down(int x,int fa) { int i; for(i=head[x];i;i=Next[i]) if(to[i]!=fa) { dfs_Down(to[i],x); if(Down_Zd[to[i]]+1>Down_Zd[x]) { From_Cd[x]=From_Zd[x]; Down_Cd[x]=Down_Zd[x]; From_Zd[x]=to[i]; Down_Zd[x]=Down_Zd[to[i]]+1; } else if(Down_Zd[to[i]]+1>Down_Cd[x]) { From_Cd[x]=to[i]; Down_Cd[x]=Down_Zd[to[i]]+1; } } return; } int Up[N]; inline void dfs_Up(int x,int fa) { if(fa) { if(From_Zd[fa]!=x) Up[x]=max(Up[fa]+1,Down_Zd[fa]+1); else Up[x]=max(Up[fa]+1,Down_Cd[fa]+1); } int i; for(i=head[x];i;i=Next[i]) if(to[i]!=fa) { dfs_Up(to[i],x); } return; } inline void Output() { int i,ans=0; for(i=1;i<=n;i++) ans=max(ans,(Down_Zd[i]+Up[i],Down_Zd[i]+Down_Cd[i])); for(i=1;i<=n;i++) { // printf("@ %d %d\n",Down_Zd[i],Up[i]); if((Down_Zd[i]+Up[i]==ans)||(Down_Zd[i]+Down_Cd[i]==ans)) Wl(i-1); } return; } inline void Init() { tot=0; memset(head,0,sizeof head); return; } }T; int main() { int i; T.Init(); R(n); for(i=1;i<n;i++) { int x,y; x=read()+1; y=read()+1; T.add(x,y); T.add(y,x); } T.dfs_Down(1,0); T.dfs_Up(1,0); T.Output(); return 0; } /* input 10 0 1 0 2 0 4 0 6 0 7 1 3 2 5 4 8 6 9 output 0 1 2 3 4 5 6 7 8 9 */




