一本通1548【例 2】A Simple Problem with Integers

1548：【例 2】A Simple Problem with Integers

题目描述

这是一道模板题。

给定数列 a[1],a[2],…,a[n]，你需要依次进行 q 个操作，操作有两类：

• 1 l r x：给定 l,r,x，对于所有 i∈[l,r]，将 a[i] 加上 x（换言之，将 a[l],a[l+1],…,a[r] 分别加上 x）；
• 2 l r：给定 l,r，求 a[i]∑i=[l,r].​a[i] 的值（换言之，求 a[l]+a[l+1]+⋯+a[r] 的值）。

输入格式

第一行包含 2 个正整数 n,q，表示数列长度和询问个数。保证 1≤n,q≤10^6。
第二行 n 个整数 a[1],a[2],…,a[n]，表示初始数列。保证 ∣a[i]∣≤10^6。
接下来 q 行，每行一个操作，为以下两种之一：

• 1 l r x：对于所有 i∈[l,r]，将 a[i] 加上 x；
• 2 l r：输出 a[i]∑i=[l,r]​a[i] 的值。

保证 1≤l≤r≤n, ∣x∣≤10^6。

输出格式

对于每个 2 l r 操作，输出一行，每行有一个整数，表示所求的结果。

样例

样例输入

5 10
2 6 6 1 1
2 1 4
1 2 5 10
2 1 3
2 2 3
1 2 2 8
1 2 3 7
1 4 4 10
2 1 2
1 4 5 6
2 3 4

样例输出

15
34
32
33
50

数据范围与提示

对于所有数据，1≤n,q≤10^6, ∣a[i]∣≤10^6, 1≤l≤r≤n, ∣x∣≤10^6。

 

sol：树状数组模板题 想想怎么支持区间修改，

1）【区间修改单点查询】例如[L,R]这段区间+Tag，就是a[L]+Tag,a[R+1]-Tag

2）【区间修改区间查询】基于差分的思想 先想象一个d数组维护差分值 d[i]=a[i]-a[i-1]，基于差分的思想

a[i]=d[1]+d[2]+···+d[i-1]+d[i]，所以a[1~p]就是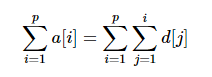，其中d[1]用了p次，d[2]用了p-1次，

转化一下可得，所以我们可以维护两个前缀和，

S1[i]=d[i],S2[i]=d[i]*i

 

查询：位置Pos的前缀和就是（Pos+1）*S1中1到Pos的和 减去 S2中1到Pos的和，[L,R]=SS[R]-SS[L-1]

修改：[L,R]   S1：S1[L]+Tag,S1[R+1]-Tag   S2：S2[L]+Tag*L ,S2[R+1]-Tag*(R+1）

 

#include <bits/stdc++.h>
using namespace std;
inline int read()
{
    int s=0,f=0;
    char ch=' ';
    while(!isdigit(ch))
    {
        f|=(ch=='-');
        ch=getchar();
    }
    while(isdigit(ch))
    {
        s=(s<<3)+(s<<1)+(ch^48);
        ch=getchar();
    }
    return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(long long x)
{
    if(x<0)
    {
        putchar('-');
        x=-x;
    }
    if(x<10)
    {
        putchar(x+'0');
        return;
    }
    write(x/10);
    putchar((x%10)+'0');
    return;
}
inline void writeln(long long x)
{
    write(x);
    putchar('\n');
    return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) writeln(x)
const int N=1000005;
int n,m,a[N];
struct BIT
{
    long long S1[N],S2[N];
    #define lowbit(x) ((x)&(-x))
    inline void Ins(int Pos,int Tag)
    {
        int PP=Pos;
        while(PP<=n)
        {
            S1[PP]+=Tag;
            S2[PP]+=1LL*Pos*Tag;
            PP+=lowbit(PP);
        }
        return;
    }
    inline long long Que(int Pos)
    {
        long long Sum=0;
        int PP=Pos;
        while(PP>0)
        {
            Sum+=1LL*(1LL*(Pos+1)*S1[PP]-S2[PP]);
            PP-=lowbit(PP);
        }
        return Sum;
    }
}T;
int main()
{
    int i;
    R(n); R(m);
    for(i=1;i<=n;i++)
    {
        R(a[i]);
        T.Ins(i,a[i]-a[i-1]);
    }
    for(i=1;i<=m;i++)
    {
        int opt,a,b,Tag;
        R(opt); R(a); R(b);
        switch (opt)
        {
            case 1:
                R(Tag);
                T.Ins(a,Tag);
                T.Ins(b+1,-Tag);
                break;
            case 2:
                Wl(1LL*T.Que(b)-1LL*T.Que(a-1));
                break;
        }
    }
    return 0;
}
/*
input
5 10
2 6 6 1 1
2 1 4
1 2 5 10
2 1 3
2 2 3
1 2 2 8
1 2 3 7
1 4 4 10
2 1 2
1 4 5 6
2 3 4
output
15
34
32
33
50
*/