MySQL Index--平衡树结构

树结构

==================================================
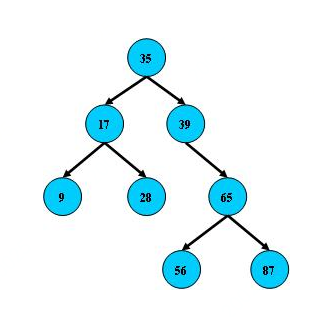
B树，即平衡二叉树,每个非叶子节点最多拥有两个子节点。
所有键值出现在叶子节点和非叶子节点。

==================================================

B-树，在B树上扩展出来的多路搜索树，每个非叶子节点可能包含N个子节点。
所有键值出现在叶子节点和非叶子节点。

==================================================

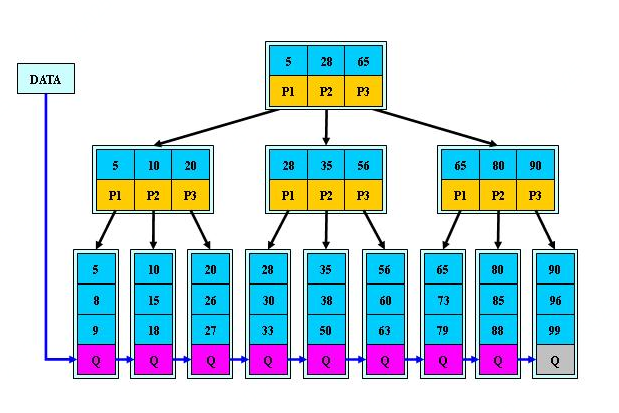
B+数，是B-数的变种，在所有叶子节点间增加链指针，且所有键值都出现在叶子节点。

==================================================

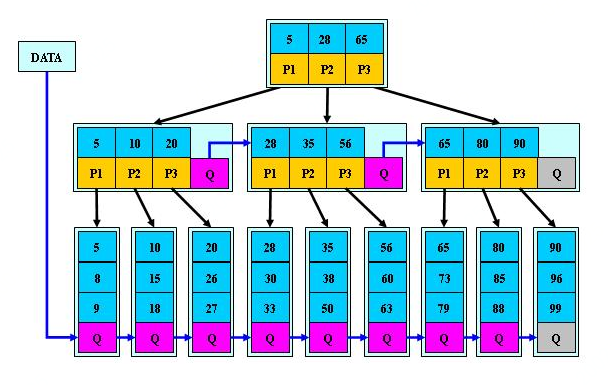
B*数：
B*树时在B+树的变体，在中间叶子节点之间增加指向兄弟节点的指针。

 

各种树结构对比

B树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点；

B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；

 

 

常见数据结构 

HASH表：通过HASH函数能快速定位数据，仅适用于等值查询，不适用于范围查询，查询时间复杂度为O(1)，更新时间复杂度为O(1)。
有序数组：通过二分法能快速定位数据，适用于等值查询和范围查询，但仅适用于静态数据，查询复杂度为O(1)，更新时间复杂度O(N)。
平衡搜索树：从N次(数层级)数节点扫描能快速定位数据，适用于等值查询和范围查询，查询时间复杂度为O(log(N))，更新时间复杂度为O(log(N))

 

LSM数

在一些存储日志或追求快速批量写入大量数据的NOSQL数据库中，可能会采用LSM数来存储数据，其设计思想为：

将对数据的修改增量保存在内存中，达到指定的大小限制后，将这些修改操作批量写入到磁盘，在读取时需要合并磁盘中的历史数据和内存中的最新数据，以牺牲读取性能来提升写入性能。

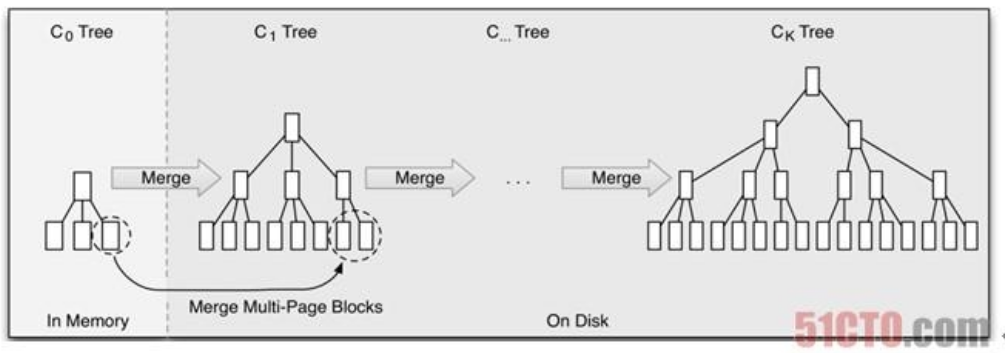
LSM树将数据拆分成N个单元，先将数据写入内存，然后将内存单元的数据刷新到磁盘，再定期对磁盘中的数据进行合并成树，以优化读性能。

==================================================

摘抄自：https://blog.csdn.net/zwz2011303359/article/details/63262541