数据结构与算法：二叉排序树

二叉排序树

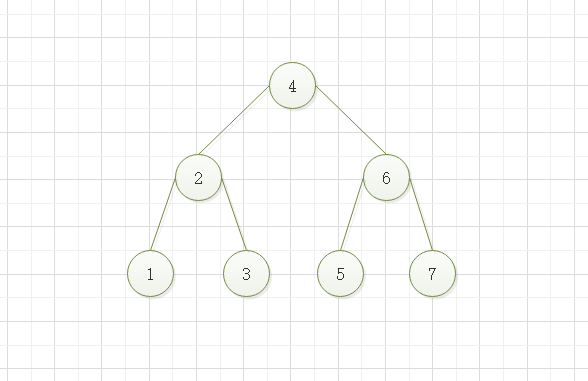
二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。是数据结构中的一类。在一般情况下，查询效率比链表结构要高。

二叉排序树的定义：

• 当左子树不为空时，左子树上的所有节点值都小于左子树的根节点值

• 当右子树不为空时，右子树上的所有节点值都小于右子树的根节点值

• 如果二叉树中有相同值节点时，可以放在它的左子节点或右子节点（如果不是开发需要，尽量不要有相同值的节点）

 

插入操作

步骤：

(1) 判断根节点是否为空，如果为空则将插入节点设置为根节点

(2.1) 判断插入节点值是否小于当前节点值，如果小于则往左节点走

(2.2) 当往左节点走时判断左节点是否为空，如为空则将左节点设置为插入节点，不为空则跳到步骤(2)

(3.1) 判断插入节点值是否大于当前节点值，如果大于则往右节点走

(3.2) 当往右节点走时判断右节点是否为空，如为空则将右节点设置为插入节点，不为空则跳到步骤(2)

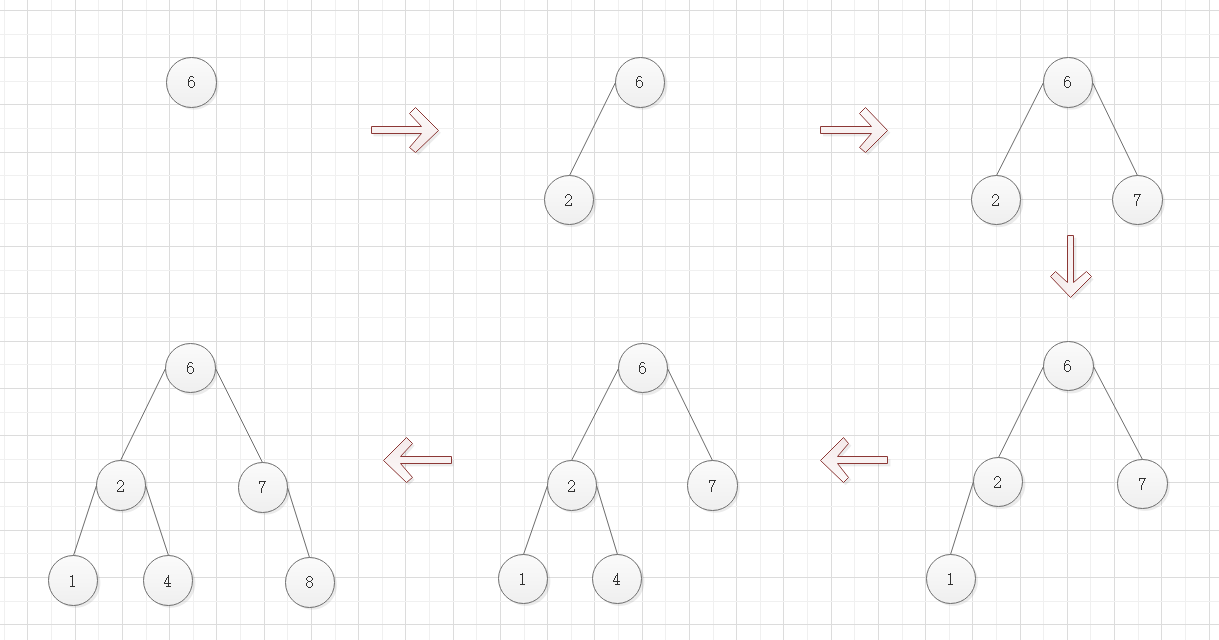
下图是将 [6, 2, 7, 1, 4, 8] 数组按顺序插入二叉排序树的过程图示：

代码实现

BSTNode root;//二叉排序树的根节点

public void add(BSTNode node){
    //如果根节点为空则，则将传入节点设置为根节点
    if (root == null){
        root = node;
    }else {
        add(node, root);
    }
}

/**
 * 在二叉排序树中添加节点
 * @param node 添加的节点
 * @param pointer 辅助指针节点，初始指向根节点
 */
public void add(BSTNode node, BSTNode pointer){
    if (node == null){
        return;
    }

    if (pointer.value > node.value){//指针节点值大于添加节点值时
        //如果指针节点的左节点刚好为空，则将添加节点插入到该左节点
        if (pointer.left == null){
            pointer.left = node;
        }else {
            //如果不是则继续往左节点走
            add(node, pointer.left);
        }
    }else {//指针节点值小于添加节点值时
        //如果指针节点的右节点刚好为空，则将添加节点插入到该右节点
        if (pointer.right == null){
            pointer.right = node;
        }else {
            //如果不是则继续往右节点走
            add(node, pointer.right);
        }
    }
}

 

查找操作

步骤：

(1) 判断当前节点是否是查找节点，如果是则直接返回当前节点

(2) 判断当前节点值是否大于查找节点值，如果大于则往左节点查找，跳到步骤(1)

(3) 判断当前节点值是否小于查找节点值，如果小于则往右节点查找，跳到步骤(1)

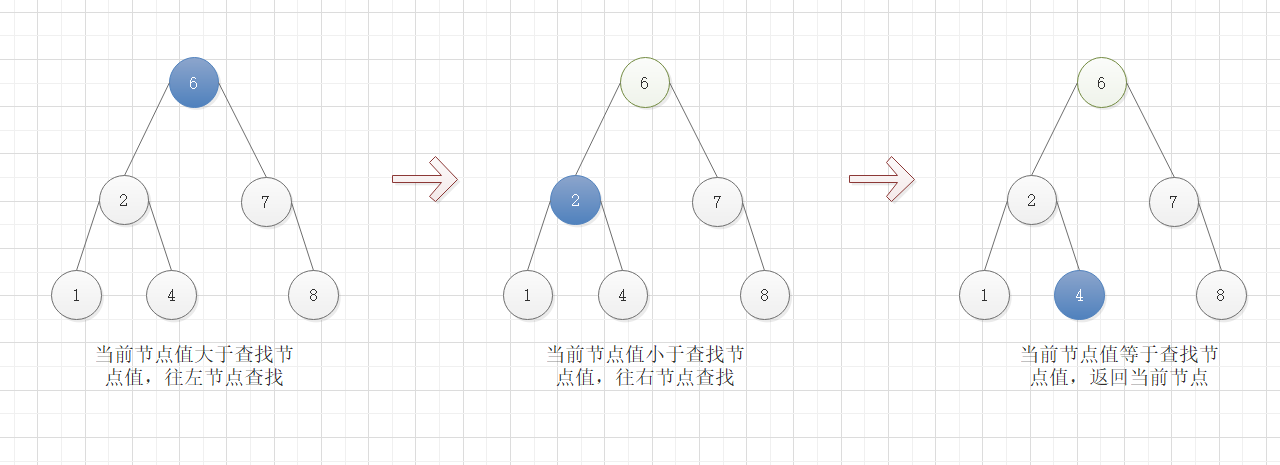
下图是从二叉排序树中查找值为4的节点的图示：

代码实现

//根据value值查找节点
public BSTNode searchNode(int value){
    if (root == null){
        return null;
    }
    return searchNode(value, root);
}

/**
 * 根据value值查找节点
 * @param value 查找的节点
 * @param node 查找的树
 * @return
 */
public BSTNode searchNode(int value, BSTNode node){
    //如果当前节点的值等于value时，则返回该节点
    if (node.value == value) {
        return node;
    } else if (node.value > value){//当前节点的值大于value时
        //如果该节点的左节点为空，则表示二叉排序树内没有该值的节点，返回空
        if (node.left == null)
            return null;
        //左节点不为空，继续往左子树查找
        return searchNode(value, node.left);
    }else {//当前节点的值小于value时
        //如果该节点的右节点为空，则表示二叉排序树内没有该值的节点，返回空
        if (node.right == null)
            return null;
        //右节点不为空，继续往右子树查找
        return searchNode(value, node.right);
    }
}

 

删除操作

删除节点可能有的3中状态：

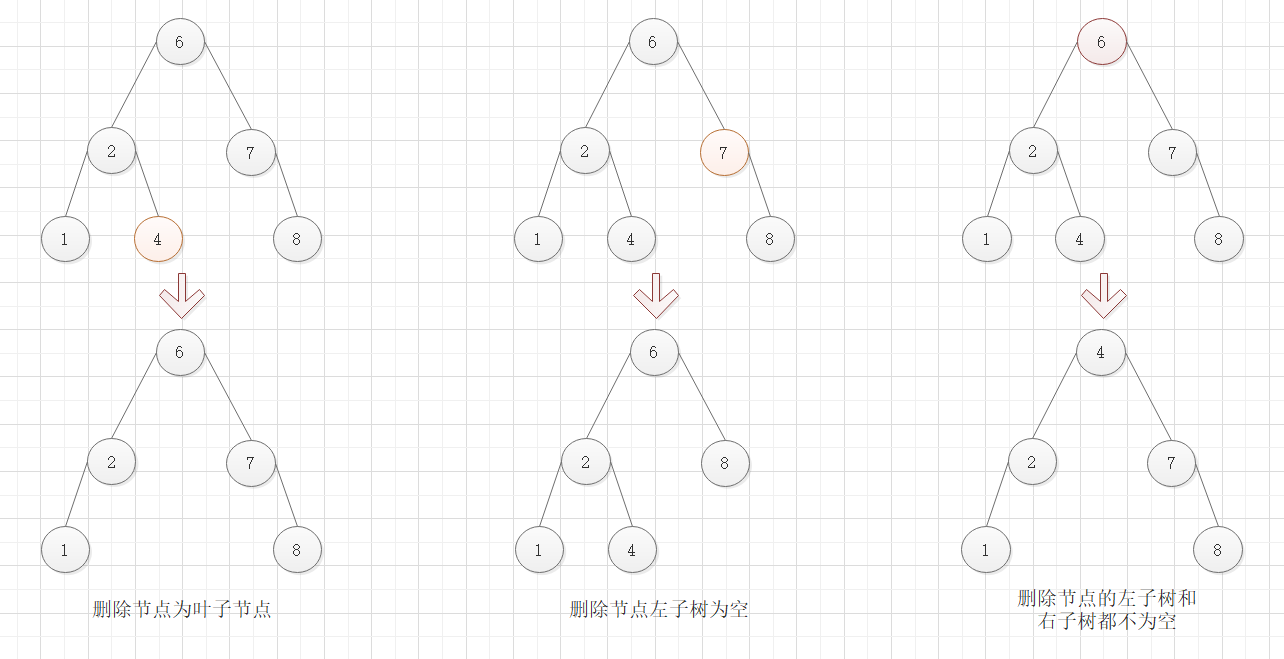
• 删除节点是叶子节点

• 删除节点只有左子树为空或右子树为空

• 删除节点左子树和右子树都为空

步骤：

(1) 判断删除节点值是否小于当前节点值，如小于则往左节点走

(2) 判断删除节点值是否大于当前节点值，如大于则往右节点走

(3) 当删除节点值等于当前节点值时，即当前节点时要删除的节点，判断当前节点是什么状态

(3.1) 当前节点是叶子节点时，则直接删除当前节点

(3.2) 当前节点左子树为空时，则将右节点顶上，代替当前节点位置

(3.3) 当前节点右子树为空时，则将左节点顶上，代替当前节点位置

(3.4) 当前节点左子树和右子树都不为空时，则将左子树的最大值节点取出后删除，再用最大值节点顶替当前节点位置

代码实现

/**
 * 根据value值删除节点
 * 删除节点可能有的3种状态：
 * 1.该节点是叶子节点
 * 2.该节点只有左子树或只有右子树
 * 3.该节点左子树和右子树都有
 * @param value 要删除节点的value值
 */
public BSTNode delete(int value, BSTNode node){
    if (value < node.value){//当查找节点值小于当前节点值
        //向左子树递归遍历，并将删除后的新的左子树连接到左节点位置代替原先左子树
        node.left = delete(value, node.left);
        //返回删除后新的树
        return node;
    }else if(value > node.value){//当查找节点值大于当前节点值
        //向右子树递归遍历，并将删除后的新的右子树连接到右节点位置代替原先右子树
        node.right = delete(value, node.right);
        //返回删除后新的树
        return node;
    }else {//当查找节点值等于当前节点值时，即当前节点就是要删除的节点
        //删除节点时叶子节点的状态
        if (node.left == null && node.right == null){
            //直接将该节点设为空
            return null;
        }
        //删除节点左子树为空，右子树不为空的状态
        else if (node.left == null && node.right != null){
            //保存删除节点的右子树
            BSTNode rightSubTree = node.right;
            //将删除节点的右子树设为空，使得该节点能够尽早被垃圾回收
            node.right = null;
            //返回删除节点的右子树，连接到删除节点的父节点
            return rightSubTree;
        }
        //删除节点右子树为空，左子树不为空的状态
        else if (node.right == null && node.left != null){
            BSTNode leftSubTree = node.left;
            node.left = null;
            return leftSubTree;
        }
        //删除节点的左子树和右子树都不为空的状态
        //这里我们使用的是左子树的最大值节点代替的方法
        else {
            //获取左子树的最大值节点并从左子树中删除它
            BSTNode max = max(node.left);
            //将该最大值节点的左子树和右子树设置为该节点的左子树和右子树
            max.left = delMax(node.left);
            max.right = node.right;
            //将删除节点的左子树和右子树设为空，使得该节点能够尽早被垃圾回收
            node.left = null;
            node.right = null;
            //执行完删除操作后，返回以最大值节点为根节点的新的树，连接的删除节点的父节点
            return max;
        }
    }
}

/**
 * 查找传入节点树下value值最大的节点并删除该节点
 * @param node
 * @return
 */
public BSTNode delMax(BSTNode node){
    if (node.right != null){
        node.right = delMax(node.right);
        return node;
    }else {
        BSTNode leftSubTree = node.left;
        node.left = null;
        return leftSubTree;
    }
}
/**
 * 查找传入节点树下value值最大的节点并放回该节点
 * 在二叉排序树中最大值的节点就是最右叶子节点
 * @param node
 * @return
 */
public BSTNode max(BSTNode node){
    BSTNode max = node;
    while (max.right != null){
        max = max.right;
    }
    return max;
}

 

完整代码

public class BinarySortTreeDemo {
    public static void main(String[] args) {
        int array[] = {13,7,8,3,29,6,1};
        BinarySortTree binarySortTree = new BinarySortTree();
        for (int i=0; i<array.length; i++){
            binarySortTree.add(new BSTNode(array[i]));
        }
        binarySortTree.midOrder();

        System.out.println("删除后二叉顺序树的节点：");
        binarySortTree.delete(13);
        binarySortTree.delete(7);
        binarySortTree.delete(1);
        binarySortTree.delete(29);
        binarySortTree.delete(6);

        binarySortTree.midOrder();
    }
}

//二叉排序树
class BinarySortTree{
    BSTNode root;

    public void setRoot(BSTNode root){
        this.root = root;
    }

    //添加节点
    public void add(BSTNode node){
        //如果根节点为空则，则将传入节点设置为根节点
        if (root == null){
            root = node;
        }else {
            add(node, root);
        }
    }

    /**
     * 在二叉排序树中添加节点
     * @param node 添加的节点
     * @param pointer 指针节点，初始指向根节点
     */
    public void add(BSTNode node, BSTNode pointer){
        if (node == null){
            return;
        }

        if (pointer.value > node.value){//指针节点值大于添加节点值时
            //如果指针节点的左节点刚好为空，则将添加节点插入到该左节点
            if (pointer.left == null){
                pointer.left = node;
            }else {
                //如果不是则继续往左节点走
                add(node, pointer.left);
            }
        }else {//指针节点值小于添加节点值时
            //如果指针节点的右节点刚好为空，则将添加节点插入到该右节点
            if (pointer.right == null){
                pointer.right = node;
            }else {
                //如果不是则继续往右节点走
                add(node, pointer.right);
            }
        }
    }

    //根据value值查找节点
    public BSTNode searchNode(int value){
        if (root == null){
            return null;
        }
        return searchNode(value, root);
    }

    /**
     * 根据value值查找节点
     * @param value 查找的节点
     * @param node 查找的树
     * @return
     */
    public BSTNode searchNode(int value, BSTNode node){
        //如果当前节点的值等于value时，则返回该节点
        if (node.value == value) {
            return node;
        } else if (node.value > value){//当前节点的值大于value时
            //如果该节点的左节点为空，则表示二叉排序树内没有该值的节点，返回空
            if (node.left == null)
                return null;
            //左节点不为空，继续往左子树查找
            return searchNode(value, node.left);
        }else {//当前节点的值小于value时
            //如果该节点的右节点为空，则表示二叉排序树内没有该值的节点，返回空
            if (node.right == null)
                return null;
            //右节点不为空，继续往右子树查找
            return searchNode(value, node.right);
        }
    }


    public void delete(int value){
        //判断删除节点在二叉排序树中是否存在
        BSTNode node = searchNode(value);
        if (node == null){
            throw new RuntimeException("二叉排序树内无对应节点");
        }
        //将删除后新的二叉排序树更换掉原先二叉排序树
        root = delete(value, root);
    }

    /**
     * 根据value值删除节点
     * 删除节点可能有的3种状态：
     * 1.该节点是叶子节点
     * 2.该节点只有左子树或只有右子树
     * 3.该节点左子树和右子树都有
     * @param value 要删除节点的value值
     */
    public BSTNode delete(int value, BSTNode node){
        if (value < node.value){//当查找节点值小于当前节点值
            //向左子树递归遍历，并将删除后的新的左子树连接到左节点位置代替原先左子树
            node.left = delete(value, node.left);
            //返回删除后新的树
            return node;
        }else if(value > node.value){//当查找节点值大于当前节点值
            //向右子树递归遍历，并将删除后的新的右子树连接到右节点位置代替原先右子树
            node.right = delete(value, node.right);
            //返回删除后新的树
            return node;
        }else {//当查找节点值等于当前节点值时，即当前节点就是要删除的节点
            //删除节点时叶子节点的状态
            if (node.left == null && node.right == null){
                //直接将该节点设为空
                return null;
            }
            //删除节点左子树为空，右子树不为空的状态
            else if (node.left == null && node.right != null){
                //保存删除节点的右子树
                BSTNode rightSubTree = node.right;
                //将删除节点的右子树设为空，使得该节点能够尽早被垃圾回收
                node.right = null;
                //返回删除节点的右子树，连接到删除节点的父节点
                return rightSubTree;
            }
            //删除节点右子树为空，左子树不为空的状态
            else if (node.right == null && node.left != null){
                BSTNode leftSubTree = node.left;
                node.left = null;
                return leftSubTree;
            }
            //删除节点的左子树和右子树都不为空的状态
            //这里我们使用的是左子树的最大值节点代替的方法
            else {
                //获取左子树的最大值节点并从左子树中删除它
                BSTNode max = max(node.left);
                //将该最大值节点的左子树和右子树设置为该节点的左子树和右子树
                max.left = delMax(node.left);
                max.right = node.right;
                //将删除节点的左子树和右子树设为空，使得该节点能够尽早被垃圾回收
                node.left = null;
                node.right = null;
                //执行完删除操作后，返回以最大值节点为根节点的新的树，连接的删除节点的父节点
                return max;
            }
        }
    }

    /**
     * 查找传入节点树下value值最大的节点并删除该节点
     * @param node
     * @return
     */
    public BSTNode delMax(BSTNode node){
        if (node.right != null){
            node.right = delMax(node.right);
            return node;
        }else {
            BSTNode leftSubTree = node.left;
            node.left = null;
            return leftSubTree;
        }
    }
    /**
     * 查找传入节点树下value值最大的节点并放回该节点
     * 在二叉排序树中最大值的节点就是最右叶子节点
     * @param node
     * @return
     */
    public BSTNode max(BSTNode node){
        BSTNode max = node;
        while (max.right != null){
            max = max.right;
        }
        return max;
    }

    public void midOrder(){
        if (root != null){
            midOrder(root);
        }else {
            System.out.println("二叉顺序树为空，无法遍历");
        }
    }

    //中序遍历
    public void midOrder(BSTNode node){
        if (node.left != null){
            midOrder(node.left);
        }
        System.out.println(this);
        if (node.right != null){
            midOrder(node.right);
        }
    }
}

//二叉排序树节点
class BSTNode{
    int value;
    BSTNode left;
    BSTNode right;

    public BSTNode(int value){
        this.value = value;
    }

    @Override
    public String toString() {
        return "BSTNode{" +
                "value=" + value +
                '}';
    }
}